|
|
Примеры параметрического способа уравнивания139.1. Уравнивание углов в полигоне
Задача решается с использованием исходных данных § 137, п. 137.1. Дополнительно известен дирекционный угол линии АВ (αАВ = 91° 47' 14,6"). Вообще говоря, если дирекционный угол исходной стороны неизвестен либо не может быть в настоящий момент определён, то в качестве исходного можно принять любое условное значение дирекционного угла любой стороны фигуры и выполнить уравнивание. Шаг 1. Общее число измерений n = 4, число необходимых измерений k = 3, число избыточных измерений r = 1. Шаг 2. Выбираем параметры tj (их число должно быть равно числу необходимых измерений, т.е. 3). В качестве параметров выбираем дирекционные углы сторон фигуры: t1 = αBC ; t2 = αСD; t3 = αDA . Шаг 3. Составляем параметрические уравнения, т.е. выражаем все измеренные величины через выбранные параметры tj:
Шаг 4. Находим приближённые значения tj0 параметров tj:
Шаг 5. В соответствии с функциями (14.147) находим коэффициенты aij и свободные члены li параметрических уравнений поправок νi :
Как видно, значение Wβ представляет собой угловую невязку в полигоне, т.е. в данном случае свободный член равен угловой невязке с обратным знаком. Поскольку Wβ = + 7", то l4 = - 7". Таблица 14.16 Матрица коэффициентов, свободных членов и весов
Составим таблицу (14.16) коэффициентов aij , свободных членов li и весов pi измеренных величин. Шаг 6. Составим и решим систему нормальных уравнений поправок τj. Запишем уравнения поправок τj в развернутом виде в соответствии с параметрами, указанными в табл. 14.16:
После подстановки значений, приведенных в табл. 14.16, получим окончательный вид уравнений поправок τj:
Из решения системы уравнений (14.151) получим: τ 1 = +1,15"; τ2 = +2,27"; τ3 = -2,39" Шаг 7. Вычисляем значения поправок τ j с округлением до 0,1":
Контроль: сумма поправок равна невязке с обратным знаком. Сравните полученные значения поправок с поправками, полученными в коррелатном способе уравнивания (п. 137.1). Дальнейшие вычисления сводятся к определению уравненных значений параметров tj по формуле (14.138), а также к вычислению уравненных значений измеренных углов по формуле (14.136).
139.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками
При объяснении решения задачи уравнивания системы нивелирных ходов с несколькими узловыми точками параметрическим способом используем исходные данные § 137, п. 137.2. Далее не будем обозначать пошаговым способом алгоритм решения задачи, но сохраним ту же последовательность действий, как это и производилось выше в некоторых примерах. В качестве параметров tj выбираем высоты точек 1, 2, 3 и 4 (число параметров должно быть равно числу необходимых измерений, т.е. 4): t 1 = Н1 ; t2 = Н2 ; t3 = Н3; t 4 = Н4. Составим параметрические уравнения связи, т.е. выразим измеренные величины через функции выбранных параметров:
Найдем приближённые значения выбранных параметров (задачу решим без предварительного уравнивания системы нивелирных ходов):
В соответствии с функциями (14.153) находим коэффициенты aij и свободные члены уравнений поправок. Свободные члены находим как невязки в уравнениях (14.153):
Составим матрицу коэффициентов, свободных членов и весов (табл. 14.17). По установленным выше правилам составим нормальные уравнения поправок с учётом данных, приведённых в табл. 14.17:
Из решения системы линейных уравнений (14.154) находим: τ 1 = - 1,700; τ2 = + 1,466; τ3 = - 4,672; τ 4 = +10,026.
Таблица 14.17 Матрица коэффициентов, свободных членов и весов
Вычисляем значения поправок в превышения, предварительно составив уравнения поправок, исходя из табл. 14.17:
Не будем проводить дальнейшие вычисления, поскольку их результаты будут такими же, как и в примере уравнивания данной системы нивелирных ходов коррелатным способом (сравните поправки в превышения в том и другом способах). Но это делается только с целью сокращения объёма учебника. Вам же во всех задачах необходимо выполнять полный контроль результатов уравнивания, т. е. необходимо полностью убедиться в правильности решения задачи. Вы можете самостоятельно проверить уравненные значения выбранных в этом примере параметров (высот точек 1, 2, 3 и 4) суммированием их приближённых значений с соответствующими поправками τj. Например, Н1 = 81922 – 1,700 = 81920 мм = 81,920 м.
139.3. Уравнивание системы полигонометрических ходов с двумя узловыми точками
При решении задачи уравнивания систем полигонометрических ходов с одной или несколькими узловыми точками устанавливают число независимых полигонометрических ходов, включающих данные узловые точки и узловые линии. Для каждого из выбранных ходов составляют три уравнения поправок: одно уравнение – по условию суммы горизонтальных углов; два уравнения характеризуют условия координат (для координат х и координат у). Решение указанной задачи рассмотрим на примере системы полигонометрических ходов с теми же исходными данными (раздел 137.3). Шаг 1.Общее число измерений n = 19, число необходимых измерений k = 10, число избыточных измерений r = 9. Шаг 2. Выбор параметров tj. В качестве параметров tj выбираем координаты точек 1, 2, 3, М и N: x1 = t1, y1 = t2 ; x2 = t3, y2 = t4 ; x3 = t5 , y3 = t6 ; xM = t7 , yM = t8 ; xN = t9 , yN = t10 . Шаг. 3. Выражение измеренных величин через выбранные параметры по аналогии с формулами (14.153). Для этого примем для расчётов три независимых полигонометрических хода: (1): А-В-1-M-F-E; (2): A-B-1-M-N-2-C-D; (3): H-G-3-N-2-C-D (как и при уравнивании коррелатным способом). Предлагаем самостоятельно составить соответствующие формулы на основе пояснений для формул (14.105) – (14.132). Шаг 4. Определение приближённых значений tj0 параметров tj.
Таблица 14.18 Предварительная обработка ведомости координат
Для этого по каждому из ходов выполним расчёты (см. в табл. 14.18), но с использованием способа раздельного уравнивания как это выполняется при обработке разомкнутого теодолитного хода (гл. 7). Приближённые значения параметров из уравнивания раздельным способом проведены в табл. 14.19. Таблица 14.19
Шаг 5. Приведение функций взаимосвязи измеренных величин к линейному виду, вычисление коэффициентов a и b и свободных членов l уравнений поправок. Запишем уравнения поправок в измеренные величины с учётом того, что погрешности исходных данных приняты нами равными нулю. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. Пользуясь таблицами 14.18 и 14.19, найдем из решения обратных геодезических задач предварительные значения дирекционных углов и расстояний (табл. 14.20). Таблица 14.20
Вычислим коэффициенты условных уравнений поправок по формулам (14.111) и (14.112) – табл. 14.21. Таблица 14.21
Получим значения свободных членов: для угловых поправок – в секундах; для поправок в расстояния – в дециметрах. Свободные члены для уравнений поправок в углы найдём как разницу вычисленного горизонтального угла в точке (с использованием предварительных значений дирекционных углов (табл. 14.20)) и измеренным его значением. Свободные члены в уравнения поправок в расстояния определим как разность предварительного значения расстояния (табл. 14.20) и измеренного его значения. (Аналогичные вычисления производятся и в случае обработки одиночного полигонометрического хода). Значения полученных поправок приведены в табл. 14.22. Табл. 14.22
C учётом коэффициентов (табл. 14.21) и свободных членов (табл. 14.22) уравнения поправок (14.156) примут вид: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. Составим матрицу коэффициентов, свободных членов и весов для получения коэффициентов уравнений поправок (табл. 14.23).
Таблица 14.23
Шаг 6. Составление и решение нормальных уравнений параметрических поправок. В результате обработки табл. 14.23 получим систему нормальных уравнений поправок к выбранным параметрам:
Из решения системы линейных уравнений одним из известных способов получим:
Шаг 7. Вычисление поправок, уравненных значений измеренных величин и контроль уравнивания. Вычислим по формулам (14.157) значения поправок в измеренные величины (табл. 14.24). Таблица 14.24
Здесь необходимо выполнить предварительный контроль вычисления поправок в углы: сумма поправок по данному полигонометрическому ходу должна быть равна невязке этого хода с обратным знаком. Допустимы расхождения в пределах погрешностей округлений. В примере имеются расхождения до 0,1" (проверьте по суммам соответствующих поправок). Далее введём поправки в предварительные значения параметров (координат точек), т.е. выполним окончательное уравнивание координат (табл. 14.25). Для этого к значениям координат табл. 14.19 следует прибавить соответствующие поправки (14.159). Таблица 14.25
Используя данные табл. 14.25 и таблицы координат исходных точек, вычислить уравненные значения дирекционных углов и расстояний (таблица уравненных значений дирекционных углов и расстояний подобна табл. 14.20). Далее необходимо проверить качество уравнивания всех горизонтальных углов и расстояний по следующей схеме: - вычислить разность уравненных дирекционных углов направлений, образующих угол ( αB1 – αBA = 117o23'40,4" – 251o08'14,3" = 226o15'26,1"); - вычислить уравненное значение угла, т.е. к измеренному значению угла прибавить полученную поправку (β1' = 226о15'25,0" + 1,1" = =226о15'26,1"); как видим, разница контрольного угла и уравненного его значения получились одинаковыми в пределах погрешности округлений; - вычислить уравненное зачение расстояния как сумму измеренного расстояния и поправки в него, полученной в табл. 14.24 (s1' = 475,8850 - 0,026= =475,8824 м); из решения обратной геодезической задачи получено такое же значение (разности могут быть также в пределах округлений). Указанные вычисления следует выполнить для всех измеренных и уравненных элементов. После контроля необходимо выполнить обработку полигонометрических ходов с использованием значений уравненных элементов.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ; (14.147)
; (14.147)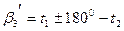 ;
; .
. (14.148)
(14.148)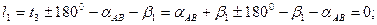
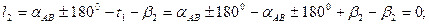
 (14.149)
(14.149)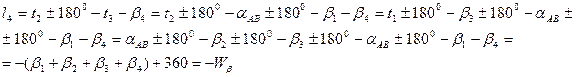
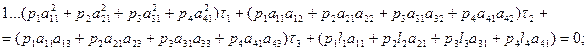
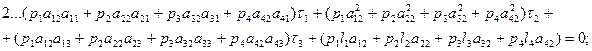
 (14.150)
(14.150) (14.151)
(14.151)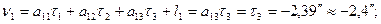
 (14.152)
(14.152)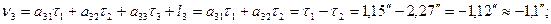
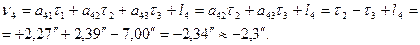
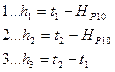
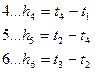 (14.153)
(14.153)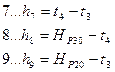
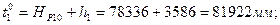
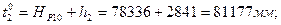
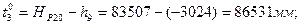
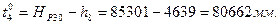
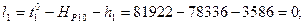
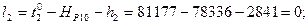
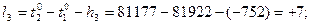
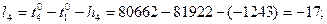
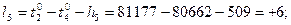
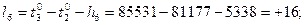

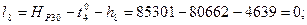
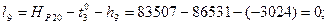
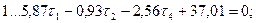
 (14.154)
(14.154)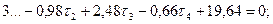
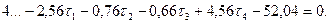

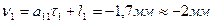
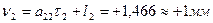
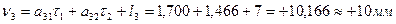
 (14.155)
(14.155)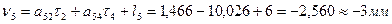
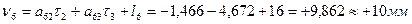
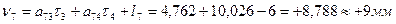
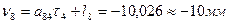
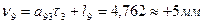
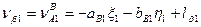
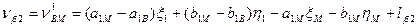
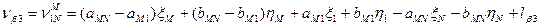
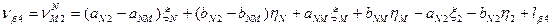
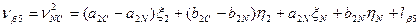
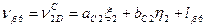
 (14.156)
(14.156)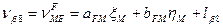
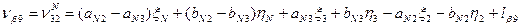
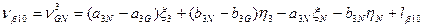
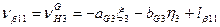
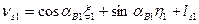
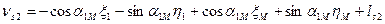
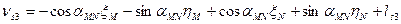

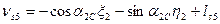
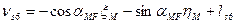
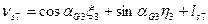
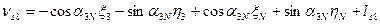
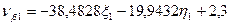
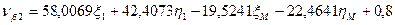
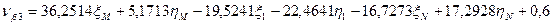
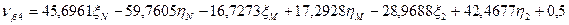
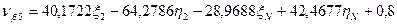
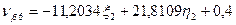
 (14.157)
(14.157)
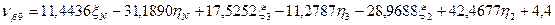

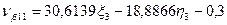
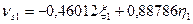
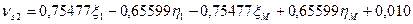
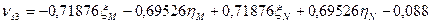
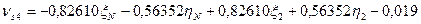
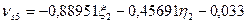
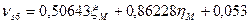
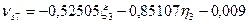

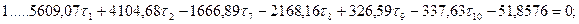
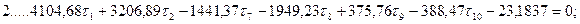
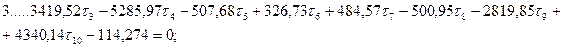
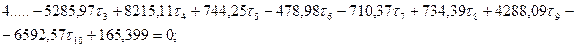
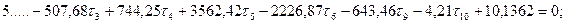
 (14.158)
(14.158)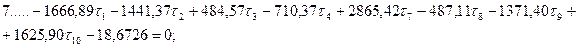
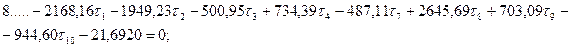

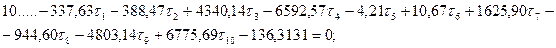
 ;
;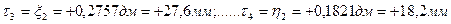
 (14.159)
(14.159)