
|
|
Основные источники погрешностей геометрического нивелированияНа точность определения превышений влияют многочисленные факторы, среди которых основными являются: влияние кривизны Земли и рефракции атмосферы; невыполнение главного условия нивелира; погрешности отсчётов по шкалам реек; погрешности установки зрительной трубы; погрешности в нанесении делений шкал реек и др. Рассмотрим влияние указанных погрешностей и факторов на точность нивелирования. 1. Влияние кривизны Земли. На физической поверхности Земли на расстоянии L находятся точки А и В, превышение между которыми равно h (рис. 6.3). Установим нивелир точно посредине между точками А и В и возьмём отсчёты по рейкам, полагая, что световой луч (1) в направлении визирной оси распространяется в атмосфере прямолинейно. Для правильных отсчётов по рейкам следовало бы потребовать, чтобы световой луч проходил по уровенной поверхности, определяемой высотой прибора, т.е. по пути (2). В этом случае превышение между точками будет соответствовать истинному его значению: hист = З2 – П2 . (6.13) На самом деле мы имеем h1 = З1 – П1 . (6.14) Очевидно, что для симметричной схемы погрешности в отсчётах по рейкам ∆З1 = З1 – З2 и ∆П1 = П1 – П2 , определяемые влиянием кривизны Земли, будут одинаковыми, поскольку LA = LB. Следовательно,
При нивелировании вперёд (рис. 6.3б) ∆З1 значительно меньше ∆П1, в связи с чем погрешность ∆П1 практически полностью входит в значение измеренного превышения. Величина погрешности k из-за кривизны Земли в отсчёте по рейке, находящейся на расстоянии L от нивелира, может быть оценена по формуле
где R – радиус Земли.
Рис. 6.3. Погрешности нивелирования из-за влияния кривизны Земли, рефракции и невыполнения главного условия нивелира.
Указанная погрешность при нивелировании может быть определена практически с любой точностью с учётом эллиптичности Земли, т.е. с учётом параметров референц-эллипсоида Красовского. Данные вопросы рассматриваются подробно в курсе высшей геодезии. 2. Влияние рефракции атмосферы. Визирные лучи (3), проходя в атмосфере через слои воздуха, имеющие разную плотность, искривляются, отклоняясь в сторону земной поверхности. Погрешность в отсчёте, вызванная влиянием рефракции атмосферы, r = (З3 – З2 ), r = (П3 – П2), может быть оценена по приближённой формуле
Если условия измерений стабильны для визирных лучей в направлениях А и В, то можно полагать, что при симметричной схеме измерений погрешность из-за рефракции атмосферы исключается в разности отсчётов, как и при влиянии кривизны Земли. Однако практически в указанных направлениях рефракция может оказаться различной, в связи с чем возникает погрешность, которую практически невозможно учесть в измеренном превышении. При высокоточных измерениях, например, для ослабления указанной погрешности нивелирование выполняют в утренние и вечерние часы, когда рефракция атмосферы минимальная и стабильная. Часто погрешности k и r объединяют и определяют общую погрешность влияния кривизны Земли и рефракции
Приведём в качестве сравнительных характеристик значения погрешностей k и r и суммарной погрешности f (мм) для радиуса Земли R = =6371,11 км и различных расстояний L(м) от нивелира до рейки (табл. 6.1).
Таблица 6.1
Как видно из этой таблицы, уже при расстояниях 100 м погрешность из-за влияния кривизны Земли составляет почти 0,8 мм. Погрешность из-за влияния рефракции атмосферы имеет знак, обратный знаку погрешности из-за кривизны Земли, в связи с чем общая погрешность отклонения отсчёта от истинного меньше, чем k. При нивелировании из середины (при симметричной схеме) rЗ = rП , т.е. эти погрешности исключаются из значения полученного превышения, а при нивелировании вперёд rЗ значительно меньше rП, что приводит к погрешности в определении превышения. 3. Невыполнение главного условия нивелира. Если в нивелире не выполняется главное условие, т.е. после установки нивелира в рабочее положение визирный луч (4) займет не горизонтальное положение, а будет отклонен от него на угол i, то отсчёты по рейкам будут равны З4 и П4. Разности отсчётов (З4 – З1) и (П4 – П1) характеризуют погрешность из-за невыполнения главного условия нивелира. Её величина может быть оценена по формуле
где ρ = 206265". При нивелировании из середины, при использовании симметричной схемы измерений, погрешности в отсчётах по рейкам из-за невыполнения главного условия нивелира будут одинаковыми и исключатся в разности отсчётов. При нивелировании вперёд превышение будет содержать систематическую погрешность, если визирная ось зрительной трубы не будет при измерениях совпадать с горизонтальной плоскостью. Суммируя сказанное, сделаем следующий вывод: при нивелировании из середины влиянием кривизны Земли, рефракцией атмосферы, остаточным невыполнением главного условия нивелира, как систематическими погрешностями, можно пренебречь (при соблюдении требований установленной методики измерений). Вообще говоря, при любом неравенстве плеч на станции, если остаточная погрешность в превышении будет больше установленного допуска, схему измерений следует характеризовать как нивелирование вперёд. Рассмотрим пример оценки влияния погрешностей k, r и u на результат измерения превышения.
Пример 6.1.Оценка влияния кривизны Земли, рефракции атмосферы и невыполнения главного условия нивелира на результаты измерения превышений при разных плечах на станции. Исходные данные. Предположим, что точки А и В находятся на расстоянии 100 м (200 м) друг от друга. Неравенство плеч на станции равно 20 м (LA = 40 м (90 м); LB = 60 м (110 м)). Угол i = 10". Заданная точность определения превышения mh = 1 мм. Требуется оценить возможность обеспечения указанной точности измерений при данном неравенстве плеч. Решение.В скобках будут приведены результаты вычислений для расстояния между точками в 200 м. По формуле (6.16)
По формуле (6.17)
По формуле (6.19)
Как следует из результатов оценки, при разности плеч в 20 м (расстояниях между точками до 200 м) практически можно пренебречь влиянием рефракции атмосферы, влияние кривизны Земли можно считать пренебрегаемо малым, а вот невыполнение главного условия нивелира вызывает погрешность того же порядка, что и заданная точность измерения превышения. В таких случаях необходимо оценить допустимую величину разности плеч на станции, при которой погрешность из-за невыполнения главного условия составляла бы 1:3 ... 1:5 от заданной точности (допустимой погрешности) измерений, т.е. была бы пренебрегаемо малой. Примем ∆u = 0,2mh = 0,2 мм. Тогда
Очевидно, что при такой разности плеч погрешности из-за влияния кривизны Земли и рефракции атмосферы практически будут равны нулю.
4. Погрешность установки зрительной трубы. Данная погрешность обусловлена неточностью установки пузырька цилиндрического уровня в нульпункте, а также недостаточной чувствительностью уровня к малым перемещениям трубы элевационным винтом. Здесь же следует указать и на недостаточную чувствительность компенсатора у нивелиров с компенсатором (погрешность недокомпенсации). Принимая погрешность установки пузырька уровня mτ = 2" (для контактных уровней), расстояние от нивелира до реек L = 100 м, определим значение вероятной погрешности в отсчёте
Для превышения, определяемого разностью отсчётов, как это следует из фомулы погрешности для разности двойных измерений либо для функции, представленной разностью аргументов, ∆h(τ) = 5. Погрешность отсчёта по рейке - mтр. Указанная погрешность определяется недостаточной разрешающей способностью зрительной трубы нивелира:
где Гх – увеличение зрительной трубы. Предположим, что для тех же условий измерений Гх = 25х. Тогда mтр = 1,16 мм, а для превышения ∆h(тр) = 6. Погрешность в отсчёте из-за наклона рейки. Очевидно, что чем больше наклон рейки, тем больше будет и погрешность отсчёта. Предположим, что рейка отклонилась от вертикального положения на угол α (рис. 6.4). Визирный луч находится на высоте ао, соответствующей вертикальному положению рейки. Из-за наклона по рейке читается отсчёт а. Погрешность из-за наклона рейки может быть получена по формуле
При точном и высокоточном нивелировании используют нивелирные рейки, снабжённые круглым или цилиндрическим уровнем. В этом случае реечник удерживает рейку или закрепляет её в вертикальном положении по показанию уровня. 7. Погрешность в дециметровых делениях рейки - ∆д. Используемые при техническом нивелировании нивелирные рейки могут иметь погрешности в дециметровых делениях шкал до 0,7 мм, что допускается технической инструкцией. Для превышения, определяемого по различным дециметровым диапазонам, погрешность может составить ∆hд = 1 мм для реек, используемых для технического нивелирования. 8. Погрешнсоть округления отсчёта. Эта погрешность оценивается как 0,1 часть наименьшего деления рейки. То есть, если используется рейка с сантиметровыми делениями, то погрешность округления составит 1 мм, а для измеренного превышения ∆hо = =1,41 мм. Таким образом, ориентируясь на указанные основные погрешности 4 - 8, оценим вероятную погрешность определения превышения на станции технического нивелирования при плечах, равных 100 м (расстояние между точками – 200 м): Следует отметить, что анализ указанных погрешностей был выполнен применительно к техническому нивелированию. Однако примерно такой же анализ можно сделать и для точного и высокоточного нивелирования, для которых установлены соответствующие допуски на величину невыполнения главного условия, на разность плеч на станции геометрического нивелирования, на допустимую погрешность отсчёта по рейке и др.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (6.15)
. (6.15) , (6.16)
, (6.16)
 . (6.17)
. (6.17) . (6.18)
. (6.18) , (6.19)
, (6.19) мм; (0,31 мм).
мм; (0,31 мм). мм; (0,04 мм).
мм; (0,04 мм). мм; (0,97 мм).
мм; (0,97 мм). м.
м.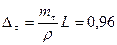 мм . (6.20)
мм . (6.20) ∙0,96 мм = 1,35 мм.
∙0,96 мм = 1,35 мм. , (8.21)
, (8.21) , (6.22)
, (6.22) Рис. 6.4. Влияние наклона рейки на точность отсчета.
Рис. 6.4. Влияние наклона рейки на точность отсчета.
 . (6.23)
Предположим, что α = 1о (ρ = 57,3о), ао = 2000 мм. Тогда ∆hH = 0,43 мм.
Для частичного устранения погрешности, возникающей из-за наклона рейки, при техническом нивелировании и нивелировании средней точности при больших отсчётах по рейке, реечник выполняет качание рейкой в направлении наблюдателя с переходом через вертикальное положение. Наблюдатель при этом фиксирует минимальный отсчет.
. (6.23)
Предположим, что α = 1о (ρ = 57,3о), ао = 2000 мм. Тогда ∆hH = 0,43 мм.
Для частичного устранения погрешности, возникающей из-за наклона рейки, при техническом нивелировании и нивелировании средней точности при больших отсчётах по рейке, реечник выполняет качание рейкой в направлении наблюдателя с переходом через вертикальное положение. Наблюдатель при этом фиксирует минимальный отсчет.
 мм . (6.24)
мм . (6.24)