
|
|
Вычисление площади поверхности
Понятие двойного интеграла можно использовать для определения площадей не только плоских фигур, но и кривых поверхностей. Пусть требуется вычислить площадь поверхности, ограниченной линией G; поверхность задана уравнением z=¦(x,y), где функция ¦(x,y) непрерывна и имеет непрерывные частные производные. Обозначим проекцию линии G на плоскость OXY через L. Область на плоскости OXY, ограниченную линией L, обозначим через D.
Разобьем произвольным образом область D на n элементарных площадок Ds1, Ds2¼Dsn . В каждой площадке Dsi возьмем точку Точке
Через точку
На этой плоскости выделим такую площадку Dsi, которая проектируется на плоскость OXY в виде площадки Dsi. Рассмотрим сумму всех площадок
Предел s этой суммы, когда наибольший из диаметров площадок Dsi стремится к нулю, называется площадью поверхности, т.е. по определению положим:
Угол gi есть в то же время угол между осью OZ и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеет:
Следовательно,
Подставляя это выражение в формулу (2), получим:
Так как предел интегральной суммы, стоящей в правой части последнего равенства, представляет собой, по определению, двойной интеграл
Это и есть формула, по которой вычисляется площадь поверхности z=¦(x,y). Замечание. Если уравнение поверхности дано в виде x=m(y,z) или y=X(x,z), то соответствующие формулы для вычисления поверхности имеют вид
где D’ и D'' – область на плоскостях OYZ и OXZ, в которых проектируется данная поверхность. Пример 1
(Площадь области s равна разности площадей прямоугольных треугольников).
Вычислить площадь части параболоида x²+y²=z, x²+y²=1 по формуле: найдем
где s - круг x²+y²£1 в плоскости XOY
Механическое приложение двойного интеграла Масса плоской фигуры
Пусть в области s распределено некоторое вещество, так что на каждую единицу площади области s приходится определенное количество этого вещества. Рассмотрим произвольную площадку Dsi области s. Пусть масса вещества, приходящаяся на данную площадку, есть Dm. Тогда Пусть Ds уменьшается, стягиваясь к точке
таким образом, поверхностная плотность есть функция ¦(x,y) координат точек области Обратно, пусть задана поверхностная плотность некоторого вещества как некоторая непрерывная функция ¦(Р)=¦ Разобьем область s на n частей Ds1, Ds2¼Dsn и в каждой Dsi возьмем точку Произведение ¦ Но это есть интегральная сумма для функции ¦ Пусть Dsi ®0, тогда предел этой интегральной суммы
Таким образом Получили механический смысл двойного интеграла от непрерывной, неотрицательной функции. Пример 3
z = x2+y2; z = 9 х = 2; х = -2; у =2; у = -2 Вычислим вначале объем болванки
Масса этой болванки будет равна

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
. будет соответствовать на поверхности точка
будет соответствовать на поверхности точка
 проведем касательную плоскость к поверхности. Уравнение ее имеет вид
проведем касательную плоскость к поверхности. Уравнение ее имеет вид (1)
(1) :
:
 (2)
(2) Вычислим площадь поверхности. Обозначим через gi угол между касательной плоскостью и плоскостью OXY. На основании известной формулы аналитической геометрии можно написать:
Вычислим площадь поверхности. Обозначим через gi угол между касательной плоскостью и плоскостью OXY. На основании известной формулы аналитической геометрии можно написать: или
или 

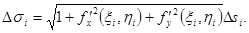

 то окончательно получаем:
то окончательно получаем:


 Найти площадь части конической поверхности
Найти площадь части конической поверхности  вырезаемой плоскостями x=0, y=0, x+y=1, x+y=2 и лежащей в I октанте.
вырезаемой плоскостями x=0, y=0, x+y=1, x+y=2 и лежащей в I октанте.
 т.е.
т.е.
 Пример 2
Пример 2
 то
то =
= 

 называется средней поверхностной плотностью вещества в области s.
называется средней поверхностной плотностью вещества в области s. , если этот предел существует, то он зависит от положения точки
, если этот предел существует, то он зависит от положения точки  и представляет некоторую функцию ¦(Pi) точки Р. Будем называть этот предел поверхностной плотностью вещества в точке Р.
и представляет некоторую функцию ¦(Pi) точки Р. Будем называть этот предел поверхностной плотностью вещества в точке Р.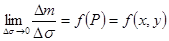

 численно равен массе плоской материальной области s, если плотность распределения массы в этой области равна подынтегральной функции ¦(x,y).
численно равен массе плоской материальной области s, если плотность распределения массы в этой области равна подынтегральной функции ¦(x,y). Вычислить массу болванки, отлитой из чугуна, если она ограничена поверхностями:
Вычислить массу болванки, отлитой из чугуна, если она ограничена поверхностями:
