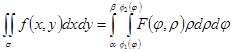|
|
Двойной интеграл в полярных координатах
Пусть область s ограничена кривыми Ф1(j)= r, Ф2( j)=r и лучами j=a, j=b, Ф2>Ф1,b>a Пусть в области задана непрерывная функция Z=F(j,r). Разобьем область s на части Ds1,Ds2¼Dsn . Составим интегральную сумму:
Из теоремы существования двойного интеграла следует, что при l®0 предел интегральной суммы равен по определению двойному интегралу от функции F(j,r) по области s
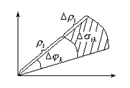
Вычислим этот двойной интеграл; так как предел этой суммы не зависит от способа разбиения области s на части Dsк, то разобьем область s с помощью лучей: j=j0, j=j1, ¼j=jn (j0=a, jn=b, j0<j1<¼<jn) и концентрических окружностей r=r0, r=r1,¼r=rm r0 равно наименьшему значению Ф1(j), причем rm равно наибольшему Ф2 (j) Пусть Dsik- область ограниченная линиями r=ri-1, r=ri, j=jk-1,j=jk Интегральная сумма:
где Pik – любая точка области Dsik
Площадь Dsik равна разности площадей двух секторов:
или
где ri<ri*<ri+Dri . Таким образом интегральная сумма имеет вид
где Пусть Dri®0, а Djк=const, тогда выражение в квадратных скобках принимает вид:
Пусть Djк®0 , тогда
Пусть требуется вычислить так как
тогда
x=rcosj, y=rsinj
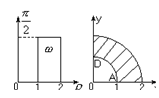
где w - область площади r0j, образом которой является данная четверть кольца. При отображении дуге АD окружности x²+y²=1 соответствует отрезок прямой а дуге ВС окружности x²+y²=4 –соответствует отрезок прямой Область w представляет собой прямоугольник: {1£r£2, 0£j£p¤2} в плоскости r0j.
Замена переменных в двойных интегралах
Расмотрим на них две области: s и w. Пусть функции устанавливают взаимнооднозначное соответствие между точками этих областей. Это значит, что каждой точке (u0,v0) из области w соответствуют точки (x0,y0) из области s, называемая образом точки (u0,v0), где x0=j(u0,v0), y0=y(u0,v0) И наоборот: (x0,y0)® (u0,v0), u,v – криволинейные координаты. Будем говорить, что Пусть функции
будет функцией Рассмотрим
Образы этих кривых на плоскости XOY, в свою очередь будут кусочно-гладкими и разобьют область s на n частей: Ds1, Ds2¼Dsn. Площади соответствующих областей Dwi и Dsi связаны соотношением
где М(mi,ni) –точки области Dwi. I(mi,ni) – якобиан отображения (6) в этой точке. Обозначим через Для получения разбиения области s на части Ds1, Ds2¼Dsn и специального выбора точек Р1, Р2¼Рn, составляет на этих частях интегральную сумму для двойного интеграла (7):
По построению имеем
которая является интегральной суммой для двойного интеграла по области w от непрерывной функции При lw®0 в области w, ls®0 в области s переходя к пределу в интегральной сумме имеем:
Данная формула есть формула замены переменных в двойных интегралах. Замечание Переход от прямоугольных координат к полярным является частным случаем (9): здесь u=j, v=r, x=rcosj, y=rsinj:
Следовательно

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
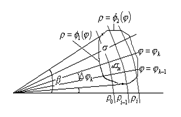 Пусть в полярной системе координат j,r задана область s такая, что каждый луч, проходящий через внутреннюю точку области пересекает границу области s не более чем в двух точках.
Пусть в полярной системе координат j,r задана область s такая, что каждый луч, проходящий через внутреннюю точку области пересекает границу области s не более чем в двух точках.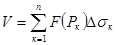
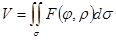
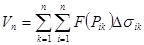
 (SS означает, что вначале мы суммируем по i, считая k=const т.е. отбираем все слагаемые, соответствующие областям, заключенным между двумя соседними лучами, а потом собираем все суммы по k)
(SS означает, что вначале мы суммируем по i, считая k=const т.е. отбираем все слагаемые, соответствующие областям, заключенным между двумя соседними лучами, а потом собираем все суммы по k)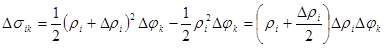
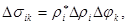

 - точка области Dsik
- точка области Dsik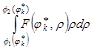
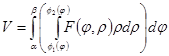
 область s задана в полярной системе координат, тогда вычисление двойного интеграла можно свести к повторному в полярных координатах,
область s задана в полярной системе координат, тогда вычисление двойного интеграла можно свести к повторному в полярных координатах,
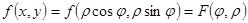
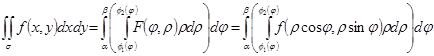 Пример. Вычислить
Пример. Вычислить  по четверти кольца 1£x²+y²£4, лежащего в I квадранте. Сделаем замену:
по четверти кольца 1£x²+y²£4, лежащего в I квадранте. Сделаем замену:
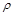 =1, 0£j£p¤2;
=1, 0£j£p¤2;
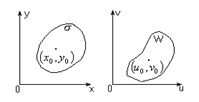 Пусть даны две плоскости с выбранными декартовыми системами координат UOV,XOY.
Пусть даны две плоскости с выбранными декартовыми системами координат UOV,XOY.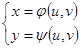 (6)
(6)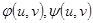 непрерывны в области W со своими частными производными первого порядка. Тогда определитель
непрерывны в области W со своими частными производными первого порядка. Тогда определитель
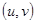 , определенной в области W. Этот функциональный определитель, называется определителем Якоби, или якобианом отображения (6)
, определенной в области W. Этот функциональный определитель, называется определителем Якоби, или якобианом отображения (6) (7)
(7)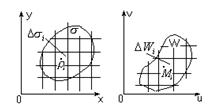 Заменим (7) равным ему двойным интегралом по переменным u,v по области w. Разобьем область w на n областей Dw1,Dw2¼Dwn с помощью кусочно-гладких кривых.
Заменим (7) равным ему двойным интегралом по переменным u,v по области w. Разобьем область w на n областей Dw1,Dw2¼Dwn с помощью кусочно-гладких кривых.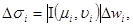
 образ точки М(mi,ni) при отображении (6).
образ точки М(mi,ni) при отображении (6).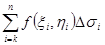
 ,
,
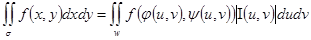

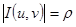 , поэтому:
, поэтому: