
|
|
Вычисление объема цилиндрического тела.Объем цилиндрического тела, имеющего основание в плоскости
Если цилиндрическое тело имеет основанием поверхность, которая не лежит в плоскости
ПРИМЕР 4.2. Вычислить объем тела, ограниченного поверхностями: РЕШЕНИЕ. Область D – треугольник, отсеченный от первой четверти координатной плоскости Получаем: 4.2.2. Вычисление площади плоской фигуры. Исходя из геометрической интерпретации двойного интеграла, площадь плоской фигуры численно равна объему прямого цилиндра с высотой, равной единице.
ПРИМЕР 4.3. Вычислить двойным интегралом площадь фигуры D, ограниченной линиями:
РЕШЕНИЕ. Строим линии и определяем область D. Линия Линия
параболы и прямой, решив систему
Выбираем порядок интегрирования.
Следовательно, разумно использовать интеграл вида (4.1.), иначе придется вычислять два повторных интеграла.
площадь фигуры D, ограниченной линиями 0 3 5
РЕШЕНИЕ. Строим линии, определяем фигуру. Видим, что она симметрична относительно оси
РЕШЕНИЕ. Строим линии. Определяем фигуру (рис.4.8.)и точки пересечения линий. Вычисляем составляющие формул (4.6.): По формулам (4.6.) получаем:
Приложение. ТАБЛИЦА ИНТЕГРАЛОВ. Интегралы, содержащие X = a2 + b2 1. 4. 8. Интегралы, содержащие X = a2- x2, X1 = x2- a2 10. 14. 16. Интегралы, содержащие X = ax2+bx+с. 19. 20. 21. Интегралы, содержащие sin x.
25. 27. 31. Интегралы, содержащие cos x. 32. 34. 38. Интегралы, содержащие cos x и sin x. 41. 43. Интегралы, содержащие tg x , ctg x. 45. 47. 49. Интегралы, содержащие, обратные тригонометрические функции. 51. 53. 54 56. Интегралы, содержащие показательные функции. 57. 61. Интегралы, содержащие логарифмические функции. 63. 65.
ЛИТЕРАТУРА. 1. Кремер Н.Ш. и др. Высшая математика для экономистов. - М.: Банки и биржи, ЮНИТИ, 1997. 2. Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Физматгиз, любое издание. 3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - М.: Физматгиз, Наука 1978. 4. Глаголев А.А., Солнцев Т.В. Курс высшей математики для студентов экономических специальностей вузов. - М.: Высшая школа, 1971. 5. Баврин Н.Н., Матросов В.А. Общий курс высшей математики. - М.: Наука,1986. 6.Зайцев И.А. Высшая математика. - М.: Высшая школа, 1991. 7. Щипачев В.С. Основы высшей математики. - М.: Высшая школа, 1994. 8. Выгодский М.Я. Справочник по высшей математике. - М.: Любое издание. 9. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч.1.- М.: Высшая школа, 1986. 10. Красс М.С. Математика для экономических специальностей. Учебник. М.: Высшее образование. ИНФРА - М, 1998. 11. Двайт Г.Б. Таблица интегралов и другие математические формулы. - М.: Наука, 1980.
СОДЕРЖАНИЕ. 1. Неопределенный интеграл …………………………………. 3 1.1. Определение и основные свойства неопределенного интеграла…...3 1.2. Непосредственное интегрирование………………………………….. 5 1.3. Интегрирование заменой переменной (метод подстановки)………..5 1.4. Интегрирование методом подведения под знак дифференциала…...6 1.5. Интегрирование по частям…………………………………………….7 1.6.Интегрирование функций, содержащих квадратный трёхчлен……...8 1.6.1. Квадратный трёхчлен находится в знаменателе дробной функции...8 1.6.2. Квадратный трехчлен находится в знаменателе под квадратным корнем…………………………………………………………………………9 1.6.3. Интегралы вида 1.6.4. Подынтегральная функция, содержащая квадратный трехчлен в знаменателе, является неправильной дробью………………………………10 1.6.5. Интегралы вида 1.7.Интегрирование рациональных дробей……………………………….12 1.8. Интегралы от иррациональных функций…………………………….17 1.8.1. Интегралы вида 1.8.2. Интегралы вида 1.8.3. Интегралы вида 1.8.4. Искусственные приемы……………………………………………....20 1.8.5.Тригонометритческие подстановки…………………………………..21 1.9.Интегрирование тригонометрических функций…………………….22 1.9.1. Универсальная тригонометрическая подстановка tg 11.Определенный интеграл……………………………………………...29 2.1.Понятие и основные свойства определенного интеграла………..29 2.2.Оценка определенного интеграла………………….……………….....32 2.3. Теоремы об определенном интеграле………………………………...32 2.4. Вычисление определенного интеграла методом замены переменной……………………………………………………………………33 2.5.Интегрирование определенного интеграла по частям……………..34 2.6.Несобственные интегралы…………………………………………….35 2.6.1. Несобственные интегралы с бесконечными пределами…………35 2.6.2. Несобственные интегралы от разрывных функций……………….36 2.7. Приближенные методы вычисления определенного интеграла……..38 2.7.1. Приближенные методы интегрирования, основанные на геометрической интерпретации определенного интеграла. …………...…38 2.7.2. Приближенное решение интегралов разложением подынтегральной функции в бесконечный степенной ряд……………………………………41 111. Приложения определенного интеграла……………………………42 3.1. Геометрические приложения определенного интеграла……………42 3.1.1.Вычисление площади плоской фигуры в прямоугольной системе координат……………………………………………………………………..42 3.1.2.Вычисление площади плоской фигуры в полярных координатах….44 3.1.3.Вычисление площади плоской фигуры, ограниченной кривой, заданной в параметрическом виде………………………………………….45 3.1.4. Вычисление объёма тела вращения…………………………………46 3.1.5. Вычисление поверхности тела вращения…………………………..47 3.1.6. Вычисление длины дуги кривой……………………………………..47 3.2. Физические приложения определенного интеграла………………..48 3.2.1.Вычисление работы переменной силы……………………………….48 3.2.2.Вычисление массы вещества, концентрация которого меняется с глубиной………………………………………………………………………48 3.3. Экономические приложения определенного интеграла…………….48 3.3.1.Задача на объем произведенной продукции………………………….48 3.3.2.Задача на вычисление среднего времени изготовления одного изделия в период освоения производства…………………………………..49 3.3.3.Задача на вычисление дисконтированной суммы……………………50 3.3.4..Задача на вычисление коэффициента Джини………………………..51 1V. Двойной интеграл……………………………………………………..53 4.1. Общие понятия и методы вычисления ………………………………53 4.2.Приложения двойного интеграла……………………………………...55 4.2.1. Вычисление объема цилиндрического тела………………………….55 4.2.2. Вычисление площади плоской фигуры……………………………....56 4.2.3.Вычисление координат центра тяжести однородной плоской фигуры………………………………………………………………………...57 Приложение. Таблица интегралов..................................................................59 Литература........................................................................................................62
РОСЖЕЛДОР 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а верхняя поверхность которого описывается функцией двух аргументов
, а верхняя поверхность которого описывается функцией двух аргументов  , вычисляется через двойной интеграл согласно его геометрической интерпретации.
, вычисляется через двойной интеграл согласно его геометрической интерпретации. (4.3.)
(4.3.)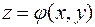 , но её проекция на эту плоскость – область D, то его объем
, но её проекция на эту плоскость – область D, то его объем
 (4.4.)
(4.4.)

 .
.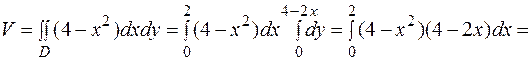



 (4.5.)
(4.5.) и
и 
 -парабола ветвями вверх с вершиной в точке (3,3).
-парабола ветвями вверх с вершиной в точке (3,3). - прямая
- прямая

 Находим координаты точек пересечения
Находим координаты точек пересечения


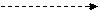 Получили две точки (0,12) и (7,19).
Получили две точки (0,12) и (7,19).
 При «заметании» области D прямой , параллельной оси Оу, точка входа остаётся всё время на параболе , а точка выхода – на прямой. При «заметании» области D прямой , параллельной оси Ох, точка входа переходит с Рис.4.6. левой ветви параболы на прямую, а точка выхода остаётся всё время на правой ветви параболы.
При «заметании» области D прямой , параллельной оси Оу, точка входа остаётся всё время на параболе , а точка выхода – на прямой. При «заметании» области D прямой , параллельной оси Ох, точка входа переходит с Рис.4.6. левой ветви параболы на прямую, а точка выхода остаётся всё время на правой ветви параболы.



 ПРИМЕР 4.4. Вычислить двойным интегралом D
ПРИМЕР 4.4. Вычислить двойным интегралом D
 Рис. 4.7.
Рис. 4.7.

 4.2.3.Координаты центра тяжести однородной плоской фигуры. Если пластина однородна, то есть имеет одинаковую толщину и плотность по всей площади, то координаты её центра тяжестиопределяетсяпо формулам:
4.2.3.Координаты центра тяжести однородной плоской фигуры. Если пластина однородна, то есть имеет одинаковую толщину и плотность по всей площади, то координаты её центра тяжестиопределяетсяпо формулам: =
=  (4.6.)
(4.6.) ПРИМЕР 4.5. Вычислить координаты центра тяжести однородной плоской фигуры, ограниченной линиями
ПРИМЕР 4.5. Вычислить координаты центра тяжести однородной плоской фигуры, ограниченной линиями 




 ,
,  =
=  .
. 2.
2.  3.
3. 
 5.
5.  6.
6.  7.
7. 
 9.
9.  .
. 11.
11.  12.
12.  13.
13. 
 15.
15. 
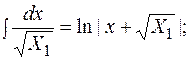 17.
17.  18.
18. 





 24.
24. 
 26.
26. 
 28.
28.  29.
29.  30.
30. 
 .
. 33.
33. 
 35.
35.  36.
36.  37.
37. 
 39.
39.  40.
40.  .
. 42.
42. 
 44
44 
 46.
46. 
 48.
48. 
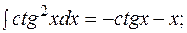 50.
50. 
 52.
52. 

 55.
55. 

 58.
58.  59.
59.  60.
60. 
 62.
62. 

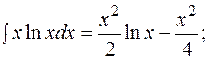 64.
64. 

 …………………………………...10
…………………………………...10 ……………… ………………11
……………… ………………11 …………………………….17
…………………………….17 ………….17
………….17 …………………………..18
…………………………..18 ……….22 1.9.2.Частные случаи………………………………………………………...23
……….22 1.9.2.Частные случаи………………………………………………………...23