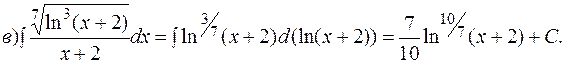|
|
Интегрирование методом подведения под знак дифференциала.Е.П. Рычков ВЫСШАЯ МАТЕМАТИКА Интегральное исчисление Учебное пособие.
Кропоткин ББК22.11я .73 Р93 Рычков Е.П., к.в.н. доцент. Высшая математика.Интегральное исчисление.Учебное пособие.
Рост.н/Д: Рост.гос.ун-т путей сообщения, 2010.- с. 64.
Учебное пособие рассчитано, прежде всего, на студентов экономических специальностей ВУЗов. Оно раскрывает один из сложнейших разделов высшей математики, "Интегральное исчисление", в объеме необходимом и достаточном для студентов экономических специальностей. Рассматриваются основные понятия, неопределенные, определенные, кратные интегралы, методы нахождения первообразных функций, точные и приближенные методы вычисления; приводится множество примеров вычисления интегралов, решения задач на применение определенного и двойного интеграла; приведено более 150 формул, используемых в разделе "Интегральное исчисление". Пособие содержит таблицы и 38 графиков Кроме теоретического материала в учебном пособии приведены примеры решения различных задач, в том числе задач экономической теории. Пособие содержит 300 базовых, ключевых примеров с подробными решениями. Рецензенты: к.т.н. проф. РГУ ПС Г.Г.Гарбуз к.т.н. проф. МГОУВ.П.Шевцов
типография", 2010 – 64с.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Определение и основные свойства неопределенного интеграла. Функция F(x) называется первообразной для функции Любая непрерывная функция Совокупность первообразных
где
Основные свойства неопределенного интеграла. 1.Производная от неопределенного интеграла равна подынтегральной функции:
2.Дифференциал от неопределенного интеграла равен подынтегральному выражению:
3.Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
4.Постоянный множитель можно выносить за знак интеграла:
7. Если а) б) в) Для проверки правильности вычисления неопределенного интеграла необходимо продифференцировать полученный результат.
Таблица основных интегралов.
Часто к основным относят также интегралы:
Методы интегрирования зависят от вида подынтегральной функции. Различают: · непосредственное интегрирование, · интегрирование заменой переменной (метод подстановки), · интегрирование подведением части подынтегральной функции под знак дифференциала, · интегрирование по частям, · интегрирование функций, содержащих квадратный трёхчлен, · интегрирование рациональных дробей, · интегралы от иррациональных функций, · интегрирование тригонометрических функций. Непосредственное интегрирование. Интегрирование, основанное на применении таблицы интегралов, основных свойств неопределенного интеграла, а также на простейших тождественных преобразованиях подынтегральной функции, принято называть непосредственным интегрированием. ПРИМЕР 1.1. Найти интегралы. а) в) г)
е) ж) з) и) к) Интегрирование заменой переменной (метод подстановки). Метод применяется, если интеграл не является табличным, но заменой переменной можно свести данный интеграл к табличному (одному или нескольким). После вычисления интеграла необходимо вернуться к исходной переменной. То есть, метод использует свойство инвариантности. ПРИМЕР 1.2. Найти интегралы методом подстановки.
Интегрирование методом подведения под знак дифференциала. Подведение функции или ее части под знак дифференциала (преобразование функции под знаком дифференциала) позволяет получить табличный интеграл (с учетом свойства инвариантности). ПРИМЕР 1.3. Найти интегралы методом подведения под знак дифференциала.
Здесь под знак дифференциала подвели выражение

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , если выполняется
, если выполняется 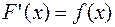 на том же интервале.
на том же интервале. С, где С - произвольная постоянная, называется неопределенным интеграломфункции
С, где С - произвольная постоянная, называется неопределенным интеграломфункции 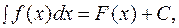 (1.1.)
(1.1.)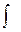 - знак интеграла,
- знак интеграла,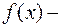 подынтегральная функция,
подынтегральная функция,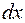 - подынтегральное выражение.
- подынтегральное выражение.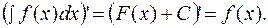 (1.2.)
(1.2.)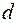 (
( 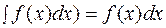 . (1.3.)
. (1.3.)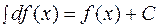 . (1.4.)
. (1.4.)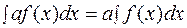 , где
, где 
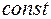 . (1.5.) 5. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов:
. (1.5.) 5. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов: . (1.6.) 6.Формулы интегрирования обладают свойством инвариантности. То есть, формула не меняется, если в ней переменную заменить дифферен- цируемой функцией от неё, а дифференциал аргумента заменить дифферен- циалом этой функции.
. (1.6.) 6.Формулы интегрирования обладают свойством инвариантности. То есть, формула не меняется, если в ней переменную заменить дифферен- цируемой функцией от неё, а дифференциал аргумента заменить дифферен- циалом этой функции.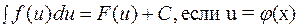 .
.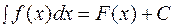 , то
, то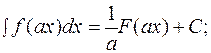 (1.7.1.)
(1.7.1.)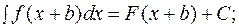 (1.7.2.)
(1.7.2.)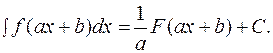 (1.7.)
(1.7.)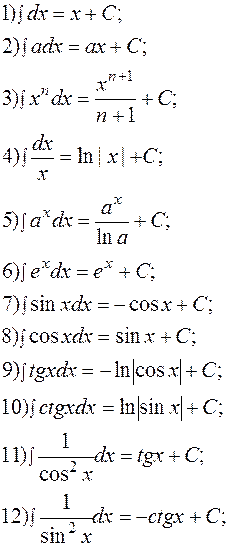 .
. 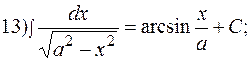

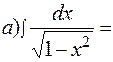

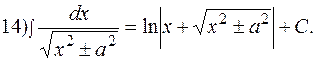

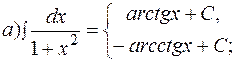
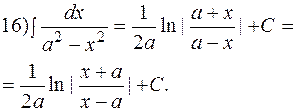
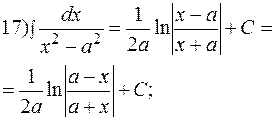
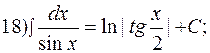

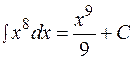 . б)
. б) 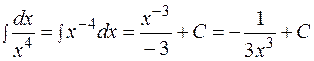 .
.
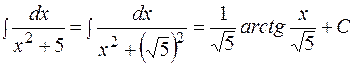 .
.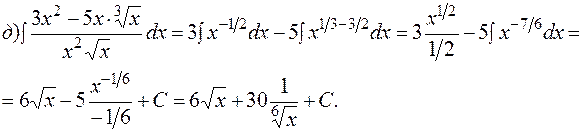 .
.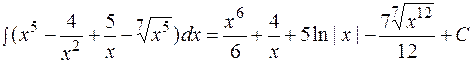 .
. .
. .
. Согласно (1.7)
Согласно (1.7)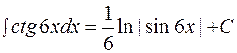 .
.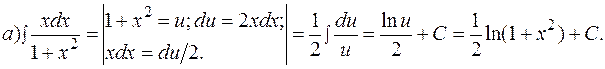
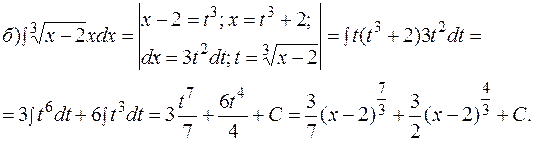 .
. 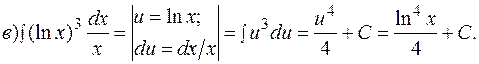
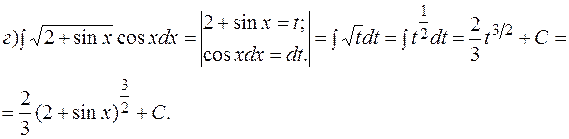
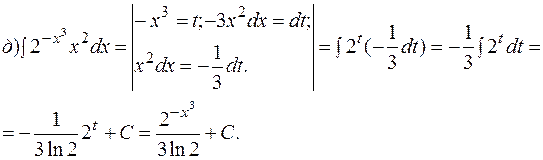
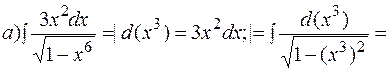
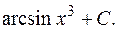
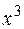 .
.