
|
|
Алгоритм разложения правильной дроби на простейшие.1) Знаменатель дроби представить в виде произведения:
где
2) Каждому множителю в знаменателе поставить в соответствие простейшую дробь: множителю множителю множителю множителю 3) записать правильную исходную дробь суммой простейших дробей, найденных в п.2. 4) найти коэффициенты А,В,С,… методом неопределенных коэффициентоводним из способов.
Способ "сравнения коэффициентов" · сложить простейшие дроби, приведя их к общему знаменателю; · отбросить знаменатель, а в числителе привести подобные члены по степеням · сравнивая коэффициенты при степенях · решить полученную систему любым способом. Способ "подборачастных решений": · расставить дополнительные множители для приведения дробей к общему знаменателю; · составить тождество, в левой части которого – сумма произведений числителей простейших дробей на дополнительные множители, а в правой части – числитель исходной дроби; · придавая переменной · решить полученную систему. ПРИМЕР 1.11. Найти интеграл Подынтегральная функция – правильная рациональная дробь. Представляем её в виде суммы простейших дробей.
Находим коэффициенты А, В, С. 1. Способ "сравнения коэффициентов".
Решаем систему матричным методом Гаусса.
2. Способ "подбора частных решений".
При При При Подставляем значения А, В, С и находим интеграл.
ПРИМЕР 1.12. Разложить дробь РЕШЕНИЕ. Дробь правильная рациональная, поэтому
Способом подбора частных решений находим коэффициенты
При
При При
Делим 1-е уравнение на 2, и из него получаем: Подставляем коэффициенты и получаем искомое разложение исходной правильной дроби на простейшие.
Интегралы от иррациональных функций. Не от всякой иррациональной функции интеграл выражается через элементарные функции, то есть интегрируется. Рассмотрим некоторые интегрирующиеся функции.
1.8.1. Интегралы вида где
Применяя подстановку где указанный интеграл преобразуется в интеграл от рациональной функции. ПРИМЕР 1.13. Найти интеграл РЕШЕНИЕ.
следовательно, заменяем переменную = = 1.8.2. Интегралы вида где указанный интеграл преобразуют в интеграл от рациональной функции. ПРИМЕР 1.14. Найти интеграл а) РЕШЕНИЕ. Общий знаменатель дробей
= б) РЕШЕНИЕ. Делаем подстановку:
1.8.3. Интегралы вида Эйлера. Я подстановка Эйлера. Если Положим знак плюс и возведем в квадрат обе части равенства
откуда Тогда ПРИМЕР 1.15. Найти интеграл РЕШЕНИЕ. Принимаем:
Я подстановка Эйлера. Пусть тогда применяется подстановка Возводим в квадрат и выражаем квадратный трехчлен через его корни
Данная подстановка применима как при ПРИМЕР 1.16. Найти интеграл
РЕШЕНИЕ. Корни трехчлена Полагаем Возведём в квадрат обе части и сократим на (
=
Искусственные приемы. ПРИМЕР 1.17. Найти интегралы а) =
Последнее слагаемое - есть исходный интеграл поэтому, перенеся его влево от знака равенства и разделив на 2, получаем:
Интегрирование иррациональных функций, содержащих квадратные трехчлены, рассмотрены в п.1.5.
1.8.5.Тригонометритческие подстановки. Если подынтегральная функция содержит корни вида: Для интегралов вида подстановка вида подстановка вида подстановка
ПРИМЕР 1.18. Найти интегралы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 корень многочлена. Если корни повторяются k раз, то записывают
корень многочлена. Если корни повторяются k раз, то записывают  если корни комплексные
если корни комплексные  то
то
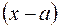 - простейшую дробь 1 типа
- простейшую дробь 1 типа  ,
, сумму
сумму 
 - дробь III типа
- дробь III типа 
 - сумму
- сумму 
 ;
;









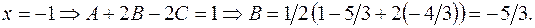


 на простейшие.
на простейшие.
 .
.


 При
При 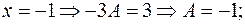


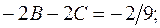


 Вычтя 2-е уравнение из 1-го, получаем:
Вычтя 2-е уравнение из 1-го, получаем: 

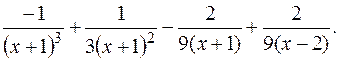
 , (1.16.)
, (1.16.) означает, что над величинами
означает, что над величинами  производятся только рациональные операции;
производятся только рациональные операции; - целые числа.
- целые числа. (1.17.)
(1.17.) - наименьший общий знаменатель дробей
- наименьший общий знаменатель дробей 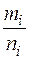 ,
,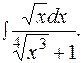
 |общий знаменатель дробей
|общий знаменатель дробей  и
и 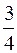 является 4,
является 4, =
=

 . (1.18.) Подстановкой
. (1.18.) Подстановкой  (1.19.)
(1.19.)
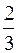 является 6, следовательно, замена переменной:
является 6, следовательно, замена переменной: 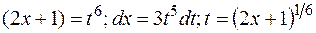 .
.

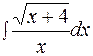 .
. .
.
 (1.20.) приводятся к интегралам от рациональных функций подстановками
(1.20.) приводятся к интегралам от рациональных функций подстановками то полагаем
то полагаем 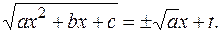 (1.21.)
(1.21.)
 рациональная функция от
рациональная функция от 

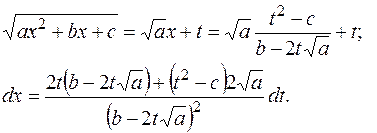
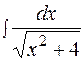 .
. тогда
тогда  ;
;

 и
и 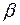 - действительные корни трехчлена
- действительные корни трехчлена 
 (1.22.)
(1.22.) ;
; 
 рациональное выражение.
рациональное выражение.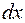 и
и  также рационально зависят от
также рационально зависят от  так и при
так и при  , но многочлен
, но многочлен  должен иметь два действительных корня.
должен иметь два действительных корня.
 = - 4;
= - 4;  = 1 – действительные числа, поэтому
= 1 – действительные числа, поэтому 
 .
.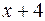 ).Получаем:
).Получаем: 
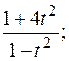



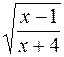 ;
; 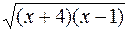 =
= 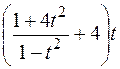 =
=  . Тогда:
. Тогда: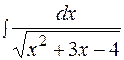 =
=  +C =
+C =
 +C =
+C =  .
.
 б)
б) 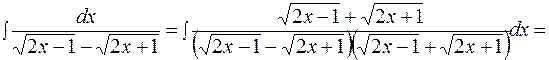

 в)
в) 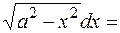 |
|  |=
|= 


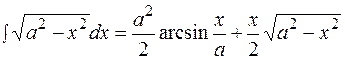
 то применяются тригонометрические подстановки.
то применяются тригонометрические подстановки. -
-
 (1.23.)
(1.23.) -
- или
или  (1.24.)
(1.24.) -
- или
или  (1.25.)
(1.25.)




