
|
|
Теоремы об определенном интеграле.1) Теорема осреднем. Если
переменному пределу равна подынтегральной функции от верхнего х
Интеграл с переменным верхним пределом Рис. 2.4. Выражает площадь криволинейной трапеции с подвижной правой боковой стороной (рис. 2.4.) Используя 1-е свойство неопределенного интеграла запишем
Данная теорема применяется для доказательства теоремы Ньютона - Лейбница. 3) Теорема Ньютона - Лейбница. Если F(
Формула Ньютона - Лейбница используется для вычисления определенных интегралов. ПРИМЕР 2.2. Вычислить определенные интегралы.
Вычисление определенного интеграла методом замены переменной. Заметим, что значение определенного интеграла не зависит от обозначения переменной интегрирования, а зависит только от подынтегральной функции и пределов интегрирования. Поэтому при замене переменной нет необходимости после нахождения первообразной возвращаться к исходной переменной, но при замене переменной пределы интегрирования необходимо заменять новыми, соответствующими новой переменной. ПРИМЕР 2.3. Вычислить интегралы методом замены переменной.
Можно пределы подставить и так:
Интегрирование определенного интеграла по частям. При интегрировании определенного интеграла по частям применяется формула:
ПРИМЕР 2.4. Вычислить интегралы методом интегрирования по частям.
=
= Несобственные интегралы. Если подынтегральная функция f(x) рвется на [a,b] или пределы интегрирования являются бесконечными Различают: - несобственные интегралы с бесконечными пределами, - несобственные интегралы от разрывных функций. 2.6.1.Несобственные интегралы с бесконечными пределами.
Геометрический смысл сходящегося 0а интегралас бесконечными пределами – Рис.2.5. площадь неограниченной криволинейной трапеции (рис.2.5.), заключенной между кривой Таким образом, Аналогично
ПРИМЕР 2.5. Вычислить несобственный интеграл или установить его расходимость.
Возможна и другая форма записи:
2.6.2.Несобственные интегралы от разрывных функций.
(рис.2.6.). Поэтому применяется запись:
То есть интеграл от разрывной функции 0 равен сумме интегралов согласно 5-му Рис.2.6. свойству определенного интеграла.
асимптоты, рис.2.7.) :
Для правостороннего разрыва (справа от 0
Рис.2.8.
сторон от асимптоты, рис.2.9.):
В последнем случае интеграл сходится, если оба предела существуют. ПРИМЕР 2.6. Вычислить несобственный Рис.2.9. интеграл от разрывной функции или установить его расходимость.
Исследуем на сходимость каждый интеграл.
Интеграл Заметим, что если точек разрыва не заметить, к интегрированию подойти формально, то получаем:
что не верно.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 непрерывна на [a,b], то на этом отрезке существует, по крайней мере, одна точка
непрерывна на [a,b], то на этом отрезке существует, по крайней мере, одна точка  , такая, что
, такая, что  . Геометрический смысл теоремы – площадь прямоугольника с высотой
. Геометрический смысл теоремы – площадь прямоугольника с высотой 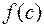 и основанием
и основанием  равна площади криволинейной трапеции, вычисляемой интегралом
равна площади криволинейной трапеции, вычисляемой интегралом  .
. 2)Теорема о производной от определенного интеграла по переменному верхнему пределу доказывает, что, если
2)Теорема о производной от определенного интеграла по переменному верхнему пределу доказывает, что, если 



 то есть производная
то есть производная  от определенного интеграла по верхнему
от определенного интеграла по верхнему предела. 0
предела. 0 


 Ф(х) .
Ф(х) . (
( 
 (2.3.)
(2.3.) .
.






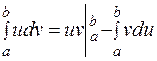 , где u = u (x),v = v(x).
, где u = u (x),v = v(x).






 =
=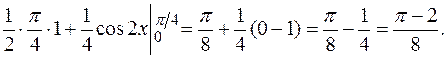

 то интеграл называется несобственным.
то интеграл называется несобственным.


 является сходящимся, если от него существует предел
является сходящимся, если от него существует предел 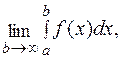 у
у  интеграл расходится и смысла не имеет. х
интеграл расходится и смысла не имеет. х ), прямой
), прямой  и асимптотой
и асимптотой 


 .
.


 интеграл расходится.
интеграл расходится.

 Если функция терпит разрыв 1-го рода,
Если функция терпит разрыв 1-го рода,


 то в точке разрыва имеется конечный скачек
то в точке разрыва имеется конечный скачек 






 Если функция терпит разрыв 2-го рода, то в точке разрыва скачек бесконечный и применяются записи, зависящие от места разрыва функции (на краях отрезка
Если функция терпит разрыв 2-го рода, то в точке разрыва скачек бесконечный и применяются записи, зависящие от места разрыва функции (на краях отрезка  или внутри него).
или внутри него).  Для левостороннего разрыва (слева от
Для левостороннего разрыва (слева от 

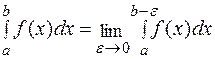 .
. 


 асимптоты, рис.2.8.):
асимптоты, рис.2.8.): 


 0
0 


 Для двустороннего разрыва (с обеих
Для двустороннего разрыва (с обеих 



 0 а с b x
0 а с b x При
При  знаменатель подынтегральной функции обращается в 0, терпит правосторонний разрыв 2-го рода, поэтому:
знаменатель подынтегральной функции обращается в 0, терпит правосторонний разрыв 2-го рода, поэтому:
 Функция терпит разрыв 2-го рода в точках
Функция терпит разрыв 2-го рода в точках  Вторая точка выходит за пределы интервала интегрирования. Таким образом:
Вторая точка выходит за пределы интервала интегрирования. Таким образом:

 расходится, следовательно, исходный интеграл также расходится.
расходится, следовательно, исходный интеграл также расходится.
 ,
, , называемый интегралом Эйлера – Пуассона.
, называемый интегралом Эйлера – Пуассона. Доказано, что
Доказано, что  . Площадь фигуры под бесконечной кривой Гаусса
. Площадь фигуры под бесконечной кривой Гаусса  .
.  . (Рис.2.10.) Рис.2.10.
. (Рис.2.10.) Рис.2.10.