
|
|
Экстремумы функций двух переменных.
С помощью частных производных можно отыскать точки экстремумов функции и определить их характер. Так необходимым признаком того, что точка
Точки, в которых эти условия выполняются, по – прежнему будем называть критическими. Достаточным признаком того, что критическая точка действительно экстремальна, является выполнение в этой точке неравенства
При этом, если
Если Пример: Найти экстремуму функции
Решение
Векторная функция скалярного аргумента
Назвем вектор - функцией скалярного аргумента правило по которому каждому значению числовой (скалярной) переменной t ставится в соответствие единственный и четко определенный радиус вектор
это так: 
Ясно, что для того, чтобы задать вектор
Естественно вектор
Называют производнойвектор – функции скалярного аргумента.
Из свойств пределов и операций с координатами вектора следует, что
Кривая (траектория), которую описывает конец М радиус - вектор  , называется годографом вектор - функции. Тогда, если трактовать t как время (а годограф - как траекторию движения), то вектор , называется годографом вектор - функции. Тогда, если трактовать t как время (а годограф - как траекторию движения), то вектор  , очевидно, выражает вектор скорости движения «материализовавшейся» точки М вдоль соответствующего годографа. , очевидно, выражает вектор скорости движения «материализовавшейся» точки М вдоль соответствующего годографа.
Геометрически, и это следует из определения вектор
Рассмотрим «плоскую» вектор - функцию Тогда уравнения которое определяют своеобразную зависимость «у от х» через «общий» аргумент t называют параметрическими уравнениями плоской кривой или уравнениями функции «у от х» «заданной параметрически». Естественно, и в этом случае можно говорить о производной «от у по х», то есть о
. (*)
Последнее уравнение здесь (в правой части - выражение «от t») и определяет параметрическую зависимость «у' от х». Эти же последние уравнения определяют и «методику» нахождения «старших» производных (второй, третьей и т.д.) от функции заданной параметрически. Нужно рассматривать каждую «предыдущую» производную, как «новую», параметрически заданную функцию, и записывать для нее соответствующие уравнения (*) как для «первой» производной. Пример:
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 1
1. Решить систему тремя способами: а) с помощью обратной матрицы, б) по правило Крамера, в) с помощью процедуры Гаусса.
1)
3)
5)
7)
9)
11)
13)
15)
17)
19)
21)
23)
25)
27)
3. Для пирамиды А,В,С,D, координаты вершин которой заданы в таблице 2, найти: координаты и длины векторов ребер Таблица 2
4. Построить кривые приведя их уравнения к каноническому виду
1) 3)
5)
7)
9)
11)
13)
15)
17)
19)
21)
23)
25)
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ № 2
1. Найти указанные пределы (в п.2 можно использовать эквивалентность бесконечно малых переменных величин).
1)
4)
7)
10)
13)
16)
19)
22)
25)
2. Найти у' (х) для функций заданных (а) - явно и (в) - неявно, используя во втором случае частные производные от соответствующей функции двух переменных.
1) а)
2) a)
3) a)
4) a)
5) a)
6) a)
7) a)
8) a)
9) a)
10) a)
11) a)
12) a)
13) a)
14) a)
15) a)
16) a)
17) a)
18) a)
19) a)
20) a)
21) a)
22) a)
23) a)
24) a)
25) a)
4. Для функции а) полный дифференциал, б) градиент в точке М0 (х0,у0):
4.1. 4.2. 4.3 4.4. 4.5. 4.6. 4.7. 4.8. 4.9. 4.10. 4.11. 4.12. 4.13. 4.14. 4.15. 4.16. 4.17. 4.18. 4.19. 4.20. 4.21. 4.22. 4.23. 4.24. 4.25.
Номер варианта определяется следующей таблицей.
ЛИТЕРАТУРА 1. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. Т. 1,2.-М.: Высшая математика. 1978. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 является точкой минимума (максимума) то есть точкой экстремума дифференцируемой функции, является выполнение в этой точке условий:
является точкой минимума (максимума) то есть точкой экстремума дифференцируемой функции, является выполнение в этой точке условий: .
.

 , то
, то  - точка максимума, а если
- точка максимума, а если  , то
, то  , то критическая точка не экстремальна (она называется в этом случае седловой точкой). Если же
, то критическая точка не экстремальна (она называется в этом случае седловой точкой). Если же  , то вопрос о характера критической точки открыт (требуются дополнительные исследования).
, то вопрос о характера критической точки открыт (требуются дополнительные исследования). .
. , отсюда М0 (-2,3) - критическая точка
, отсюда М0 (-2,3) - критическая точка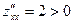 ;
;  ;
;  М0 (-2,3) - точка минимума.
М0 (-2,3) - точка минимума. (см. рис.), записывая
(см. рис.), записывая 
 , то есть
, то есть называют приращением вектор - функции
называют приращением вектор - функции 

 .
. ).
).
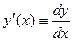 . Можно показать, что она также является функцией заданной параметрически и определяется уравнениями
. Можно показать, что она также является функцией заданной параметрически и определяется уравнениями
 ;
;  ;
;  ;
;  ; .....
; ..... 2)
2) 
 4)
4) 
 6)
6) 
 8)
8) 
 10)
10) 
 12)
12) 
 14)
14) 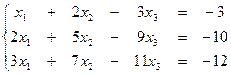
 16)
16) 
 18)
18) 
 20)
20) 
 22)
22) 
 24)
24) 
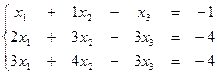 26)
26) 

 ,
,  ,
,  угол ВАС, площадь гран (ВАС) и объём пирамиды; уравнения ребра (АD), грани (ВАС), а также высоту и длину высоты (DН).
угол ВАС, площадь гран (ВАС) и объём пирамиды; уравнения ребра (АD), грани (ВАС), а также высоту и длину высоты (DН). 2)
2) 
 4)
4) 
 6)
6) 
 8)
8) 
 10)
10) 
 12)
12) 
 14)
14) 
 16)
16) 
 18)
18) 
 20)
20) 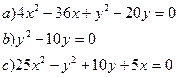 22)
22) 
 24)
24) 

 2)
2)  3)
3) 
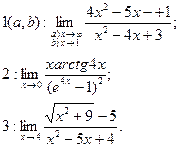 5)
5)  6)
6) 
 8)
8)  9)
9) 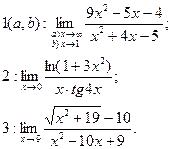
 11)
11)  12)
12) 
 14)
14)  15)
15) 
 17)
17)  18)
18) 
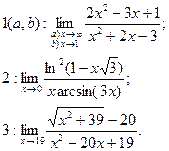 20)
20)  21)
21) 
 23)
23)  24)
24) 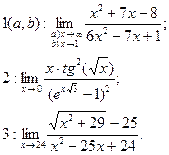

 ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  b)
b)  .
. ; b)
; b)  .
. ; b)
; b)  ; b)
; b)  .
. ; b)
; b)  .
. ; b)
; b)  .
. найти
найти , М0 (1;1)
, М0 (1;1) , М0 (1;2)
, М0 (1;2) , М0 (2;1)
, М0 (2;1) , М0 (4;1)
, М0 (4;1) , М0 (0;3)
, М0 (0;3) , М0 (2;0)
, М0 (2;0) , М0 (1;4)
, М0 (1;4) , М0 (0;4)
, М0 (0;4) , М0 (3;2)
, М0 (3;2) , М0 (2;3)
, М0 (2;3) , М0 (5;0)
, М0 (5;0) , М0 (1;5)
, М0 (1;5) , М0 (4;2)
, М0 (4;2) , М0 (2;4)
, М0 (2;4) , М0 (4;4)
, М0 (4;4) , М0 (5;3)
, М0 (5;3) , М0 (3;3)
, М0 (3;3) , М0 (3;-1)
, М0 (3;-1) , М0 (-1;1)
, М0 (-1;1) , М0 (-2;1)
, М0 (-2;1) , М0 (2;2)
, М0 (2;2) , М0 (0;5)
, М0 (0;5) , М0 (1;0,5)
, М0 (1;0,5) , М0 (-1;2)
, М0 (-1;2) , М0 (-2;-1)
, М0 (-2;-1)