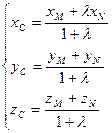|
|
Основные определение и обозначенияВОЛЖСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВОДНОГО ТРАНСПОРТА
Кафедра математики
В.Н. Белых, Я.Н. Сенниковский
ОСНОВНЫЕ ПОНЯТИЯ ИЗ ЛИНЕЙНОЙ АЛГЕБРЫ И ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.
Методические указания для студентов заочного обучения технических специальностей
Н. Новгород
Настоящее пособие адресовано студентам всех специальностей заочного обучения. Оно призвано помочь им в освоении необходимого минимума теоретического материала и привить определенные навыки для решения задач контрольной работы № 1 и № 2. Подготовить к сдаче зачета и экзамена по темам: «Решение систем линейных уравнений», «Основы векторной алгебры и аналитической геометрии» и «основные понятия дифференциального исчисления». Изложены основные понятия приведены примеры решения задач и даны задания для выполнения контрольной работы № 1 и № 2.
Азбука…собрание в порядок…какой либо грамоты,…учебник грамоты, букварь: начальные основания какой- либо науки… Азбука наука, а ребятам бука (мука)… В. Даль «Толковый словарь…»
МАТРИЧНАЯ АЗБУКА
Основные определения и обозначения
Матрицей размерами "m на n" или коротко, (m x n) - матрицей называется таблица из m строк и n столбцов, элементами которой могут быть числа, буквы, вектора, матрицы, а также любые математические выражения, составленные из них. Изображаютматрицу как обведенную круглыми скобками таблицу
а обозначаютзаглавными буквами латинского или русского алфавита - А, В, С, D и т.д. Элементы матриц, как видно из ее изображения, обозначают соответствующими малыми буквами аij, bij¸ … где i указывает номер строки, а j - номер столбца, в которых этот элемент находится.
Действия с матрицами
1. Матрица размерами "n на m" называется транспонированной по отношению к данной (m x n) – матрице если каждая е строка является соответствующим столбцом данной. Обозначают такие «взаимно транспонированные» матрицы одной и той же буквой, добавляя к одной из них верхний индекс «т», например: А и АТ, ВТ и В и т.д. Примеры: В =
II. Суммой двух матриц одинаковых размерностей, например А и В, называется новая матрица С тех же размеров элементы которой сij = аij + bij
III. Произведением матрицы А на число λ называется матрица В элементы которой bij = λ aij Действия II. и III. Называют линейными действиями с матрицами, а выражения типа "αА + βВ" - линейными комбинациями матриц.
Пример 2 ·
IY. Произведением ( 1 х n ) - матрицы строки на( n х 1 ) - матрицустолбец называется (1х1) - матрица единственный элемент которой с 1 1 = Пример (1 -1 3) · Y. Произведением (m х n) - матрицы А на (n х p) - матрицу В называется (m х р) - матрица С Элементами которой является элементы (1 х 1) – матриц, образующихся при перемножении i – ой стройки А на j – ый столбец В. Таким образом сij =
Примеры 1)
2)
3)
Особую роль при перемножении играет так называемая единичная (
Как и числовая единицы, эта матрица при умножении (если это допустимо) на любую другую не изменяет последнюю. Например А · Е =
Определители матриц.
Понятие определить или (синоним) детерминант матрицы вводится для любой квадратной и только квадратной матрицы. Изображаютопределитель любой такой матрицы А = «сложным» символом
а обозначают чаще всего одним из символов ∆ (а), det (A), или просто ∆. Договорились, что определителем квадратной матрицы называется величина, формируемая из её элементов с помощью следующих понятий и соглашений: ¨ Определителем матрицы первого порядка называют её единственный элемент; ¨ Минором (ЛЮБОЙ!!!) матрицы называют определитель всякой квадратной матрицы встроенной в данную. Другими словами минором к- го порядка некоторой матрицы состоящей из элементов данной матрицы, которые находились на пересечении любых её "k" строк и "k" столбцов. ¨ Дополнительным минором к элементу аij квадратной матрицы А называют минор – определитель М*ij матрицы, полученной из данной вычеркиваниемi – ой строки и j – го столбца. ¨ Алгебраическим дополнением к элементу аij квадратной матрицы А называют величину А*ij = (-1)i+j · М*ij
Процесс вычисления определителя по такой формуле часто называют разложением определителя по (первой) строке. Из вышеизложенного сразу следует что: А. Для n = 2, то есть для матрицы А = А*12 = (-1)3 · М*12 = - а 21, а значит det (А) = а11 · А11 + а12 · А12, то есть
Б. Для n = 3, то есть для матрицы А = М*13 =
Примеры:
Свойства определителей
1. Для любых 1 ≤ i ≤ n
Иначе говоря, определитель всякой матрицы может быть вычислен «разложением по любой строке. Пример:
2. Из этого свойства и свойства 1., в частности, следует, что определитель может быть вычислен для любого 1 ≤ j ≤ n по формуле
то есть «разложением» по любому столбцу. Пример. Раскладывая определитель из первого примера по первому, второму и третьему столбцу последовательно получаем:
3. Если k – тый (1 ≤ k ≤ n) столбец (строка) матрицы представлен в виде суммы неких двух столбцов (строк), то её определитель может быть получен как сумма определителей матриц у которых k – тым столбцом является соответствующий столбец (строка) - слагаемое. Пример: Все для того же определителя ∆ имеем -2 = ∆ = 4. При умножениистолбца (строки) матрицы на число λ её определитель умножается на то же самое число. Пример: Умножив в «нашем» ∆ на вторую строку на 5 и раскладывая по этой строке «новый» определитель получаем
5. При перестановке двух любых строк (столбцов) матрицы её определитель меняет знак.
Пример. Переставив «в ∆» первую и третью строку получаем
6. Равен нулю определитель любой матрицы имеющей две одинаковые строки (столбца). Пример: Из этого свойства, в частности, следует что равна нулю сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) то есть
7. Определитель матрицы не меняется, если к любой её строке (столбцу) прибавить произвольную комбинацию остальных строк Пример: прибавив ко второй и третьей строкам определителя ∆ его же первую, получаем:
Обратная матрица
Квадратные матрицы А и В называются взаимно обратными если
то есть если их произведение перестановочно и равно соответствующей единичной матрице. Матрицу, обратную к данной принято обозначать той же буквой, помечая её верхним индексом «-1». Например А и А-1, В и В-1 и т.д. Квадратная матрица называется невырожденной, если ёё определитель отличен от нуля.
Можно показать, что обратная матрица А-1 получается из исходной невырожденной матрицы А следующим образом: 1. Вычисляются ∆ = det (А) ≠ 0, и все А*ij. 2. Составляется так называемая присоединенная матрица 3. 4. Матрица
Примеры: 1. В = ∆ = ВТ = Проверка В-1 · В =
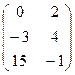
2. С = СТ =
Проверка:
С-1 · С =
Ранг матрицы.
Введенное выше понятие минора является более общим, нежели детерминант понятием имеющим место, как для квадратных, так и для произвольных матриц. К таковым же относится и понятие базисного минора и, наконец, ранга матрицы. Как уже говорилось минором k – го порядка (не путать с «дополнительным минором2!) называется определитель квадратной матрицы k – го порядка, «встроенной» в данную, т.е. матрицы состоящей из элементов которые расположены на пересечении выделенных k строк и k столбцов. Их иногда обозначают символами вида
где is (js) - номера выделенных строк (столбцов) данной матрицы. Например
А =
Очевидно, что часть таких миноров отлична от нуля, а часть возможно и равна нулю. Так вот Базисным минором называется любой такой минор, если он отличен от нуля, но все миноры высшего порядка равны нулю или не существуют. Наконец рангом матрицы, обозначаемым как Rang (А) называется порядок (размерность) такого базисного минора. Так, в последнем примере, Rang (А) = 2, так как имеется отличный от нуля минор второго порядка, но все четыре минора третьего порядка равны (проверь) нулю, а высшего чем три – не существует. Заметим здесь же, что ранг невырожденной квадратной матрицы равен ее порядку, так как ее базисный минор это её собственный определитель. Ранг же матрицы столбца (строки) равен 1. Отметим здесь также, что определитель так называемой треугольной матрицы k – го порядка, т.е. матрицы Тk у которой tij=0, если i>j, но все tss≠0, равен (проверь) произведению диагональных элементов, а, следовательно, отличен от нуля и значит ранг её равен k. Т(k) = Для нахождения ранга матрицы можно применить так называемые элементарные преобразования матриц не меняющие её ранга: это - перестановка строк (столбцов); умножение строки (столбца) на отличное от 0 число; прибавление к одной строке «линейной комбинации» остальных строк, т.е. последовательное или одновременное добавление к ней всяких других строк данной матрицы, предварительно умноженных на какие – либо числа. Матрицы, получаемые одна за другой с помощью таких преобразований, называют эквивалентными матрицами. Любая (m x n) матрица может быть преобразована с помощью цепочки таких элементарных преобразований в так называемую трапециевидную матрицу изображённую ниже. Это матрица Тr у которой в левом верхнем углу встроена треугольная матрица k – го порядка, где k≤min {m¸n}, а все строк5и лежащие под k – ой строкой (если они существуют) целиком забиты нулями. Очевидно, что минор det (Тk) базисный и ранг Тr равен k. Процедура приведения к такому виду состоит из нескольких шагов и заключается в следующем. Доля того чтобы на s – ом шаге (s = 1,2,...k) привести s-ый столбец к виду (*) то есть сделать все ts+r s=0¸r= 1,2,...m-s; надо при аss≠0 (а «это» можно «организовать» перестановкой строк или столбцов) вычесть из s+r – ой строки s – ую строку, умноженную на λ = аr+s s/аs s. Описанная процедура нахождения ранга называется процедурой Гаусса.
Пример
Rang A1 = Rang Tr1 = 2
Решение систем
Все приведенные в матричной азбуке понятия применимы прежде всего для решения систем линейных алгебраических уравнений («линейных систем») то есть систем вида
Решением такой системы m – линейных уравнений с n – неизвестными называется упорядоченный набор (х01, х02, ...., х0n) значений всех его неизвестных, удовлетворяющий всем уравнениям системы. Матрицы А = Называются соответственно главная - А, матрица столбец неизвестных - Х, и матрица - столбец свободных членов - В. С помощью этих матриц система (*) может быть переписана в так называемой матричной форме
То есть как Остановимся на трех методах решения таких систем. Это - для m=n – так называемые «метод обратной матрицы» и «метод Крамера», а, - для любых m и n, - «метод Гаусса».
I. Метод обратной матрицы.
Пусть данная линейная система имеет главную невырожденную квадратную матрицу А. перепишем систему в виде линейного матричного уравнения А·Х=В и, найдя А-1 умножим, это матричное уравнение слева на матрицу А-1, то есть придем к уравнению А-1· А · Х = А-1 · В. Учтя, что А-1· А = Е и Е· Х = Х, получаем формулу для решения данной системы в матричном виде
(**) Пример
Ответ: (2, 1, -1).
II. Правило Крамера.
Было вместе с определителями пере изобретено женевским математиком Крамером в семидесятых годах XVIII века, хотя к идее детерминантов и применению их к решению систем почти за семьдесят лет до этого пришел лейбниц. Впрочем, тогда же о них благополучно забыли. Примечательно и то, что определителем изучались и применялись как Лейбницем, так и Крамером без какого – либо отношения к матрицам, которые были придуманы ещё почти сто лет - в конце XIX века. И «только теперь» мы можем открыть для себя «страшную тайну» - праило Крамера это ни что иное, как метод обратной матрицы расписанный покоординатно. Действительно, вспомнив, что каждая строка матрицы А-1 это столбец алгебраических дополнений А*ki, 1 ≤ k ≤ n, поделённый на определитель ∆ главной матрицы выпишем i – ый элемент матрицы А-1 · В, то есть i – ую компоненту решения полученного с помощью формулы (**):
Сравнивая теперь числитель этой формулы с разложением определителя по i – му столбцу (см. свойство (2) определителей) убеждаемся, что и его (числитель) можно восстановить в некий определитель ∆xi матрицы, которая отличается от главной лишь тем, что её i – ый столбец это столбец свободных членов системы. Так вот, переписанная в виде
(***)
она и являет собой правило Крамера.
Пример:
∆ =
Ответ: (2, 1 -1).
III. Метод Гаусса
Если m и n не связаны условием равенства или ∆ = 0, то есть линейная система формально не может быть решена с помощью описанных выше методов, то для её решения можно применить описанную выше процедуру Гаусса. Для этого введем в рассмотрение так называемую расширенную матрицу системы - (m x (n + 1)) – матрицу
Чтобы определить ранг основной и расширенной матриц системы приведем к трапециевидному виду последнюю, используя для этого лишь элементарные преобразования строк. Этим преобразованиям адекватно отвечают аналогичные преобразования с соответствующими уравнениями системы и именно поэтому система «восстановленная» по последней трапециевидной матрице будет равносильна исходной. В случае совместности она и решается с помощью так называемого обратного хода, суть которого состоит в следующем: все неизвестные, если таковые имеются, коэффициенты которых не вошли в угловой базисный минор переносятся в правую часть и обзываются свободными или параметрическими. Оставшиеся в правой части неизвестные при этом называются базисными. Последнее k – ое уравнение решается относительно хк и это решение подставляется во все оставшиеся уравнения системы. После этого процедура повторяется для хк-1, хк-2 и так далее, до нахождения «последнего» - х1. Конечно же если ранг основной и расширенной матриц равен числу неизвестных системы, то все эти неизвестные будут базисными и система в таком случае имеет единственное решение. Если же число неизвестных превосходит этот ранг то все базисные будут выражены через какое то количество свободных, которым можно будет придавать произвольные значения, почему система и будет иметь бесчисленное множество – «пространство» решений. Количество свободных неизвестных определяет размерность этого пространства. Примеры: 1)
2)
3)
ВЕКТОРНАЯ АЗБУКА Основные определение и обозначения
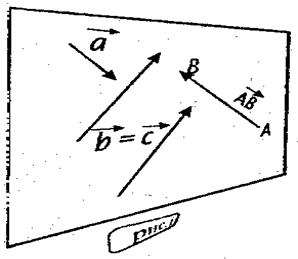
Будем называть вектором направленный отрезок, т.е. «объект», наделенный длиной - модулем и направлением - определенной внутренней (стрелка от начала к концу) и внешней (в пространстве) ориентацией.
Векторы принято обозначатьстрочными соответственно Векторы принято называть коллинеарными, если они параллельны одной, прямой и компланарными, если они параллельны одной плоскости. Ноль – вектор (
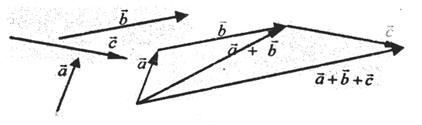
Линейные действия с векторами. 1. Произведением вектора 2. Суммой векторов 1) 3) λ (α
Вектор Линейная комбинация называется нулевой, если Линейная комбинация называется тривиальной(простейшей), если все её коэффициенты равны нулю. Очевидно, что тривиальная линейная комбинация является нулевой комбинацией. На предыдущем рисунке приведены примеры ненулевых линейных комбинаций. Теперь дадим очень важное определение.
Векторы
Базис и координаты.
Базисомвекторного пространства (множества векторов «на плоскости» или множество векторов «всего» пространства) будем называть любой упорядоченный максимальный набор линейно независимых векторов из этого пространства. Так, базисом на плоскости будет любая упорядоченная пара
Назовем координатами вектора в данном базисе коэффициенты(компоненты) его разложения по векторам базиса, записывая это так:
Из свойства линейных операций с векторами следует основное свойство координат вектора, состоящее в том, что линейным операциям с векторами отвечают те же операции с их координатами, то есть при сложении векторов их соответствующие координаты складываются, а при умножении вектора на число - все его координаты на это же число и умножаются. Декартовым прямоугольным базисом в пространстве ( на плоскости) будем называть упорядоченную тройку (пару) единичных и взаимно перпендикулярных векторов
Система координат «точечного» пространства.
Будем называть декартовой прямоугольной системой координат «агрегат», состоящий из фиксированной точки О - начала координат и декартового базиса
С помощью основного свойства решается и важная практическая задача как
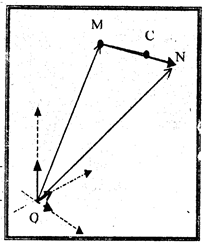
Задача о делении отрезка в данном отношении.
По данному «отношению»
координаты концов М и N которого известны найти координаты «точки деления» С.
Решение этой задачи:
формулы деления отрезка в данном отношении вытекает из лекго доказываемого векторного равенста

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ; ВТ = (2 1 0); С =
; ВТ = (2 1 0); С =  ; СТ =
; СТ = 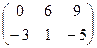 .
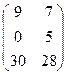
. + 3 ·
+ 3 ·  =
= 
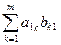
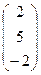 = (2 – 5 – 6) = (-9).
= (2 – 5 – 6) = (-9).
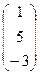 · (10 -11) =
· (10 -11) =  ;
; ·
·  =
= 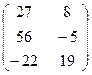 ;
;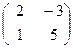 ·
· 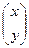 =
= 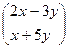
 ) – матрица Е, элементы которой
) – матрица Е, элементы которой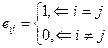
 ·
·  =
= 
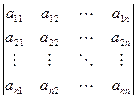

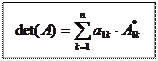

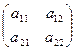 : М*11 = а 22, М*12 = а 21 А*11 = (-1)2 · М*11 = а 22,
: М*11 = а 22, М*12 = а 21 А*11 = (-1)2 · М*11 = а 22,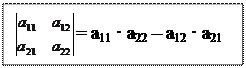
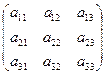 : М*11 =
: М*11 = 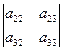 , М*12 =
, М*12 = 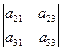 ,
,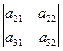 , А*11 = М*11, А*12 = - М*12, А*13 = М*13, а значит
, А*11 = М*11, А*12 = - М*12, А*13 = М*13, а значит 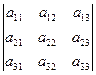 = а11 ·
= а11 · 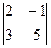 = 10 – (3) = 13;
= 10 – (3) = 13; 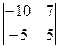 = - 50 – (-35) = -15;
= - 50 – (-35) = -15; 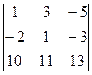 = 1 ·
= 1 ·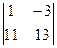 - 3 ·
- 3 · 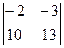 + (-5)·
+ (-5)· 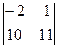 = (13+33) – 3 · (-26+30) – 5(-22-10) = 194.
= (13+33) – 3 · (-26+30) – 5(-22-10) = 194.
 . Раскладывая этот определитель по первой, второй и третьей строке последовательно получаем:
. Раскладывая этот определитель по первой, второй и третьей строке последовательно получаем: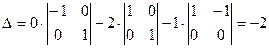
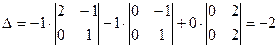 .
.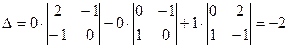
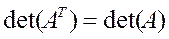
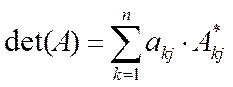
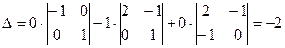
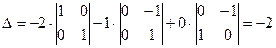 .
.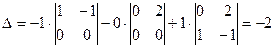

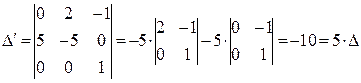
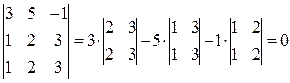 .
.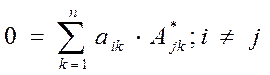

 - матрица, состоящая из алгебраических дополнений А*ij к соответствующим элементам а*ij.
- матрица, состоящая из алгебраических дополнений А*ij к соответствующим элементам а*ij.
 ,
,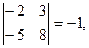 А*11 = 8, А*12 = 5, А*21 = -3, А*22 = -2,
А*11 = 8, А*12 = 5, А*21 = -3, А*22 = -2,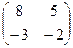 , В-1 = -
, В-1 = - 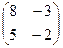 =
= 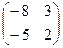 .
. .
.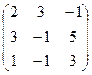 , ∆ =
, ∆ = 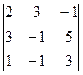 = -6,
= -6, , С-1 = -
, С-1 = -  ,
, .
.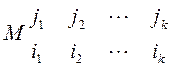 ,
, ,
,  ,
,  ,
,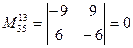 ,
, 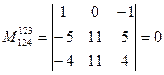 .
.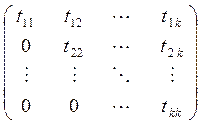

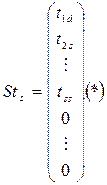
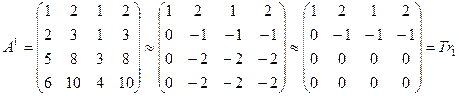
 (*)
(*)
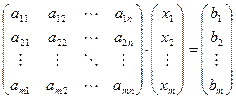
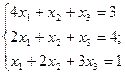 А-1 =
А-1 = 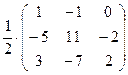 ; Х =
; Х = 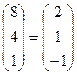 .
.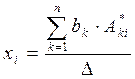 .
.
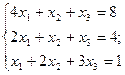
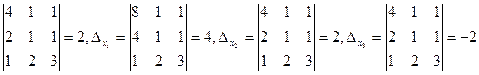
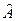 , полученную из главной добавлением столбца свободных членов. Сразу скажем, что вопрос о совместности системы решает
, полученную из главной добавлением столбца свободных членов. Сразу скажем, что вопрос о совместности системы решает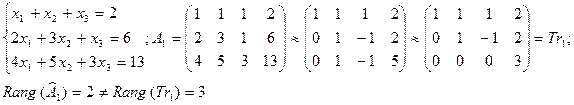
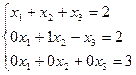

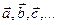 или двумя заглавными
или двумя заглавными  (первая - начало, вторая - конец) латинскими буквами со «стрелкой» над ними, а изображать - отрезок со стрелкой (рис. 1). Длины обозначаются
(первая - начало, вторая - конец) латинскими буквами со «стрелкой» над ними, а изображать - отрезок со стрелкой (рис. 1). Длины обозначаются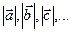 или
или 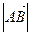 . Векторы естественно принято считать равными (одинаковыми) и не различать, если они имеют одинаковую длину и со направлены, т.е. при совмещении начал «совпадают» и их концы.
. Векторы естественно принято считать равными (одинаковыми) и не различать, если они имеют одинаковую длину и со направлены, т.е. при совмещении начал «совпадают» и их концы.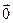 - вектор) начало и конец которого совпадают, принято считать коллинеарным с любым вектором (а значит, не имеющим направления).
- вектор) начало и конец которого совпадают, принято считать коллинеарным с любым вектором (а значит, не имеющим направления). на число λ будем называть вектор
на число λ будем называть вектор 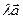 , со направленный при λ>0 и «антинаправленный» при λ<0 с вектором
, со направленный при λ>0 и «антинаправленный» при λ<0 с вектором  .
. будем называть вектор
будем называть вектор  =
= 
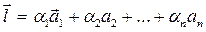 будем называть линейной комбинацией векторов
будем называть линейной комбинацией векторов 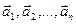 с коэффициентами
с коэффициентами  .
.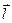 - ноль – вектор.
- ноль – вектор.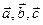 на соседнем рисунке линейно зависимы так как, очевидно
на соседнем рисунке линейно зависимы так как, очевидно  , а числа 2, 3, 1 - коэффициенты этой линейной зависимости. Отметим, что два вектора линейно зависимы, если они коллинеарны, а три - если они компланарны.
, а числа 2, 3, 1 - коэффициенты этой линейной зависимости. Отметим, что два вектора линейно зависимы, если они коллинеарны, а три - если они компланарны.
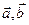 неколлинеарных векторов, а базисом в пространстве - упорядоченная тройка некомпланарных векторов
неколлинеарных векторов, а базисом в пространстве - упорядоченная тройка некомпланарных векторов 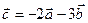
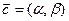 , если
, если  в базисе
в базисе 
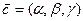 , если
, если 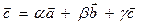 в базисе
в базисе 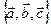 .
. (
(  ). Координаты векторов в таком базисе будем называть декартовыми координатами вектора в соответствующем базисе, обозначая их (x¸y¸z), ((х,у)). Итак,
). Координаты векторов в таком базисе будем называть декартовыми координатами вектора в соответствующем базисе, обозначая их (x¸y¸z), ((х,у)). Итак, 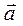 = (2,3) если
= (2,3) если 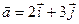 и
и 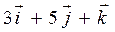 .
. наименовав его радиус – вектором точки М. Декартовы координаты (х,у,z) вектора
наименовав его радиус – вектором точки М. Декартовы координаты (х,у,z) вектора  называются декартовыми координатами точки М записывая это так: М (х,у,z). С помощью этого определения, с учетом основного свойства координат векторов, между прочим решается и обратная задача: по координатам начала М (хМ, уМ, zМ) и конца N(хN, уN, zN) так называемого привязанного вектора
называются декартовыми координатами точки М записывая это так: М (х,у,z). С помощью этого определения, с учетом основного свойства координат векторов, между прочим решается и обратная задача: по координатам начала М (хМ, уМ, zМ) и конца N(хN, уN, zN) так называемого привязанного вектора 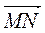 его координаты находятся так:
его координаты находятся так: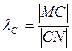 , в котором точка С делит отрезок MN,
, в котором точка С делит отрезок MN,