
|
|
Характеристический признак существования предела.
Свойства бесконечно малых. 1. Конечная сумма бесконечно малых есть бесконечно малая. 2. Произведение бесконечно малых на величину ограниченную есть бесконечно малая. С их помощью можно доказать Свойства переменных, имеющих предел
I. lim ( х + у) = lim х + lim у, II. lim ( х · у) = lim х · lim у, III. Если переменная в процессе изменения делается и остается больше любого задуманного положительного числа М, то она называется бесконечно большой переменной, что записывается так: lim у = ∞
Соответственно уточняются понятия Очевидно, что величины обратные бесконечно малым положительным переменными будут бесконечно большими переменными и наоборот.
Свойства бесконечно больших. 1. Сумма бесконечно больших переменных величин есть бесконечно большая переменная величина. 2. Произведение бесконечно больших п.в. на величину ограниченную есть бесконечно большая переменная величина. Однако, если х и у бесконечно большие п.в., а α и β бесконечно малые п.в., то ничего заранее нельзя сказать про значения:
Эти “не найденные” значения обозначают “неопределенностями” м обозначают соответственно К ней относился бы и второй замечательный предел: 1.
2.
3.
Заметим, что мы во всех примерах использовали “арифметические” свойства пределов лишь после уничтожения всех неопределенностей. Введем ещё несколько практически важных понятий. Прежде всего опишем
Сравнение бесконечно малых переменных величин. 1. Скажем, что бесконечно малые переменные величины α и β это б.м. одного порядка малости если
2. Скажем что α большего, чем β порядка малости если
3. Скажем что α и β - эквивалентные бесконечно малые, если
Обозначим последнее как α ≈ β. Примерами “замечательных” эквивалентных бесконечно малых являются в частности пары: Таблица замечательных эквивалентных бесконечно малых.
Характеристическое свойство бесконечно малых
Практически это свойтсво позволяет во многих случаях заменять при вычислении пределов одну бесконечно малую на эквивалентную ей другую бесконечно малую. Примеры 1. 2.
Непрерывность.
Как уже отмечалось, фукция у = (1+х)
то есть предел функции в этой точке существует. То же самое можно сказать и про функцию
Поэтому если доопределить последню в точке х0 = 0 значением 1, то есть считать что Функция 1. Существует 3.
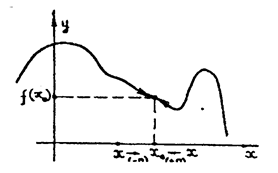
Для практической провекри функции на непрерывность первое условие делят на два: 1. а) существуют 1. б) существуют Тогда третье условие можно переписать так (рис. 1):
Пример: Проверить на непрерывность в точке х =2 функцию
1, а) 1, б) 2) f(2)=10 – 6 = 4, 3) “4 = 4 = 4” значит наша функция в точке х0 = 2 непрерывна.
В случае нарушения одного из перечисленных выше условий функция называется разрывной в точке х0. Положив
для R≠ 0, ∞ будем говорить, что в точке х0 функция имеет конечный разрыв или разрыв первого рода. Если R = 0, но f(x0) не существует, то разрыв называют устранимым. Если R = + (-) ∞ (или бесконечны оба “односторонних” предела), то разрыв в точке называется бесконечным или разрывом второго рода.
С бесконечными разрывами (и вообще пределами) связаны такие важные характеристики функции, как асимптоты. Забегая вперед, поговорим о них здесь.
Асимптоты функции
Различают вертикальные и наклонные (горизонтальные в частности) асимптоты. Прямая х – х0 = 0 - вертикальная асимтота, если хоть один из
Если прямая у = к х + в наклонная асимтота, то можно показать, что её параметры к и в находятся по формулам
(если к = 0, то асимтота горизонтальна).
Найти асимптоты графика функций а) вертикальная асимтота х = 0 (точка разрыва). Действительно б) для наклонной асимптоты
Итак, у= х - наклонная асимптота. График функции и ее асимптоты показаны на рисунке. Вернемся к разговору о непрерывности и скажем, что функция непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка (“в смысле” первого определения). Для непрерывных как в точке, так и на отрезке функций имеют место следующие Свойства непрерывных функций 1. Сумма и произведение непрерывных функций есть непрерывная функция. 2. Частное непрерывных функций есть непрерывная функция для всех точек в которых знаменатель отличен от нуля. 3. Функция непрерывная на отрезке: а ) ограничена; б) достигает на этом отрезке своих неибольшего и наименьшего значений; в) принимает на отрезке любое из промежуточных между своими наимельшим и наибольшем значение. 4. Если Последнее свойство может быть объяснено (и доказано) с помощью определения непреывности в точке, переписанного в следующей форме:
Из перечисленных свойств следует, что непрерывнымси являются функции
Производные фоункции
Пусть переменная х например, (аргумент функции), имевшая некое начальное значение х0, приняла значения х. Разность х – х0 назовем приращением переменной (аргумента) ч в точке х0 обозначив его ∆ х. Итак, по определению ∆ х = х – х0. Если функция у = f (х) определена как при х = х0, так и при х = х0 + ∆ х, то разность f (х0 + ∆ х) - f (х) ≡ ∆ у называют приращение функции у = f (х) в точке х = х0, которое отвечает приращению аргумента на ∆ х. Заметим, что как ∆ х, так и ∆ у могут быть как положительными, так и отрицательными величинами. Нетрудно увидеть, что если у = f (х) непрерывна в точке х0, то при ∆ х → 0 соответствующее ∆ у также стремится к нулю. Поэтому уверждение это принимается как второе определение непрерывности. Можно предположить, что величины ∆ у = f (х0 + ∆ х) – f (х) взятые для разных непрерывных в точке х0 функций и по “разному” вслед за ∆ х (“быстрее” или “медленее”), стремясь к нулю, несут в себе некую информацию о поведении функци в точке х0. Для выявления этой информации рассмотрим переменную величину
 ; ; 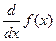 , по определению имеем: , по определению имеем:
Отметим три самых важных “смысла” производной функций, имеющих некую физическую или геометрическую “суть”. 1. Пусть замкнутый интервал [a¸x] обозначает кусок метериального неоднородного по массе, достаточно (чтобы пренебречь толщиной) тонкого стержны - “отрезка [a¸b] (рис. 3), а m (х) - масса этого куска (очевидно, m (а) = 0). Тогда величина
согласно известному физическому определению выражает плотность массы этого неоднородного стержны в точке. 2. Пусть t – время, а S (t) - зависимостьпути прямолинейного движения от времени (S (0=). Тогда физически очевидно, что
выражает мгновенную скорость этого прямолинейного движения в данный момент времени. 3. Рассмотрим график (γ) функции у = f (х) и определим касательную к этому графику (и вообще кривой) как предельное положение секущей (М0, М), кодга М “бежит” к М0 по (γ), если такое “положение” существует и не зависит от “стороны” на (γ) по которой М бежит М0 (см. рис.). Тогда, считая М имеет абсциссу х0 + ∆ х, и устремляя ∆ х к 0 (следи за рис. 4) имеем:
Итак, из определения следует, что величина
Пример. Написать уравнения касательных к графику функции у = х2 а) в точке с абсциссой х = 3; б) в произвольной ее точке х0. Итак, f (3) = 32, f (3+∆х)=(3+∆х)2. Тогда по определению
Таким обоазом, к = 6 и уравнение искомой касательной - у – 9 = 6 (х-3).
б) по определению
Таким образом, уравнение касательной к графику у = х2 в общем виде у – х02 = 2 х0 · (х – х0). По ходу решений примера сы выяснили, что производная функции х2 в любой фиксированной точке х (“без нолика”) равна 2х. Точно также можно показать, что (х3)' = 3 х2 и т.д. Это наводит на мысль о том, что производная любой функций - это некая вполне определенная для нее функция. Поэтому, чтобы для вычисления производных - “по научному - дифференцирования” - не прибегать каждый раз к определению - вычислению “скучных” пределов вполне естественно составить список - таблицу производных самых распространённых - элементарных функций. Для примера: 1.
2.
Перед тем как продолжить составление таблицы, приведем несколько общих правил дифференцирования. Прежде всего из свойств пределов легко следует, что если 1. 2. 3. 4. 5. Это, так сказать, «арифметические» правила дифференцирования. Однако правилом наиважнейшим, позволяющим превратить дифференцирование в алгебраическое действие - «исчисление», а некотором смысле схожее, например, с операцией умножения десятичных чисел «столбиком» является
Правило дифференцирования сложной функции В «старых» учебниках его еще называют «цепным» правилом. Итак если у = f (u), а u = φ (х), то есть у = f (φ (х)) - сложная - составная функция (композиция функций) то
где Примеры: 1.
2.
Отметим, что мы здесь брали «разные» композиции из одних и тех же функций, и результат дифференцирования естественно оказался зависимым от порядка «смешивания». Цепное правило естественным образом распространяется и на композицию из трех и более функций. При этом «звеньев» в «цепочке», составляющей производную будет соответственно три или более. Здесь и аналогия с умножением: «у нас» - таблица производных; «там» - таблица умножения; «у нас» - цепное правило а «там» - правило умножения «столбиком». При вычислении таких «сложных» производных никаких вспомогательных аргументов (u¸v и пр.), конечно же, не вводится, а, отметив для себя число и последовательность участвующих в композиции функций, «нанизывают» в указанном порядке соответствующие звенья. Примеры:
Следующими примерами будем «убивать пары зайцев»: потренируемся в дифференцировании сложных функций и дополним таблицу производных элементарных функций. Итак: 4. Для степенной функции - у = хα - переписав её с помощью известного «основного логарифмического тождества» - b=e ln b - в виде хα = хα ln x получаем
5. Для произвольной показательной функции применяя тот же приём будем иметь
6. Для произвольной логарифмической функции используя известную формулу перехода к новому основанию последовательно получаем
7. Чтобы продифференцировать тангенс (котангенс) воспользуемся правилом дифференцирования частного:
Для получения производных обратных тригонометрических функций воспользуемся соотношением которому удовлетворяют производные двух взаимообратных функций, то есть функций φ (х) и f (х) связанных соотношениями:
Вот это соотношение
Именно из этой формулы для взаимно обратных функций
8. Под конец сведём эти и некоторые другие, так же легко получаемые производные, в следующую таблицу.
Дифференциал функции.
Переобзовем приращение независимой переменной х дифференциалом этой переменной, обозначив его как dx, то есть для независимой переменной по определению будем считать
Теперь
Обозначив его символом dy или df (х) по определению будем иметь
Последняя формула называется «формой» «первого» дифференциала. Забегая вперед приведём и объясним «архиважнейшее» свойство дифференциала - так называемую инвариантность (неизменность) его формы. Итак
Действительно, пусть
Поэтому
то есть опять имеет ту же форму.
Однако «суть» (а не форма) дифференциала в этих двух случаях разная. Чтобы это объяснить выясним сначала геометрический смысл дифференциала и некоторые другие его свойства. Из приведенного ниже рисунка видно, что дифференциал является частью приращения ∆у. Можно показать, что dy, есть главная и линейная часть ∆у. Главная в том смысле, что разность ∆у – dy есть величина бесконечно малая высшего, что ∆х порядка малости, а линейная в смысле линейности Можно сказать также, что дифференциал есть (смотри рисунок) соответствующее приращение ординаты касательной. Теперь объяснима и разница в сути и значении дифференциальной формы при независимом и зависимом аргументе. В первом случае dx есть все приращение ∆х. С помощью определения легко доказываются и Арифметические свойства дифференциала 1. Определим теперь

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 где
где  .
.

 ;
;  ;
;  ;
; ;
;  ;
;  .
. Кроме них есть еще одна “замечательная” неопределенность, обозначаемая символом
Кроме них есть еще одна “замечательная” неопределенность, обозначаемая символом  . Это “ещё” на найденный
. Это “ещё” на найденный  , где
, где  .
. до его вычисления. Проиллюстрируем правила раскрытия неопределенностей несколькими примерами:
до его вычисления. Проиллюстрируем правила раскрытия неопределенностей несколькими примерами:
 ,
, .
. & ∞
& ∞ .
. .
.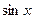 и
и  ,
,  и
и 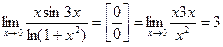 ,
,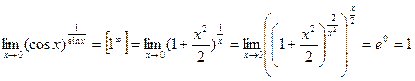 .
.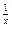 не определена в точке х0 = 0, однако
не определена в точке х0 = 0, однако ,
, :
:  - не существует, но
- не существует, но .
.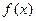 непрерывна в точке х = х0, если:
непрерывна в точке х = х0, если: ; 2. Существует
; 2. Существует  ;
;
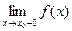 - (предел “слева”) и
- (предел “слева”) и - (предел “справа”).
- (предел “справа”).
 =
= 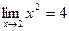 ,
, =
=  = 10 – 6 = 4,
= 10 – 6 = 4, то есть если х0 - точка разрыва второго рода.
то есть если х0 - точка разрыва второго рода. ,
, 

 :
: ;
; ,
,  .
. и
и  - непрерывны функции, то их композиция - сложная (стоставнаяяя0 функция
- непрерывны функции, то их композиция - сложная (стоставнаяяя0 функция  - также непрерывна на соответствующем отрезке.
- также непрерывна на соответствующем отрезке.
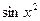 ,
, 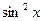 ,
,  ,
,  и подобные.
и подобные. и вычмслим ее предел при ∆ х → 0, обозвав этот предел производной функции. Итак
и вычмслим ее предел при ∆ х → 0, обозвав этот предел производной функции. Итак
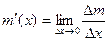

 ;
;  .
.
 это угловой коэффициент касательной (р) к графику (γ) в точке М0. Отсюда уравнение этой касательной можно записать так:
это угловой коэффициент касательной (р) к графику (γ) в точке М0. Отсюда уравнение этой касательной можно записать так:


 .
.
 - дифференцируемые функции, а С - константа, то
- дифференцируемые функции, а С - константа, то ;
; ;
; ;
; ;
; .
.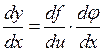
 , после вычисления рассматривается при u = φ (х).
, после вычисления рассматривается при u = φ (х). . Здесь у = u2; u=sin x. Тогда
. Здесь у = u2; u=sin x. Тогда .
. . Теперь
. Теперь  . Тогда
. Тогда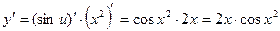 .
.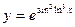 . Здесь с «иксом» для получения значения «игрека» проделывают пять операций , то есть, имеет место композиция из пяти функций: «внешняя» (последняя из них) - показательная - е ©; далее в обратном порядке степенная . (♦)2; тригонометрическая sin (?); степенная. ()3 и наконец логарифмическая ln.(Ë). Поэтому
. Здесь с «иксом» для получения значения «игрека» проделывают пять операций , то есть, имеет место композиция из пяти функций: «внешняя» (последняя из них) - показательная - е ©; далее в обратном порядке степенная . (♦)2; тригонометрическая sin (?); степенная. ()3 и наконец логарифмическая ln.(Ë). Поэтому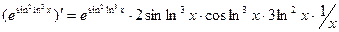 .
. .
. .
. .
. .
.

 и
и  ,
, , получаем
, получаем 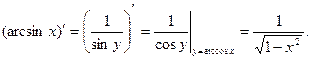






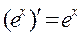
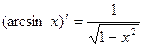









 , то есть у - сложная функция «от t» По определению дифференциала имеем
, то есть у - сложная функция «от t» По определению дифференциала имеем  . Но
. Но .
. ,
,
 своей зависимости от ∆х.
своей зависимости от ∆х. ; 2.
; 2.  ; 3.
; 3.  .
.