
|
|
Производные функции многих переменных.
Зафиксировав одну из переменных (х, у), например у, и «придав» приращение ∆х первой - х -, вычислим величину
обозвав ее «частным приращением по х,». Тогда
Обозначают такие частные производные одним из символов
Итак, по определению
Аналогично определяется частное приращение по у Из определения частных производных следует, что их «нахождение» сводится к «обычному» дифференцированию данной функции, как функции одной «выделенной» переменной при условии, что все остальные переменные «временно» считаются константами, «со всеми вытекающими из этого последствиями».
Примеры: 1. 2. Попутно упомянем здесь о таком важном понятии, как градиент. Градиентом функции двух переменных (или скалярного поля) называют лежащей на плоскости Оху вектор
Началом этого вектора, естественно, считается точка в которой вычисляются соответствующие частные производные, например:

К важнейшим относится следующие свойство градиента:
Градисит перпендикулярен соответствующей линии уровня и указывает направление («путь»), в котором функция возрастает «наискорейшим» образом. Модуль градиента при этом равен скорости возрастания функции в направлении градиента или, что тоже самое, крутизну графика функции в этом направлении.
Пример: для функции Решение:
Дифференцирование неявных функций
С помощью частных производных вычисляются производные так называемых неявных функций. Говорят, что переменная у является неявной (неявно заданной) функция от переменной х, если эта зависимость определяется уравнение вида
Частные производные от неявной функций двух переменных -
, ,
Дифференциал функции двух переменных. Касательная плоскость и нормаль к поверхности.
Полный дифференциал функции z=f(x¸y) двух переменных мы определим как выражение вида:
Пример: z=x·y3;dz=y3·∆x+3xy2·∆y. Его компоненты - слагаемые обзываются соответствующими частными дифференциалами («по х» и «по у»). Как и дифференциал функции одной переменно величина dz является главной линейной частью так называемого полного приращения
где
Уравнение соответствующей нормали - прямой, перпендикулярной к касательной плоскости в точке касания можно записать так:
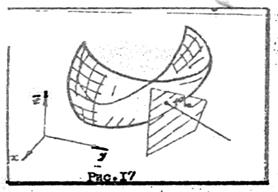
На рисунке условно изображены касательная плоскость и нормаль к графику некоторой функции в т. М0. Сравнивая уравнение касательной плоскости и соответствующий дифференциал функции, замечаем, что дифференциал (являясь главной частью полного приращения) выражает полное приращение аппликаты касательной плоскости к графику этой функции в данной точке.
Старшие производные
Так же как и для функции одной переменной, определяются вторые, третьи, ... .. «энные» частные производные. Правда, наличие двух и более переменных делает «букет» из них более богатым. Так, в частности, по определению и обозначению
Аналогичным образом определяется и производные более высокого порядка. Пример:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

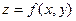 по х будем называть предел отношения частного приращения
по х будем называть предел отношения частного приращения  к приращению
к приращению  аргумента х при стремлении
аргумента х при стремлении 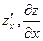 или
или  .
.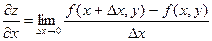
 данной функции и её частная производная
данной функции и её частная производная  по у.
по у. ;
; .
.
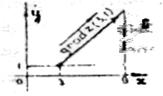

 найти линию уровня, проходящую через точку М0 (1,3) и крутизну графика функции в этой точке.
найти линию уровня, проходящую через точку М0 (1,3) и крутизну графика функции в этой точке. - линия уровня - окружность радиуса
- линия уровня - окружность радиуса  ;
; ;
; - крутизна графика функции - поверхности так называемого параболоида в точке М0.
- крутизна графика функции - поверхности так называемого параболоида в точке М0.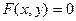 , то есть уравнением не разрешенным относительно у. Точно также можно говорить, что уравнение вида
, то есть уравнением не разрешенным относительно у. Точно также можно говорить, что уравнение вида 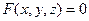 определяет неявно заданную функцию «z от х и у», то есть неявную функцию двух переменных. Можно показать, что в первом случае - для неявной функции «у от х» - производная «от у по х» находится по формуле.
определяет неявно заданную функцию «z от х и у», то есть неявную функцию двух переменных. Можно показать, что в первом случае - для неявной функции «у от х» - производная «от у по х» находится по формуле.
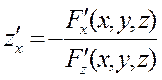
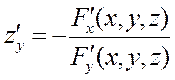

 и связан с ним соотношением
и связан с ним соотношением
 , а γ - некая бесконечно малая. Используя геометрический смысл частных производных, показывается, что для поверхности - графика функции z=f(x¸y) уравнение касательной плоскости в произвольной ее точке М0(х0, у0, f(x0¸y0)) можно записать в виде
, а γ - некая бесконечно малая. Используя геометрический смысл частных производных, показывается, что для поверхности - графика функции z=f(x¸y) уравнение касательной плоскости в произвольной ее точке М0(х0, у0, f(x0¸y0)) можно записать в виде
 .
.
 - вторые «смешанные» производные.
- вторые «смешанные» производные.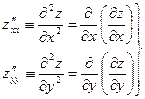 - вторые «чистые» производные.
- вторые «чистые» производные.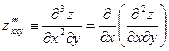 - третья смешанная производная.
- третья смешанная производная.
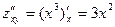 ;
;  ,
,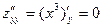 ,
,  ,
,  , ...
, ...