|
|
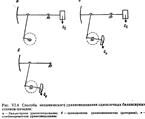
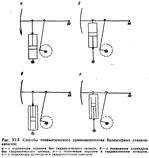
Балансирные станки-качалкиСтанки-качалки с двуплечным балансиром выполняются по кинематической схеме, приведенной на рис. VI. 1. При этом опора балансира (точка С) находится между точками подвеса штанг D и сочленения балансира с шатуном В. Усилия к балансиру могут передаваться несколькими способами. Наиболее часто для этого используются два шатуна, соединенные с балансиром траверсой. Механические балансирные станки-качалки снабжаются гравитацион-ным (т. е. грузовым) или пневматическим уравновешивающим устройством. Существуют следующие способы размещения уравновешивающего груза: на балансире, на кривошипе, на балансире с кривошипом, на шатуне. Соответственно приводы называют: станки качалки с балансирным, роторным, комбинированным и шатунным уравновешиванием. Станки-качалки с одноплечным балансиром уравновешиваются грузовым или пневматическим аккумулятором. В первом случае груз может монтироваться на балансире, кривошипе или на балансире и кривошипе одновременно. Уравнове-шивание соответственно называется: балансирное, роторное или комбини-рованное (рис. VI.4). Наибольшее применение получила схема с роторным уравновешиванием. Она отличается компак-тностью, что позволяет сконструировать менее металлоемкий привод. При пневматическом уравнове-шивании станок-качалка снабжается пневмо-цилиндром с ресивером и вспомогательным оборудованием. Уравновешивание достигается за счет накапливания потенциальной энергии пневматическим аккумулятором. Пневматическое уравновешивающее устройство хорошо вписывается в кинематическую схему станка-качалки (рис. VI.5) и имеет лучшие весовые и эргономические показатели по сравнению с грузовым.
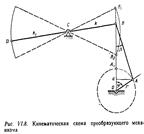
Безбалансирные механические приводы.Наиболее близкой по кинематической схеме к описанным установкам является СК, в котором балансир с шатуном заменяются гибкой подвеской (как правило, канатом), переброшенной через шкив, причем один ее конец соединяется с кривошипом, а второй—с устьевым штоком. Перемещение колонны насосных штанг в безбалансирных станках-качалках обеспе-чивается посредством гибкого звена — нес-кольких канатов, соединяющих кривошипы редуктора с траверсой, к которой подвешен устьевой шток. Кинематика балансирного станка-качалки: Каждое положение точки подвеса штанг характеризуется вполне определенными скоростями и ускорениями, которые (при постоянной частоте вращения ведущего вала редуктора) зависят только от размеров или же от соотношения размеров отдельных звеньев трансмиссии, преобразующего механизма. Преобразующий механизм балансирных станков-качалок представляет собой простейший плоский механизм первого класса второго порядка (рис. VI.8). Обозначим: кривошип отрезком ОА длиной r, шатун отрезком АВ длиной l, заднее ВС и переднее СД плечи балансира с длинами соответственно k и k1, база—расстояние между точками О и С длиной p. Известны три способа определения законов движения элементов балансирного станка-качалки. Эти способы в зависимости от принимаемых допущений позволяют с различной степенью точности найти закон изменения перемещения, скорости и ускорения точки подвеса штанг D.
Так называемая элементарная теория основана на следующих допущениях: преобразующий механизм станка-качалки рассматривается как обычный кривошипно-шатунный (т. е. r/l=0; r/k-=0). Отсюда следует, что точка B движется по прямой b1, B2, a Ðb=0. В этом случае закон движения точки B, а следовательно, и ТПШ D может быть определен с помощью теории кривошипно-шатунного механизма. Заметим, что изменение перемещения, скорости и ускорения ТПШ при использовании перечисленных допущений будут подчиняться простым гармоническим законам. Приближенная методика основывается на допущении, что r/k=0, траектория движения точки В—прямая, т. е. по существу также является теорией кривошипно-шатунного механизма, в котором учитываются конечные величины соотношения r/l. Точная методика не содержит допущений, принятых в рассмотренных ранее теориях, кроме одного, принятого ранее и специально не оговоренного: мгновенная угловая скорость вращения кривошипа постоянна и неизменна в течение всего двойного хода точки подвеса штанг. Точные законы изменения перемещения, скорости и ускорения точки подвеса штанг могут быть получены двумя способами: аналитическим—искомые величины определяются посредством тригонометрических преобразований и графически— построением положений механизма, планов скоростей и ускорений для различных углов поворота кривошипа (рис. VI.9). Приближенная и элементарная методики Найдем интересующие нас закономерности, рассмотрев кинематическую схему (см. рис. VI.8) и приняв допущения, соответствующие приближенной методике. Длина пути SB, пройденная точкой В при повороте кривошипа на угол j, равна отрезку B1B. Спроектировав точку А на вертикаль B1O, получим B1B=OB1-OB, где OB1=r+l, а величина OB=Oa+аВ. Величины Оа и аВ могут быть найдены из прямоугольных треугольников ВаА и ОаА: Ba=l*cosb, Oa=r*cosj. Окончательно можно записать: SB=r+l-(l*cosb+r*cosj)=r(1-cosj)+l(1-cosb) По теореме синусов для треугольников ОАВ следует, что r/sin b = l/sinj , откуда sinb= (r/l) sinj. Так как cosb=
Искомое перемещение точки D определяется, исходя из перемещения точки В с учетом соотношения плеч балансира k1/k. Скорость движения точкя D получим, продифференцировав это уравнение:
Ускорение движения точки D определим, еще раз продифференцировав уравнение:
Полученные формулы достаточно просты и могут использоваться для приближенных вычислений с приемлемой для практики точностью. С их помощью нетрудно определить, что максимальный путь SD будет при wt =180°, т. с. длина хода точки подвеса штанг SD max=2rk1/k, что максимального значения скорость достигнет при углах поворота кривошипа wt=90, 270° и будет равна VD max = ± wSmax/2. Максимальное ускорение будет при wt=00, 180° и равно
Уравнения описывают закон движения точки подвеса штанг при допущении, что траектория движения точки В—прямая. Если пренебречь также и величиной отношения r/l, как это принимается в элементарной методике, то из полученных зависимостей после подстановки в них r/l=0, получим
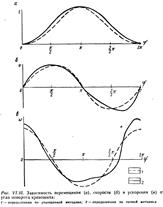
Из анализа этих зависимостей следует, что для балансирного станка-качалки, у которого длина радиуса кривошипа очень мала по сравнению с длиной шатуна и балансира, закон движения точки подвеса штанг является гармоническим (рис. VI. 10).
Гармонический закон движения точки подвеса штанг (кривые обозначенные пунктиром)—своеобразный эталон, с которым сравнивают фактические законы движения точек подвеса штанг, отличающиеся от гармонического в силу конечных длин элементов преобразующего механизма и ряда других факторов, например неравномерности вращения кривошипа. Таким образом, при анализе приближенных формул можно убедиться, что закон движения точки подвеса отличается от гармонического в сторону увеличения максимальных ускорений. Причем это отличие тем больше, чем больше соотн-ние r/l

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , то, подставив значение синуса и используя приближенную формулу для извлечения корня, получим
, то, подставив значение синуса и используя приближенную формулу для извлечения корня, получим  Подставив полученное значение в исходную формулу для SB и заменив j=w t, получим
Подставив полученное значение в исходную формулу для SB и заменив j=w t, получим .
.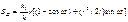
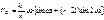
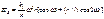

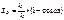
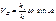
 (VI.4),
(VI.4),