|
|
Доказательство достаточных условийПусть
Теорема доказана. Снова рассмотрим систему (1.4). Если Определение 1.19. Рангом совместной системы линейных алгебраических уравнений называется ранг ее матрицы Предположим, что система (1.4) совместная и ранг ее равняется . Отделим в матрицы системы (1.4) некоторый базисный минор . Без ограничения общности соображений можно предположить, что он состоит из первых строк и первых столбцов матрицы , то есть:
В расширенной матрице
Помножим первое уравнение системы на При этом получим:
В соответствии с (1.7) это эквивалентно
Таким образом, любое уравнение системы (1.4) является линейной комбинацией первых базисных уравнений. То есть любое уравнение есть следствием базисных уравнений. Таким образом, система, которая складывается только из базисных уравнений, эквивалентная исходной системе (1.4). Эта система имеет вид
Итак, вместо системы (1.5) можно решать систему (1.8), которая состоит только из линейно независимых (базисных) уравнений. Сравним ранг СЛАУ Вариант, когда Вариант, когда
Систему (1.9) можно рассматривать как систему уравнений с неизвестными. Определитель системы Таким образом, для каждого конкретного набора значений Заметим, что при этом переменные Приведенные соображения доказывают такие утверждения. Утверждение 1.1. Система линейных алгебраических уравнений имеет одно- единственное решение, если ранг совместной системы равняется числу неизвестных Утверждение 1.2. Система линейных алгебраических уравнений имеет бесчисленное множество решений, если ранг совместной системы меньше числа неизвестных На практике процедуру исследования систем линейных алгебраических уравнений проводят следующим образом.
Пусть система уравнений задается соотношением (1.4). Дальнейшие исследования проводят с расширенной матрицей системы:
Очевидно, что в данном случае имеет место соотношение
Тогда соответствующая эквивалентная система будет представлена в виде:
В таком случае задача исследования системы состоит в том, чтобы описать ее общее решение. Для этого необходимо базисные переменные выразить через свободные. Итак, имеем
Последнее соотношение и определяет общее решение системы. Положив свободные сменные равными нулю,
Непосредственно процесс исследования системы проиллюстрируем на примере.
Задача1.9. Выполнить общее исследование системы линейных алгебраических уравнений
Решение 1. Выпишем расширенную матрицу системы и выполним соответствующие гауссовые исключения.
2. На основании анализа матрицы
получим: а) ; . Таким образом, и исходная система совместная; б) ; . Итак, исходная система будет иметь бесчисленное множество решений, и ее исследование будет состоять в том, чтобы описать это множество; в) исходная система имеет две 3. На основании матрицы
можно записать систему, эквивалентную исходной:
Очевидно, что за базисные переменные следует принять переменные 4. Опишем общее решение исходной системы
5. Проверку правильности найденного решения выполним по одному из базисных уравнений системы, например, по первому:
Итак, общее решение системы найдено верно. 6. Опишем некоторую совокупность частных решений. Для этого свободным переменным
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
. Рассмотрим базисных столбцов матрицы ; они будут базисными столбцами и для матрицы 
. Пусть это будут столбцы 
, 
, …, 
. В соответствии с теоремой о базисном миноре всякий столбец матрицы есть линейной комбинацией ее базисных столбцов. Это означает, что для столбца свободных членов будет справедливой равенство
.
, то такая система несовместная. Пусть 
.
.
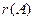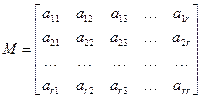. (1.6)
базисными строками, которые отвечают этому минору, будут первые строк. В соответствии с теоремой о базисном миноре всякая строка матрицы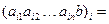 
(1.7)
, второе на 
, …, на 
и сложим их между собою. Причем отделим слагаемые, которые содержат 
, 
, …, 
.
.
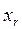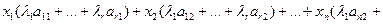
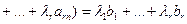
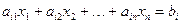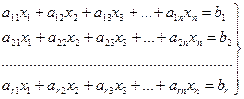(1.8)
с количеством неизвестных. Очевидно, что возможно только два варианта: или 
, или 
. Рассмотрим их.
.Итак, если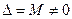 
и будет иметь единственное решение.
.В системе (1.8 )предоставим неизвестным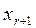 
, 
, …, 
произвольные числовые значения 
, 
, …, 
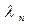и перенесем их в правую часть. В таком случае система (1.8) будет иметь вид:
(1.9)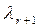
, 
система имеет единственное решение. Тем не менее разных наборов значений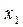 
, 
, …, 
. Итак, тогда система уравнений будет иметь бесчисленное множество решений.
.
.
.
(
(
, 
, …, 
и вычислив значения базисных переменных, получают одно из частных решений исследуемой системы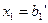
; 
; … ; 
,
, 
.
.
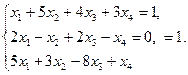
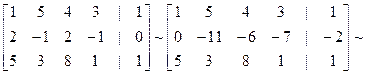
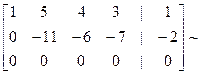
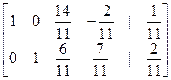
базисные переменные и две 
свободные переменные.
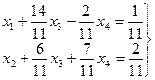
и 
, а свободными будут переменные 
и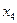 
.
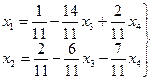
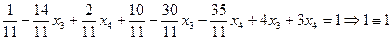
предоставим некоторые числовые значения и вычислим значения базисных переменных 
Результаты внесем в таблицу.