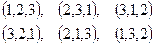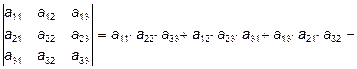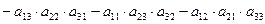|
|
Определитель квадратной матрицыКРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
(академічна різниця)
Холод О.Г., канд. техн. наук, доцент, Швачич Г.Г., канд. техн. наук, доцент
Раздел 1. ЛИНЕЙНАЯ АЛГЕБРА Тема 1.1. Матрицы. Действия над матрицами Определение 1.1. Матрицей размерности Согласно определению, матрица размерности
Числа Матрицу можно записать сокращенно в виде
где Определение 1.2. Матрица, все элементы которой равны нулю, называется нулевой.
Равенство матриц
Сравнивать можно только матрицы одинаковой размерности. Определение 1.3. Две матрицы Операции над матрицами
К операциям над матрицами относятся: сложение (вычитание) матриц, умножение матрицы на скаляр (число), умножение матриц. Сложение (вычитание) матриц Складывать (вычитать) можно только матрицы одной размерности. Определение 1.4. Суммой матриц
Аналогично определяется разность двух матриц. Заметим, что операция сложения (вычитания) матриц обладает теми же свойствами, что и операция сложения (вычитания) вещественных чисел. Умножение матрицы на число Определение 1.5. Произведением матрицы
То есть, при умножении матрицы на число, на это число умножаются все элементы матрицы. Умножение матриц Определение 1.6. Произведением матрицы
Другими словами, матрицу Задача 1.1. Найти произведение матриц
По правилу "строка–столбец" получим
Транспонирование матрицы
Определение 1.7. Транспонированием матрицы называется замена строк этой матрицы ее столбцами с сохранением их номеров. Матрица, полученная таким образом из матрицы Например, если Может оказаться, что квадратная матрица
Квадратная матрица
Если в матрице порядки
Для квадратной матрицы вводят понятие главной и побочной диагоналей. Главной диагональю квадратной матрицы называется диагональ, идущая из левого верхнего угла в правый нижний ее угол, побочной диагональю той же матрицы – диагональ, идущая из левого нижнего угла в правый верхний угол. Определение 1.8. Квадратная матрица, у которой все элементы, расположенные вне главной диагонали, равны нулю, называется диагональной. Определение 1.9. Диагональная матрица, у которой все элементы, стоящие на главной диагонали, равны единице, называется единичной и обозначается
С каждой квадратной матрицей связывают вполне определенную числовую характеристику, которая называется ее определителем или детерминантом. Определитель квадратной матрицы
Рассмотрим квадратную матрицу Определение 1.10. Определителем, соответствующим квадратной матрице – определитель – каждое слагаемое представляет собой произведение – слагаемое берется со знаком плюс, если число инверсий в перестановке вторых индексов сомножителей четное, и со знаком минус – в противном случае. Итак, по определению имеем:
В последней формуле суммирование распространяется на все перестановки Рассмотрим некоторые частные случаи. Пусть
Членом такого определения будет произведение вида:
где Следовательно,
Таким образом, определитель второго порядка, соответствующий квадратной матрице второго порядка, равен разности произведений элементов, стоящих на главной диагонали, и элементов, стоящих на побочной диагонали. Пусть
Членами определителя третьего порядка являются произведения вида:
Отметим, что первая группа перестановок имеет четное число инверсий, вторая – нечетное, поэтому:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
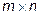 называется прямоугольная таблица из чисел, содержащая
называется прямоугольная таблица из чисел, содержащая  строк и
строк и 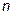 столбцов.
столбцов.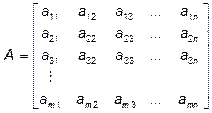 .
. , образующие матрицу, называются ее элементами. Индексы
, образующие матрицу, называются ее элементами. Индексы  и
и 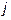 элемента
элемента  ,
,
 .
. называются равными, если они имеют одинаковые порядки, а соответствующие элементы равны между собой. Таким образом,
называются равными, если они имеют одинаковые порядки, а соответствующие элементы равны между собой. Таким образом, 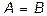 , если
, если  для всех значений
для всех значений 
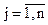 .
. того же порядка, элементы которой
того же порядка, элементы которой  определяются равенством
определяются равенством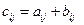 .
. на вещественное число
на вещественное число 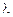 называется матрица
называется матрица  той же размерности, что и матрица А, элементы которой равны
той же размерности, что и матрица А, элементы которой равны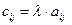 .
. , имеющей порядки соответственно равные
, имеющей порядки соответственно равные 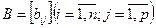 , имеющую порядки соответственно равные
, имеющую порядки соответственно равные 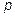 , называется матрица
, называется матрица  , имеющая порядки соответственно
, имеющая порядки соответственно  определяются по формуле
определяются по формуле (1.1)
(1.1)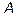 можно умножить на матрицу
можно умножить на матрицу  тогда и только тогда, когда числостолбцов матрицы
тогда и только тогда, когда числостолбцов матрицы  равен сумме попарных произведений соответствующих элементов
равен сумме попарных произведений соответствующих элементов  ,
, 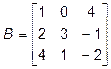
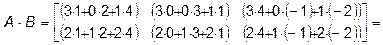
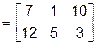
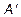 .
. , то
, то 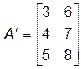
 . В этом случае матрица
. В этом случае матрица 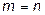 называется ее порядком. Квадратная матрица имеет вид
называется ее порядком. Квадратная матрица имеет вид .
. . Например,
. Например, .
.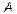 произвольного порядка. Определитель (детерминант) матрицы обозначается
произвольного порядка. Определитель (детерминант) матрицы обозначается  или
или  .
. элементов матрицы;
элементов матрицы;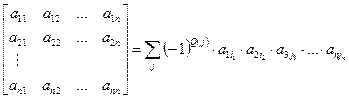
 , которые можно составить из чисел
, которые можно составить из чисел  .
. . В общем виде определитель второго порядка записывается следующим образом:
. В общем виде определитель второго порядка записывается следующим образом: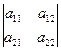 .
.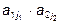
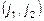 – любая перестановка из чисел 1, 2. Возможных перестановок две:
– любая перестановка из чисел 1, 2. Возможных перестановок две:  . В первом случае имеем
. В первом случае имеем 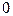 инверсий
инверсий  , а во втором – одну
, а во втором – одну  . Следовательно, в первом случае четное число инверсий, а во втором – нечетное.
. Следовательно, в первом случае четное число инверсий, а во втором – нечетное. .
. . Определитель третьего порядка имеет вид
. Определитель третьего порядка имеет вид .
. где
где  – перестановки из чисел
– перестановки из чисел 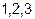 . Таких возможных перестановок шесть:
. Таких возможных перестановок шесть: