
|
|
Практическое правило вычисление определителей
При вычислении определителей широко используются формулы разложения по строке или столбцу (теорема Лапласа), а также свойство, позволяющее, не изменяя величины определителя, преобразовать его к такому виду, когда какой-либо ряд содержит максимально возможное число нулей. Именно этот ряд рационально принять в качестве ряда для разложения по Лапласу. Такой подход к вычислению определителей называется правилом понижения порядка.
Задача 1.2. Вычислить определитель
В качестве ряда для разложения рационально использовать вторую строку, которая содержит два нулевых элемента. Для уменьшения объема последующих вычислений можно добиться большего числа нулей в этой строке. Работать будем со столбцами. Сложим соответствующие элементы второго и третьего столбцов и запишем результат на месте третьего столбца.
Используя свойство 8, добавим к элементам второго столбца соответствующие элементы четвертого столбца, умноженные на число 2. Получим
Далее разложим определитель по элементам второй строки.
Теперь в определителе четвертого порядка добьемся наибольшего числа нулей в третьей строке. Для этого умножим на
Разложим определитель четвертого порядка по элементам третьей строки
В определителе третьего порядка добьемся наибольшего числа нулей во втором столбце. Будем работать со строками. Все элементы первой строки умножим на число
Применим теорему Лапласа, выбрав в качестве ряда для разложения второй столбец. Получим:
Наконец, вычисляя определитель второго порядка, окончательно имеем
Обратная матрица
Одно из важнейших свойств умножения чисел состоит в том, что для каждого числа
Оказывается, что нечто подобное имеет место и для матриц, причем роль условия Определение 1.13. Квадратная матрица называется невырожденной, если ее определитель не равен нулю Определение 1.14. Матрица
Условие существования обратной матрицы сформулируем в виде теоремы. Теорема 1.1. Для того, чтобы квадратная матрица Обратная матрица находится по следующей схеме: 1. Вычисляется определитель 2. Формируется матрица, составленная из алгебраических дополнений элементов
3. Транспонируют союзную матрицу, определяя тем самым так называемую присоединенную матрицу. Такая матрица обозначается
4. Обратная матрица
Задача 1.3. Дана матрица Вычислим определитель матрицы
Матрица невырождена, следовательно, обратная матрица существует. Найдем алгебраические дополнения элементов определителя.
Формируем союзную матрицу
Определим присоединенную матрицу
Найдем обратную матрицу
Ранг матрицы
Введем понятие минора матрицы. Рассмотрим некоторую матрицу
Выделим в этой матрице Среди миноров различных порядков матрицы есть равные нулю и отличные от нуля. Определение 1.15. Рангом матрицы Для определения ранга матрицы следует рассматривать все ее миноры наименьшего порядка и, если хоть один из них отличен от нуля, переходить к вычислению миноров более высокого порядка, включающих (окаймляющих) отличный от нуля минор предыдущего порядка. Такой подход к определению ранга матрицы называется методом окаймления (или методом окаймляющих миноров). Задача 1.4. Методом окаймляющих миноров определить ранг матрицы
Рассмотрим окаймление первого порядка, например, Например, Наконец, проанализируем окаймление третьего порядка
Таким образом, наивысший порядок минора, отличного от нуля, равен 2, следовательно,
Базисный минор матрицы
Определение 1.16. Базисным минором матрицы называется всякий, отличный от нуля минор этой матрицы, порядок которого равен рангу матрицы. Теорема 1.2. (Теорема о базисном миноре). Базисные строки (базисные столбцы) матрицы линейно независимы. Заметим, что строки (столбцы) матрицы линейно зависимы тогда и только тогда, когда хотя бы одну из них можно представить как линейную комбинацию остальных. Теорема 1.3. Число линейно независимых строк матрицы равно числу линейно независимых столбцов матрицы и равно рангу матрицы. Теорема 1.4. (Необходимое и достаточное условие равенства нулю определителя). Для того, чтобы определитель Вычисление ранга матрицы, основанное на использовании его определения, является слишком громоздкой операцией, так как связано с вычислением большого числа миноров различных порядков. На практике ранг матрицы находят с помощью элементарных преобразований. Эквивалентность матриц
Определение 1.17. Две матрицы Если матрицы Теорема 1.5. Ранг матрицы не меняется при элементарных преобразованиях. То есть элементарные преобразования – это такие преобразования, которые не приводят к изменению ранга матрицы. К ним относятся: – транспонирование матрицы, – перестановка параллельных рядов; – вычеркивание ряда, все элементы которого равны нулю; – умножение всех элементов какого-либо ряда на число, отличное от нуля; – добавление к элементам какого-либо ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число Следствие теоремы 1.5. Если матрица При вычислении ранга матрицы ее следует привести при помощи конечного числа элементарных преобразований к трапециевидной форме или к эквивалентной единичной матрице. Определение 1.18. Трапециевидной будем называть такую форму представления матрицы, когда в окаймляющем миноре наибольшего порядка, отличном от нуля, все элементы, стоящие ниже диагональных, равны нулю. Например:
Здесь Как правило, матрицы к трапециевидной форме приводят при помощи алгоритма Гаусса. Идея алгоритма Гаусса состоит в том, что, умножая элементы первой строки матрицы на соответствующие множители, добиваются, чтобы все элементы первого столбца, расположенные ниже элемента Задача 1.5. Определить ранг матрицы с помощью элементарных преобразований
Для удобства применения алгоритма Гаусса поменяем местами первую и третью строки
~
Очевидно, что здесь
~

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
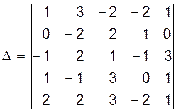
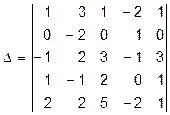
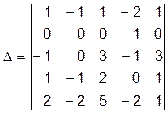
 .
. элементы первой строки и сложим их с соответствующими элементами третьей строки.
элементы первой строки и сложим их с соответствующими элементами третьей строки. .
. .
. и сложим с соответствующими элементами третьей строки
и сложим с соответствующими элементами третьей строки .
.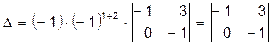 .
.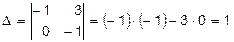
 , отличного от нуля, существует обратное
, отличного от нуля, существует обратное  такое, что
такое, что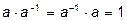 .
. играет условие, состоящее в том, что определитель матрицы
играет условие, состоящее в том, что определитель матрицы 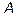 отличен от нуля.
отличен от нуля. . В противном случае
. В противном случае  матрица называется вырожденной.
матрица называется вырожденной.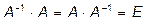 .
. исходной квадратной матрицы
исходной квадратной матрицы 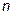 -го порядка.
-го порядка. исходной квадратной матрицы
исходной квадратной матрицы 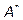 :
: .
. и выглядит следующим образом:
и выглядит следующим образом: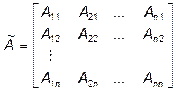 .
. по отношению к матрице
по отношению к матрице 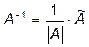 .
. . Найти обратную матрицу по отношению к заданной.
. Найти обратную матрицу по отношению к заданной. .
.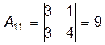 ;
;  ;
; 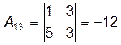 ;
; ;
;  ;
;  ;
; ;
;  ;
;  .
. .
. .
. .
. .
. произвольных строк и
произвольных строк и 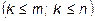 . Определитель
. Определитель 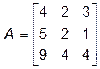 .
.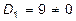 . Затем перейдем к рассмотрению некоторого окаймления второго порядка.
. Затем перейдем к рассмотрению некоторого окаймления второго порядка. .
. .
. .
. был равен нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы.
был равен нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы. называются эквивалентными, если их ранги равны, т.е.
называются эквивалентными, если их ранги равны, т.е.  .
. .
.

 .
.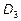
 , элементы матрицы
, элементы матрицы  обращаются в нуль. Тогда форма представления такой матрицы будет трапециевидной.
обращаются в нуль. Тогда форма представления такой матрицы будет трапециевидной.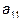 , обратились в нуль. Затем, умножая элементы второго столбца на соответствующие множители, добиваются, чтобы все элементы второго столбца, расположенные ниже элемента
, обратились в нуль. Затем, умножая элементы второго столбца на соответствующие множители, добиваются, чтобы все элементы второго столбца, расположенные ниже элемента  , обратились в нуль. Далее аналогично.
, обратились в нуль. Далее аналогично. .
.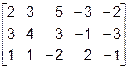 ~
~ 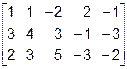 ~
~  ~
~ ~
~  ~
~  .
. ~
~  ~
~  ~
~  ~
~ ~
~ 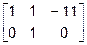 ~
~  ~
~ 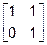 .
.