
|
|
Основные принципы метода анализа иерархий1. Принцип идентичности и декомпозиции.Предусматривает структурирование проблем в виде иерархии или сети. 2. Принцип сравнительный суждений (парных сравнений). Предполагает, что элементы задачи (альтернативы и критерии) сравниваются попарно с позиции их воздействия на общую характеристику. 3. Принцип синтеза приоритетов. Предполагает формирование набора локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня.
Постановка задачи (пример)
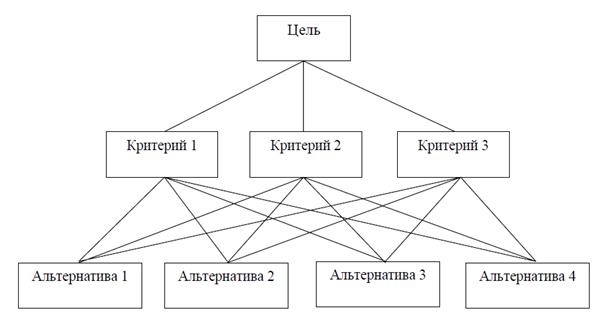
Целью задачи является строительство аэропорта [3]. Необходимо выбрать лучшую площадку для строительства аэропорта с точки зрения выделенных критериев. Комиссия по выбору постройки аэропорта предварительно отобрала из нескольких возможных три альтернативных варианта площадок – А1, А2, А3. Было выявлено три основных критерия, влияющих на принятие решения о выборе площадки для строительства: 1 – стоимость строительства, 2 – время в пути от аэропорта до центра города, 3 – количество жителей, подвергающихся шумовым воздействиям. При решении задачи используется МАИ для поддержки процесса принятия решений. Этапы МАИ Этап 1.Построение иерархической структуры задачи многомерного выбора. В общем случае простейшей трехуровневой иерархии структура имеет вид Рис.1
Рис. 1. Обобщенна иерархическая структура проблемы
Этап 1.Структуризация. Структуру решаемой задачи можно представить в виде иерархической структуры, показанной на Рис. 2.
Рис. 2. Иерархическая структура проблемы
Этап 2.Выполнение попарных экспертных сравнений элементов каждого уровня иерархий. Рассмотрим элементы С1, С2, …, Сn некоторого зафиксированного уровня иерархи. Мы хотим определить веса ѡ1, ѡ2, …,ѡn влияния этих элементов на некоторый элемент вышестоящего уровня. Основным инструментом оценки влияния является матрица чисел по шкале отношений 1, …, 9 (табл. 1), представляющих суждения о парных сравнениях. Для представления приоритетов в МАИ выбран собственный вектор, принадлежащий наибольшему собственному значению указанной матрицы А. Обозначим через
Матрица А с содержательной точки зрения будет согласованной по оценкам при введении условия
С математической точки зрения это условие наделяет матрицу А свойством обратносимметричной матрицы. На главой диагонали матрицы А стоят 1. Если оценки попарных сравнений известны точно, т.е. основаны на экспериментальных измерениях, то
т.е. веса влияния элементов известны. Например, если взвешиваются два предмета: С1=3052 и С2=2442. Тогда отношение Для случая экспериментального измерения весов ѡ1, ѡ2, …,ѡi,…, ѡn сравниваемых элементов на уровне иерархии согласованность считается полной, естественно, с точностью до погрешности измерительных приборов. При экспертной оценке отношений ( ) согласованность суждений и соответственно матрицы А будет не полной. Значит нужно разработать некоторую числовую меру отклонения согласованности матрицы А от идеальной (см. ниже формулу отношения согласованности ( )). Теперь рассмотрим подробнее содержательный смысл требования согласованности в МАИ. В МАИ под согласованностью суждений подразумевается не просто традиционное требование транзитивности предпочтений [3]: если для индивидуума яблоки предпочтительнее апельсинов, а апельсины предпочтительнее бананов, то яблоки должны быть предпочтительнее бананов. Схематически это можно записать так:
В МАИ транитивность наделяется количественными отношениями. Например, если яблоки в 2 раза предпочтительнее апельсин (например, по цене), а апельсины предпочтительнее бананов в 3 раза, то яблоки должны быть в 6 раз предпочтительнее бананов. Именно это автор МАИ Саати называет числовой (кардинальной) согласованностью предпочтений. Несогласованность означает отсутствие пропорциональности, которое может нарушить транзитивность. МАИ не только показывает наличие несогласованности отдельных сравнений, но и дает численную оценку того, как сильно нарушена согласованность для всей рассматриваемой задачи.
Замечание. В простейшей версии МАИ считается, что элементы в каждой группе иерархии (называемой уровнем, кластером, стратой) независимы между собой, но все они влияют на каждый элемент другого (вышестоящего) уровня. Таким образом, общая задача многокритериального выбора сводится к задаче оценки влияния уровней иерархи (снизу-вверх либо сверху-вниз).
Теперь обратимся к расчетам для нашего примера.
1. Зафиксируем нижний (третий) уровень иерархи Рис. 2, содержащий элементы А1, А2, А3 альтернативных площадок для строительства аэропорта. Зафиксируем также один элемент К1 – стоимость строительства на уровне 2 иерархии.
Примечание: в МАИ можно формировать матрицу парных сравнений на основе любой шкалы отношений, применяемой для измеряемых свойств сравниваемых объектов. В этом случае экспертная оценка заменяется отношением двух соответствующих измерений. Новая шкала (собственный вектор), которая выводится из матрицы парных сравнений, содержащий оценки реальных измерений, будет эквивалентна той, которую можно получить путем нормирования соответствующих измерений.
Таблица 1 Шкала относительной влажности
Матрица экспертных оценок влияния элементов А1, А2, А3 на элемент К1 второго уровня иерархии показана в таблице 2 (выделено темным цветом). В таблице 2 приведены также расчетные величины для определения максимального собственного значения Аналогично получены матрицы парных сравнений элементов А1, А2, А3 относительно критерия К2 (таблица 3) и критерия К3 (таблица 4).
Таблица 2 Матрица парных сравнений альтернатив по первому критерию
Таблица 3 Матрица парных сравнений альтернатив по второму критерию
Таблица 4 Матрица парных сравнений альтернатив по третьему критерию
Аналогично строиться матрица парных сравнений для второго уровня иерархий, элементами которого являются критерии К1, К2, К3. Эта матрица показана в таблице 5 (выделено темным цветом). матица сравнений критериев выбора площадки для аэропорта приведена в таблице 5. Таблица 5 Матрица парных сравнений критериев
Этап 3. Определение вектора приоритетов. В качестве вектора приоритетов для каждого уровня иерархии принят нормализованный главный собственный вектор матрицы попарных сравнений. Для расчета этих векторов используется приближенный метод 4 из [1] оценки через средние геометрические. Собственный вектор обеспечивает упорядочение приоритетов. Чем больше i-я компонента СВ, тем больше влияние i-го элемента в комплексе всех элементов анализируемого уровня иерархии на выделенный элемент С вышестоящего уровня. Для нижнего уровня альтернатив (площадок для строительства П1, П2, П3) алгоритм расчета собственного вектора, относящийся к матрице парных сравнений из таблицы 2, показан в таблице 6. В таблице 2 показан также результат расчета – нормализованный собственный вектор Аналогично рассчитывается нормализованные собственные векторы для матриц парных сравнений Ас.2 и Ас.3 из таблиц 3 и 4. Получены оценки: Для второго уровня иерархии, включающего критерии К1, К2 и К3, оценка нормализованного собственного вектора, характеризующие приоритеты этого уровня по влиянию на единственный элемент верхнего (первого) уровня, т.е. цель выбора, производится по описанному выше алгоритму. Для матрицы парных сравнений Ас.4 из таблицы 5, получены данные расчета: Таким образом, все векторы приоритетов для второго и третьего уровней иерархии получены.
Этап 4. Определение максимальных собственных значений и степени согласованности матриц парных сравнений. Прежде чем перейти к синтезу оптимальной альтернативы с учетом всех элементов второго и третьего уровней иерархии, нужно убедиться в достаточном уровне согласованности всех матриц суждений Ас.1, Ас.2, Ас.2, Ас.4. Для этого нужно вычислить максимальные собственные значения
где k – номер матрицы парных сравнений (суждений);
Таблица 6 Матрица парных сравнений альтернатив по первому критерию К1
В () умножение производится по правилу скалярного произведения векторов. Например, для матрицы суждений Ас.1 из таблицы 2 получим:
Максимальные собственные значения всех матриц суждения
Этап 5. Определение индексов согласованности и отношений согласованности для матриц суждений. В общем случае под согласованностью понимается то, что при наличии основного (базового) массива необработанных данных все другие данные логически могут быть получены из них. Или другими словами, отношения элементов всей матрицы А не должны быть противоречивыми. Из теории МАИ известно, что согласованность положительной обратносимметричной матрицы эквивалентна требованию
Заметим, что
Тогда степень согласованности матрицы суждений можно оценить мерой, называемой индексом согласованности (ИС)
Знаменатель Следовательно, ИС имеет смысл отклонения от абсолютной согласованности, приходящегося на одно парное сравнение. Вводится критерий, называемый отношением согласованности (ОС):
где СС – индекс случайной согласованности. СС определяется путем задания оценок по шкале отношений для случайно выбранных суждений
Таблица 7 Случайная согласованность для случайных матриц
Приемлемая величина ОС – порядка 10% или менее. Если ОС выходит из этих пределов, то ЛПР должно провести более глубокие исследования задачи и проверить свои суждения, т.е. назначение величин В качестве примера приведем оценки для матрицы суждений Ас.1 из таблицы 2:
Величины значения индекса согласованности и отношений согласованности для матриц суждений Ас.1, Ас.2, Ас.3, Ас.4 показаны соответственно в таблицах 2, 3, 4 и 5.
Замечание.Формально отношения согласованности ОС1=0,378 для матрицы Ас.1, ОС3=0,31 для матрицы Ас.3 и ОС4=0,26 для матрицы Ас.4 являются неприемлемыми, т.е. уровень их согласованности очень мал. Требуется, чтобы ОС было меньше 0,1. Однако исправление указанных матриц суждения, а значит и всей задачи мы делать не будем, поскольку рассматриваемая задача носит учебный характер.
Этап 6. Синтез приоритетов уровней. В математической теории иерархий разработан метод оценки воздействия уровня на соседний вышестоящий уровень путем композиции соответствующего вклада (приоритетов) элементов данного уровня по отношении к каждому элементу соседнего верхнего уровня. Композиция распространяется снизу-вверх. В принципе, можно рассматривать также распространение композиции сверху-вниз. Математически «композиция» отображается оператором умножения. Как известно [3] в математической логике операция умножения отображает совместное действие сомножителей. Приоритеты синтезируются, начиная со второго уровня вниз. Локальные приоритеты (приоритеты альтернатив П1, П2, П3 по каждому критерию) перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии критериями на которые воздействует этот элемент. Процедура продолжается до самого нижнего уровня. В формализованном виде процедура синтеза приоритетов имеет следующий вид. Общий вектор приоритетов взаимного влияния уровня 3 альтернатив (П1, П2, П3) и уровня 2 критериев (К1, К2, К3) на общую цель (уровень 1) равен:
где В – матрица компонент нормированных векторов приоритетов альтернатив первого уровня (см. таблицы 2, 3 и 4); В (9) умножение производится по правилам умножения матрицы на вектор:
Для нашего примера:
Этап 7. Выбор оптимально альтернативы. Алгоритм оптимального выбора прост:
Таким образом, алгоритм оптимального многокритериального выбора приводит к выбору площадки П1 для строительства аэропорта, так как ей соответствует наибольшее значение компоненты вектора общего приоритета
Достоинством метода анализа иерархий является направленность на сравнение реальных альтернатив. Метод может применятся в тех случаях, когда эксперты не могут дать абсолютной оценки альтернатив по критериям, а пользуются более слабыми сравнительными измерениями.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

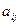 число (бал), соответствующее значимости (предпочтения) элемента Сi по сравнению с элементом Сj данного уровня иерархии по влиянию Сi, Сj на фиксированный элемент вышестоящего уровня (например К1 на Рис. 2):
число (бал), соответствующее значимости (предпочтения) элемента Сi по сравнению с элементом Сj данного уровня иерархии по влиянию Сi, Сj на фиксированный элемент вышестоящего уровня (например К1 на Рис. 2):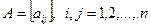 . (4)
. (4)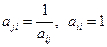 . (5)
. (5) , (6)
, (6) означает, что предмет С1 в 1,25 раз тяжелее предмета С2.
означает, что предмет С1 в 1,25 раз тяжелее предмета С2. .
.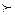 – знак предпочтения элемента в отношении двух элементов; ∩ – знак пересечения множеств (совместности).
– знак предпочтения элемента в отношении двух элементов; ∩ – знак пересечения множеств (совместности).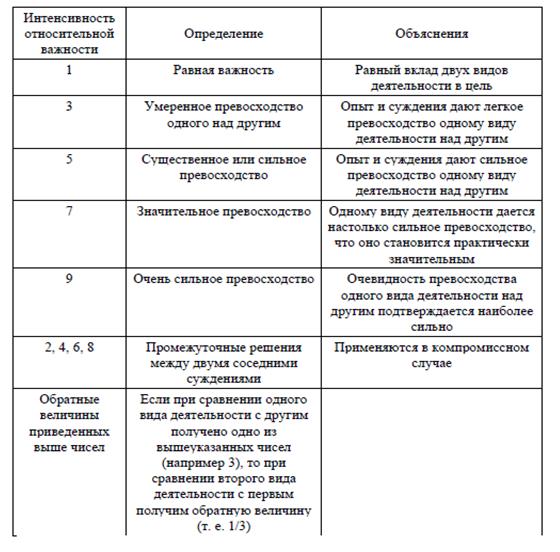
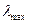 и главного собственного вектора
и главного собственного вектора  полученной матрицы А (алгоритм расчета этих величин описан в этапе 3 алгоритма).
полученной матрицы А (алгоритм расчета этих величин описан в этапе 3 алгоритма).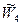
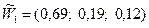 .
.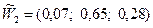 ;
;  , которые отражены в таблицах 3 и 4.
, которые отражены в таблицах 3 и 4.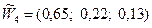 .
. ,
,  (7)
(7) – вектор-строка столбцовых сумм матрицы суждений с номером k;
– вектор-строка столбцовых сумм матрицы суждений с номером k; 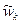 – нормализованный собственный главный вектор матрицы суждений Ас.k, принадлежащий наибольшему собственному значению
– нормализованный собственный главный вектор матрицы суждений Ас.k, принадлежащий наибольшему собственному значению 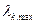 .
.
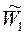

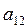
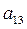

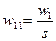


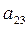
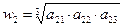


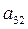
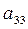
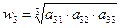

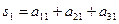
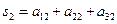
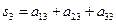
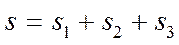
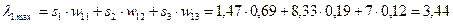 .
. ,
,  ,
, 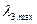 ,
, 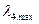 приведены соответственно в таблицах 2, 3, 4 и 5.
приведены соответственно в таблицах 2, 3, 4 и 5.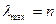 .
.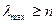 всегда верно, поэтому
всегда верно, поэтому .
.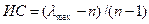 .
. – это число всех возможных парных сравнений данного элемента
– это число всех возможных парных сравнений данного элемента 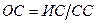 , (8)
, (8)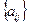 при парных сравнениях и соответствующих им обратных величин для матрицы А Значения СС в теории МАИ заранее вычислены и представлены в таблице 7.
при парных сравнениях и соответствующих им обратных величин для матрицы А Значения СС в теории МАИ заранее вычислены и представлены в таблице 7. ;
; .
.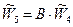 , (9)
, (9)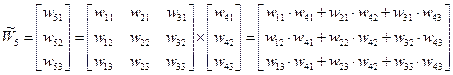 . (10)
. (10) .
. .
.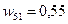 .
.