
|
|
Собственные векторы и собственные значения матрицы
Прежде, чем изложить подробно алгоритм МАИ и описать пример его применения, приведем элементарные сведения о понятиях «собственный вектор» (СВ) матрицы и ее «собственное значение» (СЗ), поскольку МАИ основан на использовании этих понятий и математическим аппарате линейной алгебры.
Определение. Число λ называется собственным значением (или характеристическим числом) квадратной матрицы А порядка n, если можно подобрать такой n-мерный нулевой вектор
Множество всех собственных значений
где λ – рассматривается в качестве независимых переменных; Е – матричная единица; det(·) – определитель матрицы.
Замечание 1. Если выполнить операцию вычисления определителя det(·) в (2), то получим выражение для характеристического полинома относительно собственных чисел:
Решение систем линейных однородных уравнений вида (1) и (2) основано на известной лемме из теории матриц [9, с. 54]: «Для того, чтобы линейная система однородных алгебраических уравнений имела нетривиальное решение, необходимо и достаточно равенство нулю ее определителя».
Пример. Найти собственные значения и собственные векторы матрицы
1) Запишем характеристическое уравнение матрицы
То есть получилось квадратное уравнение (характеристический многочлен) относительно неизвестных значений λ. 2) Решением этого квадратного уравнения будут корни:
3) Найдем собственные векторы, принадлежащие собственным значениям. Собственный вектор принадлежащий собственному значению
Верхний индекс в скобках означает принадлежность к собственному значению Поучим:
4) Проверяем условие цитированной выше леммы:
Условия выполнены, значит нетривиальное решение (3) существует. Тогда в простейшем случае системы двух уравнений [9, с. 336]:
Таким образом, ненулевой собственный вектор, принадлежащий собственному числу
Аналогично находится второй собственный вектор
Следовательно, второй собственный вектор, принадлежащий собственному числу
Замечание. Метод нахождения собственных чисел
В вычислительной математике известны различные вычислительные схемы определения собственных чисел и собственных векторов матрицы, и имеются соответствующие пакеты программ для ЭВМ. Однако до настоящего времени общепринятый стандартный простой метод решения проблемы на собственные значения и собственные векторы матриц большого размера отсутствует. Если под рукой нет подходящей программы, то можно применить один из простых приближенных методов, описанных в [1, с. 32]. В лабораторной работе применен метод под номером 4, использующий среднегеометрическую оценку компонент собственного вектора (см. ниже, пункт 1.2).
Алгоритм МАИ
Изложение алгоритма МАИ приведем, следуя [1] и [5], для наглядности совместив формальное описание с примером.
Основные положения
Метод анализа иерархий является систематической процедурой для иерархического представления компонентов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень взаимодействия элементов. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, выявления приоритетности критериев и нахождения альтернативных решений. Полученные таким образом значения являются оценками в шкале отношений и соответствуют некоторым численным оценкам. Решение проблемы – это процедура поэтапного установления приоритетов. На первом этапе выявляются наиболее важные компоненты проблемы, на втором – наилучший способ проверки наблюдений, испытания и оценка альтернатив; на следующем этапе вырабатывается решение и оценивается его качество. Процесс может быть проведен так же над последовательностью иерархий: в этом случае результаты, полученные в одной из них, используются в качестве входных данных при изучении следующей. Метод многокритериального отбора систематизирует процесс решения такой многоступенчатой задачи. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
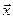 , что выполняется уравнение [10, с. 70]:
, что выполняется уравнение [10, с. 70]: или
или 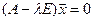 . (1)
. (1) матрицы А находится как корни характеристического или векового уравнения
матрицы А находится как корни характеристического или векового уравнения , (2)
, (2) . (3)
. (3) .
. .
. .
. , по определению является нулевым решением системы
, по определению является нулевым решением системы . (3)
. (3) , а нижний индекс – это номер простого (не кратного) корня.
, а нижний индекс – это номер простого (не кратного) корня. .
. .
.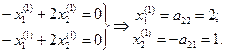
 .
. матрицы А, принадлежащий собственному значению
матрицы А, принадлежащий собственному значению  .
.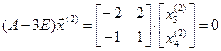 ;
; 

 .
.