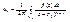|
|
Интеграл по комплексному переменному, его основные св-ва.Пусть в компл-ой пл-ти задано параметрически гладкая кривая
Мы получили конструкцию, напоминающую криволинейного интеграла для ф-ии дейст-го переменного. В предыдущих предложениях м.б получены след. вычислит. формула:
14. Теорема Коши для односвязной и многосвязной области. Опр. Односвязной областью наз. область ограниченная одним связным контуром, иначе область наз. n-связной по числу ограниченных ее связных контуров.
Т: Пусть G – односвязная область, f(z) – однозначная аналитическая ф-я, определенная на этой области и L – любая замкнутая кривая спрямляемая лежащая в G. Тогда
Оказывается, что инт. теорема Коши имеет место и длч многосвязных обл.
В случае n-связной области Т.Коши так же имеет место. Формула имеет вид: Т.Коши.: 15. Интегральная формула Коши. Т:Пусть ф-я f(z) – однозначная и аналитическая на обл.G; L- замкнутая спрямляемая, принадлежащая обл.G вместе со своей внутренней обл.Д, тогда для любой точки При этом интеграл Коши имеет вид: Замечание: интеграл Коши позволяет вычислять значение ф-ии, в некот. внутренней точки обл-ти, если известно значение ф-ии на границе этой обл-ти. Интеграл Коши (формула Коши) имеет место и для точек, лежащих вне этой области и =0. интеграл теряет смысл, для точек, кот.принадлежат границе.
16,19Бесконечная дифференцируемость аналитической функции. Ряд Тейлора. Разложение аналитической функции в Справедлива след. теорема: однозначная аналитическая в области G ф-ия f(z) разлагается в степенной ряд в окр-ти каждой точки области G. (рис.1) Р! z0 принад. G. Начертим окр-ть γρ в центре в т.z0 и радиусом ρ. Все точки на границе окр-ти будем обозначать ξ. Р! т.z внутри этой окр-ти, тогда для этой точки будет справедлива интегральная формула Коши:
Модуль дроби в знаменателе <1, т.к. Тогда по формуле бесконечно убывающей геом. прогрессии все равно:
Подставляя полученное выр-ие в интегральную формулу Коши, получим:
Почленно интегрируя данное рав-во, получим:
Т.к. полученное разложение аналитической ф-ии f(z) в степенной ряд един-о, то полученный степенной ряд будет яв-ся рядом Тейлора, коэф-ты которого выч-ся по формуле:
Р! случай, когда в некоторой отдельной изолированной точке ус-ие аналитичности нарушается. В этом случае поведение ф-и можно описать рядом Лорана:
Ряд (2) яв-ся степенным, значит область сходимости ряда – круг с радиусом R, т.е
Проинтегрируем рав-во по окр-ти γρ: Интеграл, стоящий в правой части равен 0 во всех случаях, кроме n=k. В этом случае он равен 2πi. Тогда весь интеграл равен 2πian. След-но, получается выр-ие для Формула по виду напоминает соот-ую формулу для ряда Тейлора. Формула показывает, что коэф-ты ряда Лорана выч-ся однозначно, поэтому разложение ф-ии в ряд Лорана един-но. Теорема: ф-ия f(z) однозначная и анал. в круговом кольце представима в нем рядом Лорана.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где
, где 
 ,
,  - непрерывна. На этой кривой определена непрерывная ф-ия
- непрерывна. На этой кривой определена непрерывная ф-ия 

 ,
,  - произвольным образом выбранная точка на участке.
- произвольным образом выбранная точка на участке.  . Разбиению кривой АВ на участки, соответствует разбиение отрезка от
. Разбиению кривой АВ на участки, соответствует разбиение отрезка от 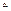 до
до 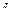 точками
точками  . Если рассмотреть предел
. Если рассмотреть предел 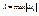 , рассмотрим предел
, рассмотрим предел  . Если этот предел
. Если этот предел 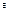 , конечен и не зависит от способа разбиения кривой АВ на участки и выбора т-ки
, конечен и не зависит от способа разбиения кривой АВ на участки и выбора т-ки  .
.  . Само определение интеграла позволяло определить интеграл вида:
. Само определение интеграла позволяло определить интеграл вида:  (*),
(*),  ,
, 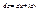 (проверить).
(проверить).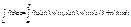 , т.е мы получили формулу:
, т.е мы получили формулу:  . По аналогии с интегралом ф-ии действ-го переменного рассмотрим св-ва: 1).Линейность
. По аналогии с интегралом ф-ии действ-го переменного рассмотрим св-ва: 1).Линейность  . 2) Аддетивность интеграла относительно области интегрирования
. 2) Аддетивность интеграла относительно области интегрирования 
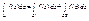 . 3) При смене направления интегрирования интеграл меняет знак
. 3) При смене направления интегрирования интеграл меняет знак  . 4) Оценка модуля
. 4) Оценка модуля  . Пример,
. Пример, 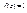

 ,
, 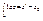 .
.


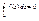 . Д-во: в дополнительном предположении, что ф-я f '(z)- непрерывна. По условию f(z) – аналитическая
. Д-во: в дополнительном предположении, что ф-я f '(z)- непрерывна. По условию f(z) – аналитическая 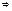 выполняется условие Коши – Римана:
выполняется условие Коши – Римана:  ;
;  , т.к. f '(z)- непрерывна, то
, т.к. f '(z)- непрерывна, то 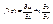
 (*) Применим ф-лу Грина:
(*) Применим ф-лу Грина: к каждому интегралу записи(*) .
к каждому интегралу записи(*) .  . Поэтому исходный интеграл
. Поэтому исходный интеграл 
 ;
;  ;
; 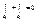
 . Получили что интеграл по границе обл. Д:
. Получили что интеграл по границе обл. Д:  .
.
 . Однако для удобства важное значение имеет интегральная
. Однако для удобства важное значение имеет интегральная Причем, контуры могут обходиться водном и том же направлении, н-р по часовой стрелки. Интеграл и первообразная. Из инт.Т.Коши
Причем, контуры могут обходиться водном и том же направлении, н-р по часовой стрелки. Интеграл и первообразная. Из инт.Т.Коши  , где F(z)-первообразная для ф-ии f(z). F’(z)=f(z). В связи с этим для функции комплексного переменного имеет место формула Ньютона – Лейбница для данной ф-ии:
, где F(z)-первообразная для ф-ии f(z). F’(z)=f(z). В связи с этим для функции комплексного переменного имеет место формула Ньютона – Лейбница для данной ф-ии:  .
. справедлива формула:
справедлива формула: 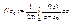 .
. 
 .
.

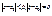
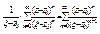

 , где
, где 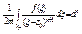 .
. . Замечание: сравнивая последнее выр-ие с последней формулой можно записать формулы Коши для зн-ий n- ой производной:
. Замечание: сравнивая последнее выр-ие с последней формулой можно записать формулы Коши для зн-ий n- ой производной: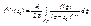 .
.
 . Ряд (1) можно преобр-ь в степенной путем замены переменной:
. Ряд (1) можно преобр-ь в степенной путем замены переменной:  . Тогда
. Тогда  . Исходный ряд будет сходиться в кольце
. Исходный ряд будет сходиться в кольце  . Рис.2. Введенная нами замена переменной не нарушает аналитичности ф-ии. Ф-ия f(z) будет бесконечно диф-ой, поэтому ряд Лорана представляет собой аналит. ф-ию в кольце. Ясно, что сходимость ряда Лорана внутри кольца будет равномерной, поэтому ряд Лорана можно почленно интегрировать по окр-ти γρ, расположенной внутри кольца: рис.3.
. Рис.2. Введенная нами замена переменной не нарушает аналитичности ф-ии. Ф-ия f(z) будет бесконечно диф-ой, поэтому ряд Лорана представляет собой аналит. ф-ию в кольце. Ясно, что сходимость ряда Лорана внутри кольца будет равномерной, поэтому ряд Лорана можно почленно интегрировать по окр-ти γρ, расположенной внутри кольца: рис.3.  .
.