
|
|
Дифференцируемость и производная функции комплексного переменного. Условия Коши-Римана. Понятие аналитической функции.Понятие функции комплексного переменного является частным случаем общего понятия функций. В этом случаи область определения и множ значений как правило являются подмнож множ С, т.е.
область множ опред. знач. z-множ т. Из обл. опред. w=f(z)
Где z-аргумент, w-функция. И этого следует, что задание функции комплексного переменного связано с заданием двух функций w=u(x,y)+i∙ v(x,y) Rew=Ref(z)=u(x,y) Imw=Imf(z)= v(x,y) Наоборот задание пары функций двух дейст. переменных можно расценивать как задание функции комплексного переменного.
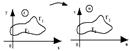
Таким образом задание функции комплексного переменного эквивалентно заданию пары функций двух действительных переменных, а геометрически оно иллюстрируется отображением множ т. z-плоскости на множ т. w-плоскости. В частности при определенных ограничениях взаимная однозначность отображ и не прерывность w=f(z) будем иметь отображение областей (это связанное открытое множ при чем граница переходит в границу) w=f(z)
1. w=z2
u(x,y)= v(x,y)=2xy 2. w= Данная функция является однозначной только в одну сторону, т.к. всем точкам w=R ставят в соответствии Говоря о функции комплексного переменного мы будем иметь в виду однозначное отображение, но случай когда одному прообразу соответствует более одного образа множ, бесконечное множ), не будет исключением в дальнейших рассуждениях. Речь тогда пойдет о многозначных функциях. 3. w=Argz – функция многозначная бесконечно-значная, т.к. 4. w= ai=const z-аргумент. Понятие производной и дифференциала ф-ии компл-го переменного. Внешне (формально) опр-е производной ф-ии в точке аналитично опр-ю производной ф-ии дйствительного аргумента.
Аналогично с ф-ей действительного переменного можно ввести понятие дифференциала.
Важное знач. имеет запись:
(*)-получили по 3 св-ву бесконечно малой ф-ии,отличается от своего предела на бесконечно малую ф-ию.
Правила дифферен-ия: 1.(CW)’=CW’, C=const 2.(f1f2)’=f1’f2+f1f2’ 3.(f1+f2)’=f1’+f2’ 4.(f1/f2)’=(f1’f2-f1f2’)/ 5.W=f(z), z=z( Необходимое и достаточное условие дифф-ти ф-ии комплексного переменного.
Т:Ф-ия f(z) диффер-ма в точке z=x+iy т.и т,к:1)ф-ии u(x;y) и v(x;y) диффер-ма в точке (x;y),как ф-ии двух действ-х переменных.2)Выполняются условия Коши-Римана:
Д-во:Ранее было 1.НЕОБХОДИМОСТЬ дано:f(z)-диффер. док-ть:1),2) док-во:по условию ф-я f(z)-дифф. значит выполняется (*)
Подставим все эти выраж-я в равенство (*) и разделим в нем действ. и мним части
Ф-ии u(х;у) и v(x;y)- это ф-ии двух действ-х переменных,условия системы гарантирует дифф. этих ф-ий в точке (х;у),т.к.
Ранее было.что
2.ДОСТАТОЧНОСТЬ дано:1),2). док-ть: f(z)-дифф-ма .Док-во: из 1ого условия
Подставить Коши-Римона Домножим второе равенство на I и сложим с первым. Учитывая равенство частных производных получим:
Сравнивая полученное с равенством (*) и обозначая ч/з
получим (**) где при достаточность доказана. Замечание: в ходе док-ва была получена формула для вычисления производной ф-ии в точке: Опр:Ф-ия W=f(z) называется аналит а т.z0 ,если она имеет производную в некотор окр-ти в этой т. z0, вкл z0/ Опр:Ф-ия W=f(z) наз-ся аналит в некотор обл,если она диффер-ма в каждой т этого множ-ва. Гармонические функции; их связь с аналитическими функциями. Восстановление аналитической функции по действительной или мнимой части. Если предположить, что ф-ии υ(x;y), иu (x;y) для аналитической ф-ии f(z)=u+iυ имеют вторые производные, то легко док-ть, что каждая из них удов-ет так называемому ур-ию Лапласа:
Ф-ия двух дейст. переменных наз-ся гармонической в области G, если она обладает непрерывными частными производными 2-го порядка и удов-ет ур-ию Лапласа. Т.о. верно утверждение: дейст. и мнимая части аналитической ф-ии в области G яв-чя гармоническими в G. Пример: восстановить аналитическую ф-ию w=f(z) по ус-ям: u(x;y)=x4-6x2y2+y4, f(0)=0. Для начала нужно проверить яв-ся ли ф-ия гармонической, т.е. удов-ет ли ус-м Лапласа:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
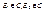 .
.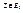
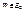
 ,
, 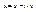
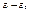
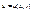 , v=v(x,y)
, v=v(x,y)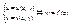
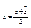
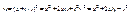

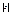

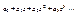
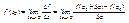

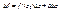 (*)
(*)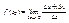
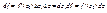 -дифференци-ая ф-ия.
-дифференци-ая ф-ия.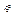
 ), W’=(dW/dz)(dz/d
), W’=(dW/dz)(dz/d 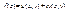
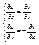
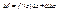 (*)
(*)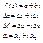
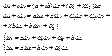
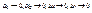
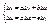

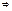
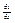 ∆
∆ 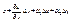
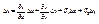
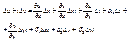
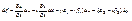
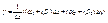
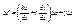 (**)
(**)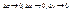 и
и 
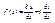
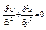 .
.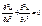 .
.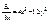 ,
, 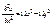
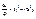 ,
,  .
.