
|
|
Дробно - линейная функция и её свойства.
Для того чтобы было комфорными, нужно чтобы Интересен случай когда
Ф-ия будет аналитической, поэтому она отобр. конформным отображением Для рассмотрения св-в этой функции рассм. частный случай Этот частный случай получается из общего Св-ва этой функции состоит в том, что это преобр. явл. композицией 2-ч преобразов. симметрии. 1. Инверсия – преобр. точки относительно окружности (0,1). 2. Симметрии относительно прямой (в данном случае отн. оси ОХ).
Любое дробно-линейное отображение
Можно описать как композицию 2-х преобразований: подобие и симметрии Кроме этих св-в дробно-линейн функции обладает след св-ми. 1. Групповое. Совокупность всех дробно-линейных преобразований образует группу относит. операции умножения.
2. Круговое Можно обосновать что при дробно-линейном отображение любая окружность отображения в окружность в частности прямую можно рассмотреть как частн. случай окружности с бесконечн радиусом. На практике выяснить в какую линию преобразовать исходн. линию позволяет подстановка(проверка) принадлежности праобразу точки
3. Дробно-линейная функция может быть обнозначно задана с помощью указания образов 3-х точек.
В результате получим
Замечание: Если окажется, что какое-то из чисел
4. С помощью дробно-линейного отображения можно совершать преобразования круговых областей, руководствуясь правилом обхода области по контуру. Например при обходе по границе области праобраза от т.
Cтепенная функция и радикал. Понятие о Римановой поверхности. Общий вид степенной функции с натуральным показателем Рассмотрим теорию для частного случая, который получается из общего параллельным переносом на вектора
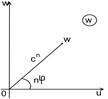
Для частного случая Рассмотрим св-ва: Определим, как будет отображаться координатная сетка. Зафиксируем для этого z.
Рассмотрим угол
При том образом данного угла будет вся w плоскость с разрезом по положительным направлениям оси Ox
Если угол
То образ начнет покрывать W-плоскость вторично, как бы переходя на новый лист W-плоскости как по винтовой линии. Когда Увеличивая При В трехмерном пространстве такие поверхности не помещаются, след-но они пред-ют собой идеальную модель. В z=0 конформность отображения нарушается, поэтому соотв-ю ей точку N=0, называют точкой разветвления n-го порядка. Рассм ф-цию обратную к степенной
Если рассм ф-цию
Показательная функция. Показательная ф-ция
Рассмотрим св-ва показ-й ф-ции: 1. 2.
3.
4. Периодичность ф-ции
Рассмотрим св-ва отображения z-плоскости с помощью этой ф-ции
1) x=с=const 2) y=с Логарифмическая функция.
Пример: Ln(-i)=? Z=-i
Логарифмическая функция – бесконечнозначная функция. Можно показать, что справедливы все формулы для логарифма, аналогичные соответствующим ф-лам для действит-го логарифма.
Иногда бывает полезно рассмотреть главные значения логарифма: Рассмотрим рассуждения о вышесказанных показат-х функциях следует, что отображение взаимнооднозначное для полосы
При отображении соседних полос будут получаться следующие экземпляры w-плоскости с разрезом, поэтому логарифмическая ф-ция будет однозначной на своей бесконечно-листной римановой пов-ти. При чем

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
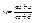

 , т.к. функция превращается в линейную.
, т.к. функция превращается в линейную.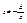
 - плоскости, т.е.
- плоскости, т.е. 
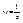 .
. .
.


 , если
, если




 , то с использованием понятия линейн. перехода можно доказать, что в этом случае для нахождеия дробно-линейн. ф-ии, разность в котор входит бесконечность нужно заменить на 1.
, то с использованием понятия линейн. перехода можно доказать, что в этом случае для нахождеия дробно-линейн. ф-ии, разность в котор входит бесконечность нужно заменить на 1.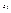 до т.
до т.  область остается справа, то и при обходе обл. образа т.
область остается справа, то и при обходе обл. образа т.  до
до  область будет так же оставаться справа.
область будет так же оставаться справа.






 , поэтому отображение будет конформным.
, поэтому отображение будет конформным.




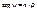




 будет расти и примет значение
будет расти и примет значение 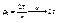

 , то W покроется вторично.
, то W покроется вторично. , мы получим образ, соответствующий
, мы получим образ, соответствующий  , т.е. последний n-ый лист римановой поверхности должен без самопересечения склеиться с первым листом.
, т.е. последний n-ый лист римановой поверхности должен без самопересечения склеиться с первым листом.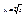 , z – натур. Эта ф-ция в кажд точке z ставит в соотв-ии
, z – натур. Эта ф-ция в кажд точке z ставит в соотв-ии 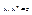 , кот-я м.б. вычислена по ф-ле Муавра.
, кот-я м.б. вычислена по ф-ле Муавра. Эта ф-ла при
Эта ф-ла при 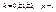 , позволяет получить n-разных знач-й корня n-й степени.
, позволяет получить n-разных знач-й корня n-й степени. все значения этого корня лежат на окружности с центром (0;0) и
все значения этого корня лежат на окружности с центром (0;0) и  и являются вершинами правильного треугольника (n-угольника n=3)
и являются вершинами правильного треугольника (n-угольника n=3) м.б. определена с помощью ряда
м.б. определена с помощью ряда
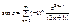


 отображение конформно в любой точке пл-ти.
отображение конформно в любой точке пл-ти.




 , k=0,1,…
, k=0,1,…



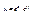 ,
, 


 Логарифм ф-ция каждому
Логарифм ф-ция каждому 








 , k=0,1,2,…
, k=0,1,2,…





 и т.д.
и т.д.

