
|
|
Определения и основные свойства.Определение 1: Бинарное отношение r между множествами A и B(rÌA´B) называется функцией, если arbÙarc Þ b= c. То есть если "xÎA существует не более одного элемента yÎB такого, что xry. Если xry, то нам удобно будет записывать y=r(x), при этом первый элемент пары (x, y) будем называть аргументом, а второй- значением функции на элементе x, или просто функция от x . Функции обычно обозначаются строчными буквами латинского алфавита f, g, h, ... или специальными наборами символов, таких как sin, log, ... Говорят, что функция f действует из A в B и записывают это так: f:A®B, если при этом x f y, то есть y=f(x), то говорят, что функция f отображает элемент x в y и записывают так: f: x ay. Или говорят, что y есть образ элемента x при отображении f, а x есть прообраз y. Последнее обозначение удобно, когда следует явно указать закон, по которому действует функция. Пример 1: f: A®A, где A={-1; 0; 1} по правилу f: x ax3. Пример 2: Это пример того, что не всякое отношение является функцией
а) f - не является функцией б) g - является функцией Поскольку всякая функция, действующая из A в B, является отношением на множествах A и B, то можно дать следующее определение: Определение 2: Областью определения функцииf: A®B называется область определения отношения fÌA´B, то есть Df={xÎA| $yÎB ((x,y)Îf)}={xÎA| $yÎB (x f y)}={ xÎA| $yÎB (y=f(x))}, то есть DfÍA. Определение 3: Областью значений функцииf: A®B называется область значений отношения fÌA´B, то есть Ef={yÎB| $xÎA ((x, y) Îf)}= {yÎB| $xÎA (x f y)}= {yÎB| $xÎA ( y=f(x))}, то есть EfÍB. Определение 4: Две функции f: A®B и g: A®B называют равными и пишут f=g тогда и только тогда, когда они равны как подмножества прямого произведения A´B, то есть если (x, y)Îf Û(x, y)Îg. Замечание: Ясно, что если f=g, то Df=Dg и Ef=Eg. Вопрос: Верно ли обратное утверждение? Если нет, то приведите пример. Определение 5: Функция f: A®B называется отображением, если ее область определения совпадает с A (Df=A). При этом говорят, что f отображает множество A в (или на) множество B. Примеры: 3. sin: R®R , отображение множества R в R 4. ln: R®R – функция, действующая из R в R. Dln={xÎR| x>0}=R+. ln: R+®R – здесь уже является отображением множества R+ на все R. Определение 6: Функция f: A®R называется функцией, принимающей действительные значения. Функцию f: R®R называют действительной (вещественной) функцией. Определение 7: Если f: A®B и A есть прямое произведение множеств A1´A2´...´An, то говорят, что f естьфункцияn переменных. Тогда вместо f((x1, x2,..., xn))пишут f(x1, x2,..., xn). В частности: f(x, y) - функция двух переменных, f(x, y, z) - функция трех переменных. Примеры: 5. f: R´R®R. f(x, y) a x+y, то есть (x, y, x+y)ÎfÌR3. В этом случае можно писать z=x+y. 6. f: N´N ® Q. f(x, y) a x/y, можно записать z=x/y В математике часто используются функции и отображения, которые обладают некоторыми очень важными свойствами. Определение 8: Функция f: A®B называется сюръективной («на», то есть действует из A на B) если Ef=B. Или: Другими словами: у каждого элемента из B есть прообраз в A. Определение 9: Функция f: A®B называется инъективной, если Условие инъективности можно записать следующим образом: "x,yÎDf(x¹yÞf(x)¹f(y))(почему?) Определение 10: Функция f: A®B называется биективной, если она инъективна и сюръективна .Если Df=A, то говорят, что f - биекция или взаимно-однозначное отображение множества A на множество B. Примеры: 7. отображение из примера 2 б) сюръективно, но не инъективно 8. sin: R®[-1;1] сюръективно, но не инъективно, а вот sin: [-p/2;p/2]®[-1;1] – биекция 9. exp:R ®R. exp: x a ex инъективно, но не сюръективно 10. f: N ®{натуральные, четные}; f: n a 2n - биекция
Композиция функций Под композицией функций f и g будем понимать композицию отношений f и g и обозначать fog или gof. Ясно, что о композиции функций fog имеет смысл говорить, если Теорема 1 (о композиции): Пусть g: A®B и f: B®C - функции. Тогда их композиция fog тоже является функцией, причем 1. D fog={xÎA| g(x)ÎDf} 2. (fog)(x)=f(g(x)) для каждого xÎD fog 3. fog={(x, f(g(x))|"x (g(x) ÎDf} Доказательство: По определению композиции отношений имеем: fog={(x, y)| $zÎB ((x,z)ÎgÙ(z,y)Îf)}. Так как g - функция, то для каждого x существует единственный zÎB, а так как f - функция, ему не может соответствовать более одного y из C, поэтому если (x, y) Î fog и (x, y1) Î fog, то y=y1, так как z - один и тот же. Далее, из этого же равенства, если (x, y) Îg, то xÎDg и z=g(x) (1), а если (x,y) Îf и f - функция, то z=g(x)ÎDf (2) и y=f(z)=f(g(x)) (3). Чтобы композиция была определена (z существовал) необходимо и достаточно, чтобы g(x) ÎDf , но это и означает, что Dfog={xÎA| g(x) ÎDf} , свойства 2) и 3) автоматически следуют из равенств (2) и (3). Что и требовалось доказать. Упражнение 1: Пусть f: A®B и g: B®C - функции. Что является областью определения функции gof, если: a) f - функция, g - отображение b) f - отображение, g - функция c) f и g – отображения? Вернемся к свойствам композиции. Теорема 2: Пусть f: A®B и g: B®C - функции. Тогда: a) если f и g инъективны, то gof инъективна b) если f и g сюръективны, то gof сюръективна c) если f и g биективны, то gof биективна. Доказательство: a) Пусть x1, x2ÎDgof и x1¹x2. Пусть y1=(gof)(x1), а y2= (gof)(x2), но по теореме 1 y1=g(f(x1)) и y2=g(f(x2)). Но f(x1)¹f(x2), в силу инъективности f, а значит g(f(x1))¹ g(f(x2)) в силу инъективности g. b) самостоятельно c) следует из а) и б) Что и требовалось доказать. Замечание: Если f и g вещественные функции, то gof или fog называют сложной функцией. Пример 11: f:R®R, x a sin x, g:R®R, g: x a Свойство 1(композиции): (fo g)o h= fo (go h). Доказательство следует из соответствующего свойства отношений.
Обратные отображения. Пусть f: A ® B – функция. Нам следует ответить на вопрос: когда отношение f -1 будет функцией? Вспомним пример 2б) из §1. Там g – отображение, а вот отношение g -1 не является таковым, поскольку g={(c, a); (c, b)}. Прежде чем переходить к более подробному обсуждению, введем некоторые понятия, которые понадобятся нам в дальнейшем. Определение 1: f: A®B, при этом y=f(x). Тогда множество f–1(y)={x|f(x)=y}ÍA называется полным прообразом элементаy. Пусть CÌA. Множество f(C)={y|xÎCÙy=f(x)}ÍB называется образом множества C. Если DÌB, множество f–1(D)={x|f(x)ÎD}ÍA называется полным прообразом множества D. Теорема (основное свойство биекции): Если f - биективное отображение множества X на множество Y и A и B подмножества X, то f(AÇB)=f(A)Ç f(B). (образ пересечения равен пересечению образов). Доказательство: Пусть yÎf(AÇB) Þ $xÎAÇB, такое что y=f(x) Þ xÎA Ù xÎB Þ f(x)Îf(A) Ù f(x)Îf(B) Þ f(x)=y Î f(A)Çf(B). Обратно, пусть yÎ f(A)Çf(B) Þ yÎf(A) Ù yÎf(B), тогда, поскольку f – биекция, значит, у y есть единственный прообраз - x, причем xÎA Ù xÎB Þ xÎAÇB Þ f(x)=yÎf(AÇB). Что и требовалось доказать. Замечание 1: Требование биективности можно ослабить и заменить инъективностью (докажите). Замечание 2: Для произвольной функции выполняется лишь f(AÇB)Ìf(A)Çf(B). (докажите и приведите пример, когда обратное включение не имеет места) Определение 2: тождественнымотображением множества X на себя называется тождественное отношение на X, то есть IX: X®X по правилу IX: x a x. Теперь мы готовы приступить к ответу на поставленный в начале параграфа вопрос. Ответ на него дает критерий: Теорема (критерий инъективности): функция f: A® B инъективна тогда и только тогда, когда f -1: B® A является функцией. Доказательство: Отношение f -1 является функцией тогда и только тогда, когда (z, x)Îf -1Ù(z, y)Î f –1 Þ x=y º (x, z)Îf Ù (y, z)Îf Þ x=y º z=f(x) Ù z=f(y) Þ x=y º (в силу транзитивности равенства и того, что x, y ÎDf) f(x)=f(y) Þ x=y. Но это и есть требование инъективности. Что и требовалось доказать. Следствие 1: если f инъективна, то f-1 тоже инъективна. (самостоятельно) Следствие 2: если f биективное отображение A на B, то f -1 тоже биективное отображение B на A. Пусть функция f: A®B инъективна и aÎDf, тогда f(a) ÎEf. Ясно, что f–1(f(a))=a, так как если бы полный прообраз элемента f(a) состоял не из одного элемента, то это противоречило бы инъективности f. С другой стороны, если bÎEf, то, поскольку Ef= Теорема: если функция f инъективна, то f -1o f = Следствие 1: если f биекция A на B, то f -1o f = IA и fo f –1= IB.. Замечание: это утверждение можно обратить. Определение 3: биективное отображение множества A на себя называется преобразованием множества A. Следствие 2: если f есть преобразование множества A , то f -1o f = fo f –1= =IA.. Далее. Если функции f: A®B и g: B ®C инъективны, то gof - тоже инъективна и значит определена (gof)-1, которая, по соответствующему свойству отношений, равна f –1 o g -1 и действует из C в A. Оформим этот факт в виде утверждения: Свойство 2 (композиции функций): если f и g инъективны и gof функция, то (gof)-1= f –1 o g -1. Следствие: если f: A®B и g: B ®C биективные отображения, то (gof)-1 есть биекция C на A, при этом (gof)-1= f –1 o g -1.
§4. Мощность множества. Мы уже говорили раньше о мощности некоторых множеств и даже ввели понятие конечного и бесконечного множеств. Теперь, вооружившись понятием биекции, мы можем это сделать более строго. Определение 1: два множества называются биективными(обозначается X~Y), если существует биективное отображение X на Y. Замечание. Очевидно, что отношение «быть биективными» («~») на множестве всех множеств является отношением эквивалентности (проверьте!). Поэтому во многих книгах по теории множеств вместо слова «биективные» используют слово - «эквивалентные» Введем обозначение Nm={1, 2, 3, ..., m}, где mÎN. При этом, не вдаваясь в подробности, мы будем пользоваться тем, интуитивно ясным фактом, что Nm не биективно Nk, если m ¹ k Определение 2. Два множества имеют одинаковую мощность (равномощны), если они биективны и будем писать |A|=|B|. При этом будем считать, что /Æ/=0, так как оно биективно только самому себе. Множество X называется конечным, если $ mÎN (Nm~X), при этом говорят, что мощность X равна m, /X/=m . Множество называется счетным, еслиN~X , обозначается | X| = À0 . Множество X имеет мощность континуум, если оно биективно отрезку [0, 1] Ì R,обозначение: |X| = À1. Обсудим сначала свойства конечных и счетных множеств. Установить биекцию между множеством X и Nm (или N) - это значит каждому элементу из X поставить в соответствие единственное натуральное число, начиная с 1, то есть попросту пронумеровать. Таким образом, если X ~ Nm, то его можно расположить в виде конечной последовательности x1, x2,..., xm. А если X ~ N, то в виде бесконечной последовательности x1, x2, .... Поэтому, чтобы построить биективное отображение Nmна X или Nна X, достаточно указать алгоритм перенумерования элементов множества X. Обсудим некоторые свойства конечных множеств. Свойство 1. Если S конечно и f: S ® S инъективное отображение, то f - биекция. Доказательство. Если S = Æ, то результат тривиален. Пусть S ¹ Æ. Тогда существует биекция Nm~ S для некоторого m Î Nи S можно записать в виде S= {а1, а2, ..., аm }, тогда f(S) ={ f(a1), f(a2), ..., f(am) }, причем все f(ai)- различны, т.к. f- инъективно. Пусть f(S) ¹ S, т. е. есть элементы b1, b2, ..., bk которые не принадлежат f(S). Тогда S= { f(a1), f(a2),..., f(am), b1, b2,..., bk }. Тогда рассмотрим отображения Nm+k ® S : 1® f(a1), ..., m® f(am), m+1 ® b1, ..., m+k ® bk . Это биекция. Значит S ~ Nm+k. Противоречие. Что и требовалось доказать. Следствие: Множество N - бесконечно ( не является конечным). Доказательство: Отображение f: N ® N ,по правилу n a n+1 инъективно, но не сюръективно ( у 1 нет прообраза). Значит N не является конечным.В качестве пояснения можно предложить следующую цепочку логически эквивалентных формул: ( A Ù B Þ C º Что и требовалось доказать. Это значит, что N не биективно никакому своему конечному подмножеству. Определение 2. Символ, соответствующий мощности некоторого множества, называется кардинальным (порядковым) числом. В частности, к кардинальным числам относятся все натуральные числа, а также À0 и À1. Определение 3: Кардинальное число, не являющееся натуральным, называется трансфинитным числом. Оказывается, что множество всех кардинальных чисел можно упорядочить, т. е. построить на этом множестве отношение полного порядка. Прежде чем переходить к построению этого порядка продолжим изучение свойств конечных и счетных множеств. Определение 4. Подмножество A из R ограничено сверху (снизу), если в R существует наибольший (наименьший) элемент для множества А. Множество А называется ограниченным, если оно ограниченно сверху и снизу. Свойство 2. Ограниченное подмножество из N - конечно. Доказательство: Поскольку N Ì R , то каждое подмножество из N ограничено снизу нулем. Пусть АÌ N ограничено сверху некоторым m Î N. Рассмотрим отображение f: A ® N, такое что если А= {a1, a2,..., ai,...} и а1 < а2 < а3 <... < m, то f(ai) = i. Ясно, что f(ai) £ ai и ясно также , что f- инъективно. Должно существовать n £ m, такое что f: A® Nn - биективно. Если это не так, то $ ар Î А (f(ap) > m), а значит ap ³ f(ap) > m. Но А ограничено сверху числом m. Противоречие. Значит, А - конечно. Свойство 3. Каждое подмножество конечного множества - конечно. Доказательство: Пусть А Í В и В - конечно. Если В= Æ, то А=Æ и утверждение доказано. Пусть В ¹ Æ. Тогда существует биекция f: В ~ Nm, для некоторого m Î N. Тогда f(A) Í Nm, следовательно, f(A) ограничено, а значит, конечно. Но f(A) ~ A, значит А тоже конечно. Что и требовалось доказать. Следствие. Любое множество, имеющее бесконечное подмножество, само бесконечно. Перейдем теперь к счетным множествам (см.[11], [12]). Утверждение 1. Множество всех целых чисел счетно (|Z| = À0). Доказательство: Построим биекцию N ® Z следующим образом: 0 «1, -1 « 2, 1 « 3, -2 « 4, 2 « 5. Т.е. n « 2n + 1, если n ³ 0 n « 2|n| , если n < 0. Что и требовалось доказать. Упражнения: 1. Доказать, что множество всех четных положительных чисел счетно. 2. Доказать, что множество 2, 4, 8, ..., 2n - счетно. Утверждение 2: Множество всех рациональных чисел счетно. (|Q|= À0). Доказательство: Каждое рациональное число однозначно записывается в виде несократимой дроби Что и требовалось доказать. Установим теперь некоторые общие свойства счетных множеств. Свойство 1. Всякое подмножество счетного множества конечно или счетно. Доказательство: Пусть А- счетное множество, а В- его подмножество. Занумеруем элементы множества А= {а1, а2, ..., аn, ...}. Пусть an1, an2, ... те из них, которые входят в множество В. Если среди чисел n1, n2, ... есть наибольшее, то В- конечно. В противном случае В- счетно, т.к. его элементы an1, an2,... занумерованы числами 1, 2,... Что и требовалось доказать. Свойство 2: Объединение любого конечного или счетного множества счетных множеств есть счетное множество. Доказательство: Пусть А1, А2,... - счетные множества. Мы можем считать, что они попарно не пересекаются, т.к. иначе мы рассмотрели бы вместо них множества А1, А2 \ А1, А3\ (А1 È А2 ), ... , каждое из которых не более чем счетно по свойству 1, а их объединение равно А1È А2È.... . Поскольку каждое из множеств А1, А2,... счетно, то все элементы множества А1, А2, ... можно записать в виде следующей бесконечной таблицы: Занумеруем все элементы по диагоналям (как показано на рисунке).
Ясно, что при этом каждый элемент каждого из множеств получит определенный номер. Т.о. будет установлено взаимно- однозначное соответствие между А1È А2 È... и множества N. Что и требовалось доказать. Свойство 3. Всякое бесконечное множество содержит счетное подмножество. Доказательство: Очевидно. Доказать самостоятельно (указание: выбираем, нумеруем, нехватки элементов не будет, поскольку множество бесконечно). Теперь мы готовы к тому, чтобы ввести отношение порядка на множестве кардинальных чисел. Для мощностей конечных множеств это сделать несложно, поскольку (см.[4]) ½Nk½£ | Nm |, если k £ m. Но как быть с бесконечными множествами? Основой для упорядочивания служит теорема Кантора- Бернштейна: Теорема ( Кантор- Бернштейн). Пусть А и В два произвольных множества. Если множество А биективно некоторому подмножеству множества В, а В биективно некоторому подмножеству множества А, то множества А и В биективны. ( Без доказательства, см.[11]) С учетом этой теоремы для двух произвольных множеств А и В логически возможны следующие случаи: 1) А биективно некоторому подмножеству В, а В биективно некоторому подмножеству А. 2) А содержит подмножество, биективное В, но в В нет подмножества биективного А. 3) В содержит подмножество, биективное А, но в А нет подмножества биективного В. 4) Ни в одном из этих двух множеств нет подмножества биективного другому. В первом случае множества А и В в силу теоремы Кантора- Бернштейна биективны, а значит | А | = | В |. Во втором случае естественно считать, что | В | < | А |, а в третьем | А | < | В |. Наконец, в четвертом случае нам пришлось бы считать, что мощности множеств А и В несравнимы между собой. На самом деле этот случай невозможен ! (см. [11]). Итак, для любых двух множеств А и В можно сказать, что либо | А | = | В |, либо | А | < | В |, либо | В | < | А |. Таким образом, учитывая свойство 1 счетных множеств и следствие из свойства 1 конечных множеств, можно сказать, что "k Î N ( k < À0). Более того, учитывая свойство 3 счетных множеств, можно сказать, что счетное множество есть самое «маленькое» из бесконечных множеств. А что можно сказать про À0и À1- ? Утверждение 3: À0 < | [0, 1] | = À1. Доказательство: Пусть | [ 0, 1] | = À0, т.е. все элементы множества [ 0, 1] можно перенумеровать. Пусть a1= 0, а11 а12 а13... а1n... a2= 0, а21 а22 а23... а2n... a3= 0, а31 а32 а33... а3n... (1) ..................................... an= 0, аn1 an2 an3... ann... ..................................... здесь aik- k-я десятичная цифра числа ai. Построим число b= 0, b1b2b3...bn..., применив так называемую диагональную процедуру Кантора: пусть b1- любая цифра не совпадающая с а11, b2- любая цифрв не совпадающая с а22 и т.д., bn- произвольная цифра, не совпадающая с аnn. Эта дробь не может совпадать ни с одной дробью из списка (1), поскольку b отлична от a1, по крайней мере первой цифрой, от a2- второй, от an- n- ой. Таким образом, никакое счетное множество действительных чисел, лежащих на отрезке [0, 1] не исчерпывает этого множества. Значит À0 < À1. Что и требовалось доказать. Замечание 1. Некоторые числа могут быть записаны в виде десятичной дроби двумя способами: с бесконечным числом нулей или с бесконечным числом девяток. Таким образом, несовпадение двух десятичных дробей еще не гарантирует различия изображаемых ими чисел ( Упражнение: Доказать, что существует биекция между 1). [0, 1] и (0, 1), 2). [0, 1] и [0, 1), 3). [0, 1] и (0, 1 ]. Утверждение 4: | [a, b ]| = |[c, d ] | , если a< b и c< d. Доказательство: Надо установить биекцию: [a, b] ~ [c, d]. Ее легко построить, рассмотрев рисунок:
Для построения требуемой биекции достаточно выписать уравнение прямой, проходящей через точки А (а, с) и В (b, d). Что и требовалось доказать. Таким образом (с учетом результатов упражнения 4) получаем, что все отрезки, интервалы и полуинтервалы - равномощны (они имеют мощность континуум). Утверждение 5: | R | = À1. Доказательство: В силу утверждения 4 (0, 1) ~ (- tg: (- Можно доказать, что если есть множество некоторой мощности, то всегда можно построить множество большей мощности. В частности, если А - некоторое множество, то его мощность | А | < | Р(А) |. Известно (см. [12]), что | Р(N) | = À1, а мощность множества всех непрерывных на [0. 1] функций больше À1. Естественно, что |Р(R)|, больше À1. Однако |R´R| и |R´R´R| равны À1. ( Доказательство и подробное обсуждение есть в книгах [11] и [12]). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

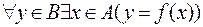 .
. .
. . Однако, возникает вопрос: если даже отношение fog определено, то будет ли оно функцией? И какими свойствами обладает композиция двух функций? Ответ на первый вопрос дает теорема:
. Однако, возникает вопрос: если даже отношение fog определено, то будет ли оно функцией? И какими свойствами обладает композиция двух функций? Ответ на первый вопрос дает теорема: , тогда fog : x asin
, тогда fog : x asin  , gof : x a
, gof : x a  . Найдите Dgof и Dfog.
. Найдите Dgof и Dfog. , bÎ
, bÎ  и fo f –1=
и fo f –1=  .
. º
º  º (
º (  )
)  º
º  º B
º B  ).
). =
=  , q Î N, p Î Z. Назовем сумму | p |+ q высотой рационального числа a. Ясно, что число дробей с данной высотой n- конечно. Например, высоту 1 имеет только одно число
, q Î N, p Î Z. Назовем сумму | p |+ q высотой рационального числа a. Ясно, что число дробей с данной высотой n- конечно. Например, высоту 1 имеет только одно число  = 0; высоту 2 числа
= 0; высоту 2 числа  и
и  ; высоту 3 числа
; высоту 3 числа  ;
;  ;
;  ;
;  . Будем нумеровать все рациональные числа по возрастанию высоты. Т.е. сначала выпишем числа высоты 1, потом- числа высоты 2 и т.д. При этом всякое рациональное число получит некоторый номер, т.е. будет установлено взаимно- однозначное соответствие между N и Q.
. Будем нумеровать все рациональные числа по возрастанию высоты. Т.е. сначала выпишем числа высоты 1, потом- числа высоты 2 и т.д. При этом всякое рациональное число получит некоторый номер, т.е. будет установлено взаимно- однозначное соответствие между N и Q.

 ;
;