Бинарная операция – модуль.

Пусть даны два действительных числа m и n. Частным от деления n на m называется величина – , а остатком от деления n на m называется выражение «n mod m». Тогда для любых действительных чисел n и m:

n = m + n mod m.

Определение. Для произвольных действительных чисел x и y определим бинарную операцию – модуль y:

x mod y = x – y , если y ≠ 0. (11.1)

(Модулем называют число, которое стоит после « mod »)

Пример 1: 7 mod 4 = 7 – 4 = 3,

7 mod - 4 = 7 – (– 4) = – 1,

– 7 mod 4 = – 7 – 4 = 1,

– 6 mod – 4 = – 6 – (– 4) = – 2.

В случае когда x и y – вещественные положительные числа, смысл

x mod y легко уловить интуитивно.

Например, представим себе секундную стрелку часов, которая движется по кругу с длиной окружности 60, точкам которой приписаны вещественные числа из интервала [0, 60). Когда стрелка пробежит расстояние х по окружности, она остановится в точке x mod 60 . А пока стрелка движется по кругу, точка 0 встретится на ее пути раз.

В случае когда x и y – вещественные отрицательные числа, нужно внимательно осмыслить определение, чтобы выяснить, что представляет собой x mod y. Разберем случай, когда y < 0:

7 mod - 4=7 – (– 4) = –1.

Величина = = – 2, т.к. пол числа х – есть наибольшее целое, меньшее или равное х.

Из рассмотренных примеров и определения функции пол можно заключить, что величина x mod y лежит между нулем и модулем:

0 ≤x mod y < y при y > 0

0 ≥ x mod y > y при y < 0.

В случае если y = 0, то x mod 0 = x. Это значит, что x mod y отличается от х на величину кратную у. Иными словами x mod 0 = x

тогда и только тогда, когда х кратно у. Подобное соглашение сохраняет свойство x mod y всегда отличаться от х на величину, кратную у.

Как говорилось выше, любое действительное число можно представить в виду суммы его целой и дробной частей: х = + {x}. Дробная часть числа может быть представлена как x mod 1, потому что

х = + x mod 1.

Пример 2: Пусть х = 2,5. Тогда 2,5 = + 2,5 mod 1. Найдем целую и дробную части числа 2,5:

= 2;

2,5 mod 1 = 2,5 – 1· = 2,5 – 1 · 2 = 0,5.

Итак, 2,5 = 2 + 0,5.

Свойство 1: Операция mod подчиняется распределительному закону:

с(х mod y) = (сх) mod (сy), где с, х, у Î R .

∆Действительно,

с(х mod y) = с(x – y ) = сх – су = (сх) mod (сy) = сх mod сy.

В примере 1 иллюстрируется этот закон для случая с = – 1. ▲

Свойство 2: Если для любых действительных чисел х , у и целого числа z

х mod z = y mod z, то х – у — целое число, кратное z.

∆ Доказательство. Для доказательства используем определение операции модуль: x mod z = x – z ; y mod z = y – z .

Тогда, x = x mod z + z ; y = y mod z + z . Составим разность: x – y = x mod z + z – y mod z – z .

Т. к. по условию х mod z = y mod z, то

x – y = z – z = z ( – ).

Разность полов, стоящая в скобках есть целое число, а, следовательно, и вся правая часть есть целое число, кратное z. ▲

Определение. Если два целых числа х и у удовлетворяют условия:

х mod z = y mod z, то говорят, что «х сравнимо с у по модулю z» и записывают: х ≡ у (по модулю z).

Исходя из вышедоказанного свойства, можно сказать, что х и у сравнимы по модулю z, если z делит разность х – у: х ≡ у (по модулю z).

Определение. Два целых числа х и у называются взаимно простыми, если их наибольший общий делитель равен 1, т.е. числа х и у не имеют общих множителей. Символически записывают: х ^ у .

Свойства сложения, вычитания и умножения по модулю аналогичны обычным операциям сложения, вычитания и умножения.

Свойство 3: Если s ≡ t (mod z) и х ≡ у (mod z), то справедливы следующие утверждения: a) s + x ≡ t + y (mod z); b) s – x ≡ t – y (mod z) и

c) s x ≡ t y (mod z).

∆ Доказательство. Рассмотрим сначала равенства а) и b). Из определения сравнимости чисел s, t и x , y можем записать: z/(s – t) и z/(x – y). Следовательно, z/(s – t) ± z/(x – y), откуда сделав некоторые преобразования, получим: z/(s + x) – z/(t + y) и z/(s – x) – z/(t – y), что по определению соответствует утверждениям а) и b).

Рассмотрим теперь равенство с). Из свойства 2 следует, что разности

s – t и x – y принадлежат множеству целых чисел и кратны числу z, т.е.

s – t Î z Z ; x – yÎz Z. Тогда sx – ty = (sx – tx) + (tx – ty)=( s – t)x–t(x – y) Î zZ, т.е. s x = t y (mod z). ▲

Свойство 4: Если числа kх и kу сравнимы по модулю z, где k их общий множитель — kх ≡ kу (mod z), то обе части сравнения можно разделить на число k, взаимно простое с z.

Доказательство. Из определения kх ≡ kу (mod z) следует, что z делит разность kx – ky, т.е. z / k(x – y). Числа z и k взаимно простые по условию, следовательно, z делит разность (x – y). Тогда по определению числа x и y сравнимы по модулю z: х ≡ у (mod z). ▲

Свойство 5: Если в сравнении kх ≡ kу (mod kz), (где k ≠ 0) x, y и модуль z имеют общий множитель k, то каждое из этих чисел можно разделить на k.

Доказательство. Для доказательства воспользуемся определением модуля. Т.К. kх ≡ kу (mod kz), то kz / k(x – y), следовательно, z / (x – y), а это значит х ≡ у (mod z). ▲

Свойство 6: Если числа s и t взаимно простые, т.е. s ^ t, то x сравнимо с y по модулю st х ≡ у (mod st) тогда и только тогда, когда

х ≡ у (mod s) и х ≡ у (mod t)

Доказательств. Пусть х ≡ у (mod s) и х ≡ у (mod t), то можем записать: s / (x – y) и t / (x – y), причем x и y – произвольные целые числа,

x ≠ y. Тогда разность x – y делится на s и на t, где числа s и t взаимно простые, s ^ t. Тогда x – y делится на st.

Обратное, если х ≡ у (mod st), то s t / (x – y).

Следовательно, s / (x – y) и t / (x – y), т.е. х ≡ у (mod s) и х ≡ у (mod t), для любых х и у.

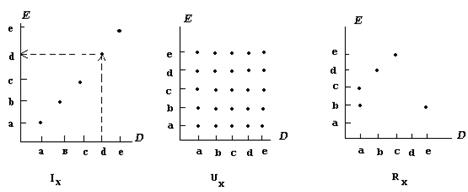
ГЛАВА III

Отношения

В этой главе мы рассмотрим понятия отношения между элементами данного множества и между элементами нескольких множеств. Это интуитивно ясное понятие (например, элементы двух множеств находятся в некотором отношении, если они удовлетворяют некоторым требованиям) является довольно общим. Поэтому оно широко применимо. Приведем несколько описательных примеров.

Два элемента из множества всех людей могут находиться в отношении «быть родственниками»; два слова из словаря могут находиться в отношении «порядка следования по алфавиту»; элементы из множества всех треугольников могут находиться в отношении «иметь равную площадь»; два элемента из множества N могут находиться в отношении «быть делителем» и т.п.

Прежде чем подойти к этому вопросу с математической позиции, рассмотрим несколько идей, возникающих из рассмотрения следующей простой ситуации. Предположим, что для некоторой машины мы имеем конечное множество программ Р, конечное множество значений данных Д и множество результатов R. Каждый элемент из Д может использоваться в некоторых программах из Р и каждый элемент из Р может использовать некоторые данные из Д. Если d_Д и р_Р, то d и р могут находиться в отношении «возможность использования» . Поэтому имеет смысл рассматривать пары (d,p) так, что р может использовать d. Но множество таких пар есть подмножество D‘P. Если, например, мы рассмотрим некоторую программу р_Р, то она связывает некоторые элементы из Д с результатами из R. Тогда имеет смысл изучать некоторое подмножество Д‘R‘P таких элементов (d, p, r), что результат r получен из d при помощи программы р. Это уже отношение между элементами трех множеств.

Теперь можно переходить к формальным рассмотрениям:

Основные понятия

Определение 1: n-местным отношением R на множествах А₁,A₂,…,A_n называется подмножество прямого произведения A₁‘A₂‘…‘ A_n . Другими словами, элементы x₁, x₂, ..., x_n связаны отношением R тогда и только тогда, когда (x₁, x₂, ..., x_n)_R_ A₁‘A₂‘…‘ A_n.

Наиболее часто встречаются отношения при n=2. В этом случае они называются бинарными отношениями. Таким образом, бинарное отношение на множествах А и В есть просто подмножество А‘В. Если же А=В, то это подмножество А². В этом случае будем говорить, что отношение задано на множестве А. В основном мы будем изучать бинарные отношения.

Пример:

Пусть А={1,2,3,4,5,6,7,8,9,10}. Зададим R на А: R={(x,y)| x,y_A) x делитель y ) x_5}. Его можно выписать в явном виде: R={(1,1), (1,2) ,..., (1,10), (2,2), (2,4), (2,6), (2,8), (2,10), (3,3), (3,6), (3,9), (4,4), (4,8), (5,5), (5,10)}.

В общем случае количество различных отношений на множестве А зависит от |A|. Большая часть этих отношений не представляет особого интереса. Ниже дадим определение трех отношений, которые имеют важное значение при построении теории бинарных отношений.

Определение 2: Пусть А - произвольное непустое множество. Отношение I_A={(a,a)| a_A} называется тождественным отношением на А. Отношение U_A={(a,b)| a_A ) b_A} называется универсальным отношением на А, то есть U_A=A². Кроме того, Æ _ А², значит оно тоже является(определяет) отношением на А и называется пустым отношением.

Пусть R - бинарное отношение на множествах А и В. Поскольку R всего лишь подмножество А‘В, то может случиться так, что не все а_А и b_B находятся в отношении R.поэтому имеет смысл ввести следующие понятия:

Определение 3: Областью определения D(R)бинарного отношения R_A‘B называется такое подмножество А, что D(R)={x| (x,y)_R}. Областью значений E(R)бинарного отношения называется такое подмножество В, что E(R)={y|(x,y)_R}. Если R_A², то D(R)_A и E(R)_A.

Пример: Если R есть отношение из предыдущего примера, то D(R)={1,2,3,4,5}, E(R)=A.

Существует три основных способа записи того, что элементы а и b находятся в некотором отношении. С одним из них мы уже встречались:

1. (a,b)_R. Другой способ использует строчные греческие буквы:

2. a R b, «а связано с b отношением R», то есть высказывание a R b истинно. Это удобно, когда для конкретного отношения существуют специальный символ. Например, r_N² и r={(x,y): x<y}, здесь вместо 6 r 7 можно писать 6<7.

3.b_R (a) это функциональная запись отношения.

Из заданного бинарного отношения можно построить другие отношения, например обратное к R.

Определение 4: Пусть R — бинарное отношение. Обратным (инверсным)к R отношением называется следующее отношение: R^-1={(x,y)| (y,x)_R}.

Следовательно, если R _ A‘B , то R^-1 _ B‘A. Тогда из определения получаем, что D(R^-1)=E(R) и E(R^-1)=D(R).

В дальнейшем будем обозначать D(R)=D_R, E(R)=E_R.

Пример: Пусть X={2,4,6,8}, r={(x,y)| x,y_X ) x<y}. Выпишем r и r^-1:

r={(2,4), (2,6), (2,8), (4,6), (4,8), (6,8)}, D_r={2,4,6}, E_r={4,6,8},

r^-1={(4,2), (6,2), (8,2), (6,4), (8,4), (8,6)}.

В заключение этого параграфа рассмотрим некоторые методы графического изображения отношений, заданных на «небольших» множествах. Поскольку, при решении конкретной задачи, особенно на первом этапе, рисунок может оказаться весьма полезным.

Пусть X={a, b, c, d, e}. Рассмотрим отношения I_X, U_X и R={(a,b), (a,c), (b,d), (c,e), (e,b)}.

На координатной плоскости:

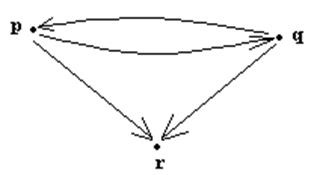
Одним из наиболее часто встречающихся методов изображения отношений является изображение с помощью графа :

Это изображение более наглядно и для изучения свойств небольших отношений является достаточно эффективным.

Свойства отношений

Об общих отношениях как подмножествах прямых произведений можно сказать очень мало. Поэтому есть смысл изучать только специальные отношения, обладающие некоторыми свойствами. Здесь мы разберем основные свойства бинарных отношений.

Определение 1: Пусть R- бинарное отношение на множестве A. Тогда

a) R - рефлексивно, если " xÎA x R x

b) R - симметрично, если x R y Þ y R x

c) R - транзитивно, если x R y Ù y R z Þ x R z

d) R - антисимметрично, если x R y Ù y R x Þ x=y.

Рассмотрим примеры:

1. Пусть r= {(x, y)| x, yÎN и x – делитель y}

s={(x, y)| x, yÎN и x£y}

t={(x, y)| x, yÎN\{1} и (x и y имеют общий делитель)}.

Изучим свойства этих отношений:

r - рефлексивно: x делитель x "xÎN; несимметрично: 2 делитель 4, 4 – не делитель 2; транзитивно: x делитель y, y делитель z Þ x делитель z; антисимметрично: если x делит y и y делит x, òî x=y.

s - рефлексивно, несимметрично, транзитивно, антисимметрично;

t -рефлексивно, симметрично, но не транзитивно(3 и 6, 6 и 8) и не антисимметрично

Замечание: свойства симметричности и антисимметричности не являются взаимоисключающими. Отношение I_X на любом множестве X является симметричным и антисимметричным.

2. P- множество всех людей. Зададим отношение B: x B y Û x брат y. Рассмотрев семью, состоящую из двух братьев p и q и сестры r, имеем:

pBr, но не r B p- B не симметрично. Оно и не антисимметрично pBq, qBp, но p¹q. Граф этого от ношения приведен ниже.

3. Задача: Найти ошибку в рассуждении: Если отношение R симметрично и транзитивно, то оно рефлексивно:

Доказательство: aRbÙbRaÞaRa.

Построить контрпример на множестве {1,2,3}.

Не нашли, что искали? Воспользуйтесь поиском по сайту: