
|
|
Отношение эквивалентности.Во многих вычислительных задачах берутся большие множества и разбиваются таким образом, чтобы все интересующие нас ситуации можно было исследовать на нескольких правильно выбранных примерах. Определение 1:Пусть A ¹ Æ и {Ai},i= Например, {A, B}- покрытие AÈB; {A, AÈB, B, C}-покрытие AÈBÈC. Замечание: В общем случае покрытие может быть и бесконечным. однако с точки зрения изучения конкретных свойств такая ситуация не вызывает энтузиазма. Определение 2: Разбиением непустого множества А называется такое его покрытие Например, {A, A’} – разбиение U. {AÇB, AÇB’, A’ÇB, A’ÇB’} – разбиение U, {A\B, AÇB, B\A} – разбиение AÈB. Организовать разбиение непустого множества можно при помощи отношений, которые ведут себя подобно отношениям равенства на множестве чисел или множеств. Определение 3: Бинарное отношение на множестве называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Примеры: 1. На множестве всех треугольников: {(x, y)| x и y имеют одинаковую площадь} 2. На множестве всех программ: {(a, b)| a, b вычисляют одну и ту же функцию на конкретной машине} Определение 4: Пусть R – отношение эквивалентности на множестве А и xÎA. Классом эквивалентности порожденным элементом х называется множество {y| xR y}=[x]R. Определение 5: Любой элемент класса эквивалентности называется представителемэтого класса. Полной системой представителей называется множество представителей, по одному из каждого класса. Пример 3: N – натуральные числа, s – фиксированный элемент. На Z определено отношение: rs= {(x, y)| x-y=ns, nÎZ}. Отношение сравнения по модулю s ( запись: xºy(mod s)). Нетрудно проверить, что отношение сравнения по модулю s, есть отношение эквивалентности на множестве Z. Пусть, например, s=10. Тогда: [1] = {11,21,-9,10 976 631,.... } [1066] = {66,226,-24,... } На самом деле есть всего 10 классов эквивалентности по этому отношению, а числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 образуют полную систему представителей. Классы эквивалентности по этому отношению эквивалентности называют классами вычетов по модулю s. Определение 6: Фактор-множеством множества А по отношению эквивалентности R называется множество всех классов эквивалентности по этому отношению и обозначается A/R. Множество классов вычетов по модулю s обозначают Zs. Имеет место Теорема (о разбиении): Пусть R - отношение эквивалентности на непустом множестве А. Тогда фактор-множество A/R является разбиением множества А. Доказательство: "xÎA( xÎ[x]R). Надо доказать, что каждый элемент множества А принадлежит в точности одному классу. То есть, докажем, что если классы имеют хотя бы один общий элемент, то они совпадают. Пусть cÎ[a] и cÎ[b]. Пусть xÎ[a], но тогда x R a, a R c, c R b Þ x R b(транзитивность R). Значит, [a] Ì [b]. ( где рефлексивность? а она есть!) Аналогично [b] Ì [a]. Что и требовалось доказать. Имеет место и обратное утверждение. Пусть S- разбиение множества А и Rs – бинарное отношение на A, такое что: R={(x,y)ïx и y принадлежат одному элементу разбиения }, тогда R , будем называть– отношением, определяемым разбиением S. Теорема (обратная): Отношение R на А, определяемое разбиением S, является отношением эквивалентности на А, причем A/Rs=S.(самостоятельно) Упражнения: 1. Пусть А- конечное множество. Какие отношения эквивалентности дают наибольшее и наименьшее число классов эквивалентности. 2. Если {A1, A2, ..., An}- разбиение А и А конечно, то
Отношение порядка. Из понятия равенства (например, чисел) возникает математическое понятие эквивалентности. А из понятия неравенства возникает другой тип отношений, которые называются отношениями порядка. Определение 1: Частичным порядкомна множестве А называется бинарное отношение, которое рефлексивно, антисимметрично и транзитивно. Частичный порядок - это обобщение отношения £ на R. Можно ввести понятие строгого порядка, соответствующего отношению < на R. Отношение строгого порядка - только транзитивно(оно еще и антирефлексивно). Если задан £, то можно определить <: a<b Û a£b Ù a¹b. Если задан <, то можно определить £: a£b Û a<b Ú a=b. Множество, на котором задано отношение порядка, будем обозначать (X, £) (или (X, <), если порядок строгий). Определение 2: Множество, на котором задано отношение порядка, называется частично упорядоченным. Пример: A - множество. (P(A),Í), легко проверить, что отношение Í является отношением порядка на P(A). Определение 3: Отношение порядка R на А называется полным (линейным) порядком, если " x, yÎA (xR y Ú yR x). Множество (A, R) называется линейно упорядоченным. Примеры: 1. отношение £ на R является отношением полного порядка. Таким образом (R, £) - линейно упорядочено. 2. а вот (P(A),Í) не является линейно упорядоченным 3. x£y Û y Определение 4: пусть (A, £) – частично упорядоченное множество. Элемент аÎА называетсянаименьшим /наибольшим/ в А, если " xÎA (a£ x) /x £ a /. Элемент bÎА называется минимальным /максимальным/ если " xÎA (x£ a Þ x=a) /a £ x Þ a=x /. Задача: Доказать, что для линейно упорядоченного множества понятия наибольшего (наименьшего) и максимального (минимального) элементов совпадают. Привести пример частично упорядоченного множества, где они не совпадают.
Композиция отношений Пусть заданы множества A, B и C и отношения S между A и B (то есть SÌA´B) и R между B и C (RÌB´C). Определим новое отношение между A и C следующим образом: Определение 1: Множество всех пар (x, y), таких, что существует zÎB такое, что (x, z)Î S и (z, y)Î R называется композицией отношенийS и R . Обозначается: R o S . Таким образом, R o S Ì A ´ C . R oS = {(x, y)| $zÎB((x,z)ÎSÙ(z,y)ÎR)} или x R o Sy Û $zÎB(xSzÙzRy). Пример 1: Пусть A={1, 2, 3}, B={1, 2, 3, 4, 5, 6}, C={3, 6, 9, 12}, s ={(1,2), (2,4), (3,6)}, r={(1,3), (2,6), (3,9), (4,12)}. Тогда r o s={(1,6), (2,12)}. Проиллюстрируем ситуацию на картинке:
Пример 2: Пусть s и r - отношения на N такие, что
Dros={xïxÎNÙ x+1=y2}={3,8,15,24,...}. В случае, когда отношение задано на множестве, оно может быть скомбинировано с самим собой: sos = s2 = {(x,x+2)½xÎN} и ror = r2 = {(x4,x)½xÎN}. Используя это обозначение, можно определить энную степень отношения:
Например, для отношений из примера 2 имеем:
Хотелось бы дополнить аналогию с умножением. Для этого введем следующее естественное определение: Определение 2:Бинарные отношения называются равными, если они равны как подмножества, то есть R=S, если"x,y((x,y)ÎRÛ(x,y)ÎS). Понятно, что отношения должны быть определены на одних и тех же множествах. Теорема (свойства композиции отношений): Для любых бинарных отношений R, S, T имеют место равенства: 1. (RoS)oT = Ro(SoT) 2. (RoS)-1 = S-1o R-1 Доказательство: 1) Для любых x и y имеем: x(RoS)oTy º $z(xTzÙ(zRoSy)) º $z$t(xTzÙ(zStÙtRy)) º $z$t((xTzÙzSt)ÙtRy) º $t(($z(xTzÙzSt))ÙtRy) º $t((xSoTt)ÙtRy) º xRo(SoT)y. 2) x(RoS)-1y º yRoSx º $z(ySzÙzRx) º $z(xR-1zÙzS-1y) º xS-1oR-1y. Что и требовалось доказать. Замечание: если R - отношение на множестве A, то ясно, что IAoR=RoIA=R. То есть IA ведет себя как единица при умножении чисел. Однако полной аналогии провести нельзя. Поскольку, например, коммутативность, в общем случае места не имеет, так как RoS может быть определено, а SoR нет. Также как и не всегда имеет смысл равенство R-1oR=RoR-1= IA.
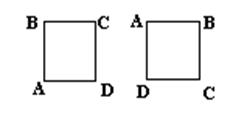
Замыкание отношений Понятие замыкания является фундаментальным математическим понятием и используется в большинстве разделов математики. Проиллюстрируем это понятие на общем примере: возьмем объект x0 и процесс P, который, будучи примененный последовательно, порождает некоторое множество и, значит, определяет последовательность x1, x2, ..., xn, ... так, что x1ÎP(x0), x2ÎP(x1),..., xnÎP(xn-1),... Определение 1: множество, содержащее все элементы всех последовательностей, которые могут быть получены при помощи процесса P и начинающиеся с x0, называется замыканием процессаP относительно x0. Ясно, что результат будет заключаться в нахождении Рn(x0) при некотором n. Это n мы заранее не знаем, оно зависит от самого процесса. Более того, если мы возьмем элемент y из этого замыкания и будем применять к нему процесс р, то не получим ничего нового. То есть множество таким путем расширено быть не может - оно замкнуто! Пример:Возьмем квадрат S, обозначенный ABCD и рассмотрим процесс r, заключающийся в повороте квадрата по часовой стрелке на 90°:
Пусть отношение A задано на некотором множестве. Тогда: Определение 2: Транзитивным замыканием отношения A на данном множестве называется отношение A+: Таким образом, из не транзитивного отношения A на некотором множестве можно построить транзитивное A+. Примеры: 1. r - отношение на N: r={(x, y)| y=x+1}, тогда r+={(x, y)| x<y} 2. s на Q: s={(x, y)| x<y}, тогда s+=s 3. t наQ: t={(x, y)| x×y=1}, тогда r+={(x, x)| x¹0} 4. Пусть L - множество станций лондонского метро; L={a, b, c} последовательные станции. N={(x, y)| y следует за x}.Значит (a, b), (b, c) ÎN; кроме того (a, a), (b, b), (c, c), (a, c) Î N2. Значит, N+=L´L Вообще говоря, транзитивное замыкание не является рефлексивным (пример 2). Пусть A - отношение на X. Положим A0=IX. Определение 3: Рефлексивным замыканием А* отношения A называют отношение Примеры: 1. r*={(x, y)| x£y} 2. s*={(x, y)| x£y} 3. t* = t+È{(0,0)} 4. N*=N+

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 совокупность подмножеств таких, что A=
совокупность подмножеств таких, что A=  . Тогда совокупность этих подмножеств называется покрытием множества A.
. Тогда совокупность этих подмножеств называется покрытием множества A. 

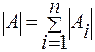 .
. x на множестве N не является полным порядком
x на множестве N не является полным порядком
 , где nÎN, n>1.
, где nÎN, n>1.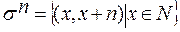 ,
, 


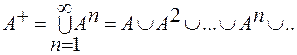
 . То есть
. То есть  .
.