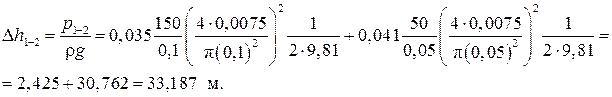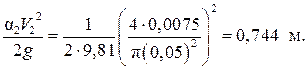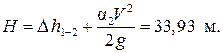|
|
Истечение жидкости из насадковНасадком называют короткую трубку длиной (3 ... 4) d, прикрепленную к отверстию. Существуют следующие виды насадков: цилиндрические – внутренний (рис. 24, а) и внешний (рис. 24, б); конические – сходящийся (рис. 24, в) и расходящийся (рис. 24, г); коноидальные (рис. 24, д).
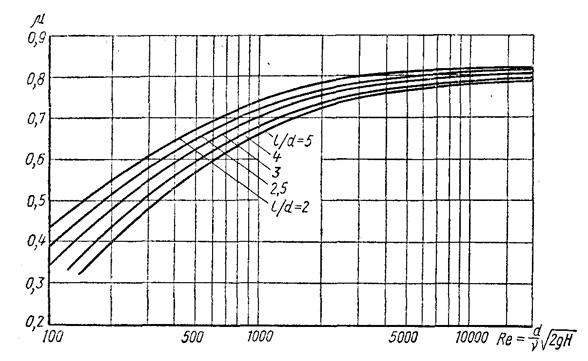
Цилиндрический внешний насадокшироко применяют на практике, например в гидротехнических сооружениях. Так, водоспуски в плотинах, трубы под насыпями рассчитывают по теории истечения жидкости через насадки. При этом происходит гидравлическое явление, физическая сущность которого заключается в следующем. При входе жидкости в отверстие насадка вследствие изгиба линий токов происходит сжатие струи и на некотором расстоянии от входа в насадке образуется водоворотная зона. Вследствие сжатия струи внутри насадка создается вакуум, величина которого зависит от скорости течения, а следовательно, и от величины напора, над центром входного отверстия в насадок. Полный действующий напор насадка как бы увеличивается за счет вакуума и складывается из напора над центром тяжести входного отверстия насадка и величины вакуума в сжатом сечении. Вместе с тем присоединение насадка к отверстию дает дополнительные потери напора по сравнению с истечением жидкости через отверстие без насадка, вызываемые внезапным расширением потока жидкости внутри насадка и трением потока о его внутреннюю поверхность. Поэтому, чтобы дополнительные потери в насадке не были большими, необходимо его длину делать в пределах (3 ... 4) d. Такой насадок называют насадком Вентури. Здесь d — внутренний диаметр насадка. Зависимость коэффициента расхода от напора (числа Рейнольдса) приведена на рис. 25.
Рис. 25 Цилиндрический внутренний насадок показан на рис. 24, а. Физическая сущность гидравлического явления в этом насадке аналогична явлению во внешнем цилиндрическом насадке. Но коэффициенты сжатия, скорости и расхода при истечении жидкости через насадок полным входным сечением имеют следующие осредненные значения: φ= 0,71; ε = 1 и μ = 0,71. Таким образом, внутренний цилиндрический насадок имеет большие гидравлические сопротивления, чем внешний, что и приводит к уменьшению коэффициента скорости, а следовательно, и к уменьшению коэффициента расхода μ до 0,71. Это указывает на худшие гидравлические характеристики у внутреннего цилиндрического насадка по сравнению с внешним, поэтому он реже применяется на практике. Конический сходящийся насадок (см. рис. 24, в). Имеет форму конуса, сходящегося по направлению к выходу струи. Конические сходящиеся насадки применяются там, где необходимо иметь большую удельную кинетическую энергию, например: в пожарных брандспойтах, гидромониторах, фонтанах, эжекторах и т.п. В этом насадке коэффициент расхода увеличивается в результате уменьшения гидравлических сопротивлений и, главным образом, уменьшения эффекта внезапного расширения потока. Значение коэффициентов гидравлических сопротивлений в конически сходящихся насадках достигает 0,06. Опыты показывают, что коэффициент расхода μ в этих насадках зависит от угла конусности θ. При возрастании θ от 0 до 13°24' коэффициент μ также увеличивается от 0,829 до 0,946; при дальнейшем увеличении θ коэффициент μ уменьшается. При угле θ = 13°24' коэффициент расхода имеет максимальное значение и достигает значения μ = 0,946. При угле θ = 13°24' сжатие струи в сечении С – С практически исчезает. Увеличение угла конусности θ свыше 13°24' приводит к некоторому уменьшению коэффициента расхода μ, так как при этом происходит дополнительное сжатие струи при выходе из насадка. Конический расходящийся насадок (см. рис. 24, г) применяется в тех случаях, когда нужно за счет уменьшения скорости значительно увеличить давление, например в реактивных гидротурбинах, центробежных насосах и др. Скорость в сжатом сечении С – С больше, чем в выходном, и в результате этого давление в выходном сечении насадка больше, чем в сжатом сечении (что следует из уравнения Бернулли). В конически расходящемся насадке сжатие струи и вакуум больше, чем у цилиндрического внешнего, причем с увеличением угла конусности θ вакуум возрастает. Чем больше угол конусности θ, тем легче струе оторваться от стенок насадка. Поэтому для надежности работы без срыва вакуума в конически расходящихся насадках допускается угол конусности θ, равный 5 – 7°. Потери энергии в коническом расходящемся насадке на внезапное расширение значительно больше потерь в других насадках, поэтому коэффициент расхода μ, отнесенный к выходному сечению насадка, диаметром dв при θ = 5…7°, равен примерно 0,5, а коэффициент сжатия Коноидальный насадок (рис. 24, д). У коноидального насадка устраняется недостаток, имеющийся у конического сходящегося при θ > 13°24', т. е. сжатия струи при выходе из насадка не происходит и коэффициент сжатия Для получения больших значений коэффициентов μ и φ необходимо, чтобы входная часть насадка была выполнена очень тщательно, а это практически вызывает трудности и поэтому он не получил широкого распространения на практике.
Примеры решения задач
Задача 1.В бак, разделенный перегородкой на два отсека, подается вода в количестве Q = 4 л/с (рис. 26). В перегородке бака имеется цилиндрический насадок, диаметром d1 = 50 мм и длиной l = 3d1. Вода из второго отсека через отверстие d2 = 32 мм поступает в атмосферу. Определить высоты H1 и H2.
Рис. 26
Решение. Расход воды через отверстие определяется из уравнения:
где Тогда необходимый расход Q обеспечивается напором, создаваемым столбом жидкости высотой H2:
Расход воды, истекающей под уровень через насадок из первого во второй отсек, определяется аналогично:
где Тогда необходимый расход Q обеспечивается напором, создаваемым столбом жидкости высотой H1 – H2:
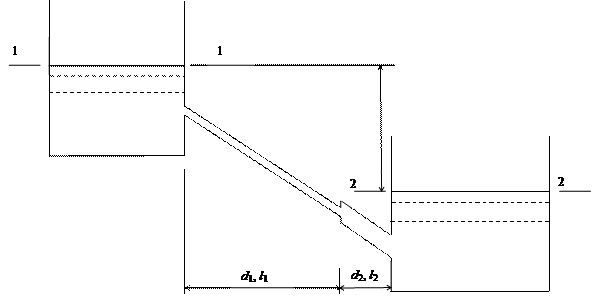
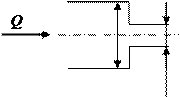
Высота H1 = 2 + 0,26 = 2,26 м. Задача 2. Определить расход воды в горизонтальной трубе (рис. 27), соединяющей два резервуара и имеющей два участка: Первый участок диаметром d1 = 10 мм и длиной l1 = 50 мм. Второй участок диаметром d2 = 12 мм и длиной l2 = 50 мм. Возвышение воды над осью трубки в левом сосуде h1 = 1,5 м, а в правом h2 = 1,2 м. Показания манометров p1 = 0,21 МПа, p2 = 0,12 МПа. Возвышение оси трубки над дном сосудов h = 30 мм.
Рис. 27
Решение.Расход воды через отверстие определяется из уравнения Бернулли для сечений 1-1 и 2-2:
где потери давления
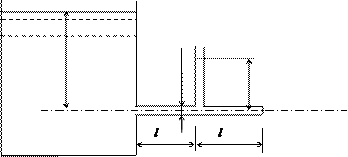
для первого участка: для второго участка: ξ1 – вход в первый участок (внезапное сужение русла) (рис. 28):
ξ2 – переход от первого участка ко второму (внезапное расширение русла) (рис. 29):

резервуар (внезапное расширение русла):
Общие потери давления будут:
с другой стороны, из уравнения Бернулли
Тогда
Задача 3. Определить потери напора на трение по длине водопровода диаметром d = 15 см, длиной l = 1 км, если расход воды Q = 35 л/с.
Решение.Коэффициент потерь на трение по длине λ определим по универсальной формуле Альтшуля: Для расчета примем эквивалентную шероховатость внутренней поверхности трубы Средняя скорость воды Число Рейнольдса
Задача 4. Истечение воды из закрытого вертикального сосуда в атмосферу происходит при постоянном геометрическом напоре h = 3 м через внешний цилиндрический насадок диаметром d = 8 см (рис. 30). Определить давление, необходимое на свободной поверхности воды в сосуде, чтобы расход при истечении Q = 50 л/с. Решение.Сужение струи при истечении из насадка не происходит, то есть коэффициент сжатия струи
С другой стороны:
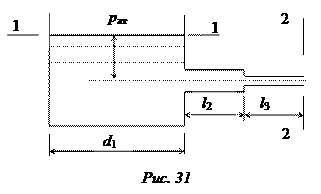
Задача 5. Определить H при вытекании воды из сосуда для обеспечения расхода воды Q = 7,5 л/с (рис. 31), если d1 = 5 м, d2 = 0,1 м, d3 = 0,05 м, l2= 150 м и l3 = 50 м.
где z1 = H, z2 = 0, p1= p2 = pат . Из-за большой протяженности трубопровода местными потерями можно пренебречь, тогда потери давления:
Предположим, что коэффициент потерь на трение по длине λ не зависит от числа Рейнольдса: для первого участка: для второго участка: Общие потери напора будут:
Скоростной напор
КОНТРОЛЬНОЕ ЗАДАНИЕ 2
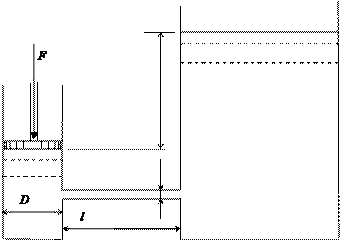
Задача 1.Поршень диаметром D движется равномерно вниз в цилиндре, подавая жидкость в открытый резервуар с постоянным уровнем. Диаметр трубопровода d, длина l. Когда поршень находится ниже уровня жидкости в резервуаре на H, потребная для его перемещения сила равна F. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии. Коэффициент гидравлического трения трубы принять l = 0,03. Коэффициент сопротивления входа в трубу xвх = 0,5. Коэффициент сопротивления выхода в трубу xвых = 1,0.
Рис. 32 Таблица 12
Задача 2. Из открытого резервуара, в котором поддерживается постоянный уровень жидкости, по трубопроводу, имеющему два участка, жидкость при температуре 20 0С течет в другой резервуар, расположенный ниже на высоту H. Определить расход жидкости. В расчетах принять, что местные потери напора составляют 10 % потерь по длине (рис. 33, табл. 13).
Рис. 33 Таблица 13
Задача 3. При истечении жидкости из резервуара в атмосферу по горизонтальной трубе, диаметра d и длиной 2l, уровень в пьезометре, установленном посередине длины трубы, равен h (рис. 34, табл. 14). Определить расход Q и коэффициент гидравлического трения трубы l, если статический напор в баке постоянен и равен H. Построить напорную и пьезометрическую линии. Сопротивлением входа в трубу пренебречь.
Рис. 34 Таблица 14
Задача 4. Определить длину трубы l (рис. 35, табл. 15), при которой расход жидкости Q из резервуара в атмосферу будет в два раза меньше, чем из отверстия того же диаметра d. Напор над отверстием равен H. Коэффициент гидравлического трения трубы принять l = 0,025.
Рис. 35 Таблица 15
ПРИЛОЖЕНИЕ 2

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
.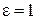 . Входная часть таких насадков выполнена по форме струи, вытекающей из отверстия, а выходной участок имеет цилиндрическую форму. Благодаря этому увеличиваются коэффициент скорости и коэффициент расхода. Можно принять для коноидальных насадков μ = φ = 97 ... 0,99.
. Входная часть таких насадков выполнена по форме струи, вытекающей из отверстия, а выходной участок имеет цилиндрическую форму. Благодаря этому увеличиваются коэффициент скорости и коэффициент расхода. Можно принять для коноидальных насадков μ = φ = 97 ... 0,99.


 ,
,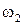 – площадь поперечного сечения отверстия d2, μ2 = 0,63 – коэффициент расхода для тонкого отверстия.
– площадь поперечного сечения отверстия d2, μ2 = 0,63 – коэффициент расхода для тонкого отверстия. м.
м. ,
,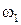 – площадь поперечного сечения насадка d1, μ1 = 0,81 – коэффициент расхода для насадка длиной l = 3 d1.
– площадь поперечного сечения насадка d1, μ1 = 0,81 – коэффициент расхода для насадка длиной l = 3 d1. м.
м.



 ,
,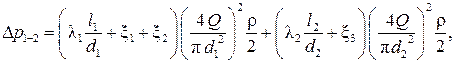
 – коэффициент потерь на трение по длине. Предположим, что коэффициент потерь на трение по длине λ не зависит от числа Рейнольдса:
– коэффициент потерь на трение по длине. Предположим, что коэффициент потерь на трение по длине λ не зависит от числа Рейнольдса: ,
,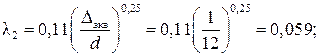


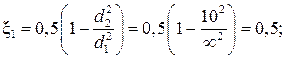


 ξ3 – выход из второго участка во второй
ξ3 – выход из второго участка во второй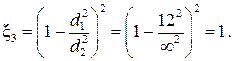

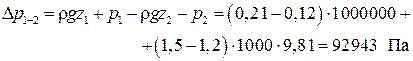
 м3/с.
м3/с.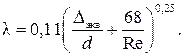
 = 1 мм, кинематическую вязкость ν = 10-6 м2/с.
= 1 мм, кинематическую вязкость ν = 10-6 м2/с. м/с.
м/с. .
.
 м.
м.

 , коэффициент расхода
, коэффициент расхода 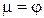 равен коэффициенту скорости
равен коэффициенту скорости  . Тогда средняя скорость:
. Тогда средняя скорость: м/с.
м/с. ,откуда
,откуда 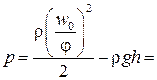
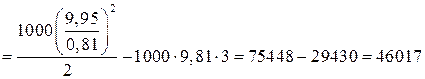 Па.
Па.
 Решение. Расход воды определяется из уравнения Бернулли для сечений 1-1 и 2-2:
Решение. Расход воды определяется из уравнения Бернулли для сечений 1-1 и 2-2: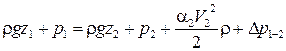 ,
,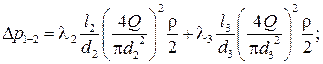
 – коэффициент потерь на трение по длине.
– коэффициент потерь на трение по длине.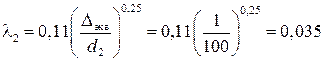 ,
, .
.