|
Потери напора в местных сопротивлениях
Кроме потерь энергии или напора по длине существуют потери, вызываемые изменением живого сечения или направления потока в местных сопротивлениях.
В местных сопротивлениях возникают водоворотные зоны и зоны интенсивного перемешивания потока жидкости. Потери напора определяются формулой Вейсбаха:  , где ξ – коэффициент местного сопротивления (табл. 10). , где ξ – коэффициент местного сопротивления (табл. 10).
Величина коэффициента местного сопротивления зависит от числа Рейнольдса: Re < 10000. Местные сопротивления оказывают влияние друг на друга при близком их взаимном расположении. Эти и другие эффекты в данных методических указаниях не представлены.
Таблица 10
| Местное сопротивление
| ξ
| | Внезапное расширение
| 

| | Внезапное сужение
| 

| | Постепенное расширение (диффузор)
| α0
|
|
|
|
|
|
| | K
| 0,02
| 0,05
| 0,1
| 0,14
| 0,16
| 0,22
| | α0
|
|
|
|
|
|
| | K
| 0,3
| 0,42
| 0,62
| 0,72
| 0,85
|
|
|  ,
где ,
где  . .

| | Постепенное сужение (конфузор)
| α0
|
|
|
|
|
|
| | KПС
| 0,4
| 0,25
| 0,16
| 0,18
| 0,27
| 0,36
|
| 

| | Внезапный поворот трубы
|
| α0
|
|
|
| | K
| 0,12
| 0,3
| 0,5
| | α0
|
|
|
| | K
| 0,82
| 1,37
| 2,2
|
| Продолжение табл. 10
| Местное сопротивление
| ξ
| | Закругленное колено
|
 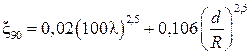
| α0
|
|
|
| | a
| 0,4
| 0,55
| 0,65
| | α0
|
|
|
| | a
| 0,75
| 0,83
| 0,88
| | α0
|
|
|
| | a
| 0,95
| 1,0
| 1,13
| | α0
|
|
|
| | a
| 1,2
| 1,27
| 1,33
|
| | Диафрагма
| d0/d2
| 0,3
| 0,4
| 0,5
| 0,6
| | ε
| 0,613
| 0,616
| 0,621
| 0,628
| | ξ
|
| 83,3
| 29,5
| 11,6
| | d0/d2
| 0,7
| 0,8
| 0,9
| 1,0
| | ε
| 0,64
| 0,667
| 0,718
|
| | ξ
| 4,8
| 1,76
| 0,52
|
|
|
 ,
где ,
где  – коэффициент сжатия струи – коэффициент сжатия струи
| | Задвижка
|
 – аналогично диафрагме
– аналогично диафрагме
| | Вентиль с вертикальным шпинделем
|
| dу, мм
| ξ
| |
|
| |
|
| | 25,32
|
| |
|
| | 50 и более
|
|
| Продолжение табл. 10
Истечение жидкости через отверстия и насадки
Наибольший интерес представляет задача о связи между напором в резервуаре и расходом жидкости через отверстие и насадок.
Истечение жидкости из отверстия в тонкой стенке
Стенка считается тонкой, если ее толщина  , где d0 – диаметр отверстия. , где d0 – диаметр отверстия.
   При выходе из отверстия струя сжимается. Сжатие обусловлено тем, что существует составляющая скорости в направлении перпендикулярном движению. В результате наличия инерции максимальное сужение наблюдается за отверстием (примерно на расстоянии При выходе из отверстия струя сжимается. Сжатие обусловлено тем, что существует составляющая скорости в направлении перпендикулярном движению. В результате наличия инерции максимальное сужение наблюдается за отверстием (примерно на расстоянии  (рис. 21). (рис. 21).
Коэффициент сжатия струи  зависит от вида отверстия. зависит от вида отверстия.
    Различаются: Различаются:
1) Отверстия с совершенным и несовершенным сжатием. Отверстия с совершенным сжатием бывают при расположении отверстия до границ жидкости не менее трех размеров (рис. 22).
В отверстиях с несовершенным сжатием стенки частично направляют движение жидкости к отверстию, поэтому степень сжатия для таких отверстий меньше:
 , ,
где p – периметр, n – часть периметра, по которой нет сжатия.
2) Большие и малые отверстия. Малое отверстие характеризуется условием:  , где H – напор над центром отверстия. При этом условии скорость по высоте сечения не изменяется и , где H – напор над центром отверстия. При этом условии скорость по высоте сечения не изменяется и 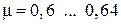 . Для большого отверстия коэффициент расхода μ, о котором речь пойдет ниже, приведен в табл. 11. . Для большого отверстия коэффициент расхода μ, о котором речь пойдет ниже, приведен в табл. 11.
Действительная скорость истечения определяется из уравнения Бернулли:
 , ,
где  – коэффициент Кориолиса ( – коэффициент Кориолиса (  ); );
 – коэффициент местного сопротивления (отверстия); – коэффициент местного сопротивления (отверстия);
 – давления на поверхности жидкости и на выходе из отверстия. – давления на поверхности жидкости и на выходе из отверстия.
 , где , где  – коэффициент скорости. – коэффициент скорости.
Таблица 11
| Типы больших отверстий
| μ0
| | Отверстия средних размеров со сжатием струи со всех
сторон при отсутствии направляющих стенок
| 0,65
| | Большие отверстия с несовершенным, но всесторонним
сжатием
| 0,70
| | Донные отверстия без сжатия по дну со значительным
влиянием бокового сжатия
| 0,65 – 0,70
| | Донные отверстия без сжатия по дну и уменьшенным
влиянием бокового сжатия
| 0,70 – 0,75
| | То же без сжатия по дну и с весьма плавными боковыми
подходами
| 0,80 – 0,85
| | То же без сжатия по дну и с весьма плавными боковыми
подходами к отверстию со всех сторон
| 0,90
| 
Расход определяется как произведение действительной скорости на фактическую площадь сечения струи:
 , ,
где  – коэффициент расхода. – коэффициент расхода.
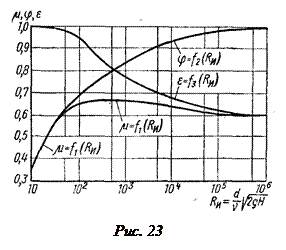
На рис. 23 показаны зависимости коэффициентов φ, ε и μ для круглого отверстия от Reи, рассчитанного по идеальной скорости истечения.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , где ξ – коэффициент местного сопротивления (табл. 10).
, где ξ – коэффициент местного сопротивления (табл. 10).










 ,
где
,
где  .
.







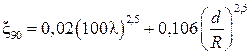



 ,
где
,
где  – коэффициент сжатия струи
– коэффициент сжатия струи


 – аналогично диафрагме
– аналогично диафрагме


 ,
где δ – эквивалентная высота сварного стыка
,
где δ – эквивалентная высота сварного стыка




 , где
, где  – коэффициент скважности,
– коэффициент скважности,



 , где d0 – диаметр отверстия.
, где d0 – диаметр отверстия.

 При выходе из отверстия струя сжимается. Сжатие обусловлено тем, что существует составляющая скорости в направлении перпендикулярном движению. В результате наличия инерции максимальное сужение наблюдается за отверстием (примерно на расстоянии
При выходе из отверстия струя сжимается. Сжатие обусловлено тем, что существует составляющая скорости в направлении перпендикулярном движению. В результате наличия инерции максимальное сужение наблюдается за отверстием (примерно на расстоянии  (рис. 21).
(рис. 21). зависит от вида отверстия.
зависит от вида отверстия.


 Различаются:
Различаются: ,
, , где H – напор над центром отверстия. При этом условии скорость по высоте сечения не изменяется и
, где H – напор над центром отверстия. При этом условии скорость по высоте сечения не изменяется и 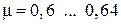 . Для большого отверстия коэффициент расхода μ, о котором речь пойдет ниже, приведен в табл. 11.
. Для большого отверстия коэффициент расхода μ, о котором речь пойдет ниже, приведен в табл. 11. ,
, – коэффициент Кориолиса (
– коэффициент Кориолиса (  );
); – коэффициент местного сопротивления (отверстия);
– коэффициент местного сопротивления (отверстия); – давления на поверхности жидкости и на выходе из отверстия.
– давления на поверхности жидкости и на выходе из отверстия. , где
, где  – коэффициент скорости.
– коэффициент скорости.
 ,
, – коэффициент расхода.
– коэффициент расхода.