
|
|
Сила давления жидкости на криволинейные стенки
Для криволинейных стенок (рис. 4), симметричных относительно вертикальной плоскости (большинство практических задач), сумма элементарных сил давления приводится к одной равнодействующей, лежащей в плоскости симметрии, или к паре сил, лежащих в той же плоскости. Величина и направление равнодействующей силы Величина горизонтальной составляющей силы давления на криволинейную стенку определяется по формуле
где Линия действия силы
где Вертикальная составляющая силы давления, воспринимаемая криволинейной стенкой, определяется по формуле
где
Рис. 4
Телом давления называется объем жидкости, ограниченный криволинейной поверхностью, вертикальной проектирующей поверхностью, построенной на контуре стенки, и пьезометричекой поверхностью. Сила Полная сила давления Угол наклона равнодействующей к горизонту определяется из формулы
Для стенок постоянной кривизны (цилиндрических, сферических) полная сила давления проходит через центр или ось кривизны стенки. При избыточном давлении на смоченной стороне стенки все составляющие и полная сила давления жидкости направлены от жидкости на стенку (изнутри наружу). В случае разряжения на смоченной стороне стенки силы направлены снаружи внутрь сосуда. При двухстороннем воздействии жидкости на стенку сначала определяются горизонтальные и вертикальные составляющие с каждой стороны стенки в предположении одностороннего воздействия жидкости, а затем суммарная горизонтальная и вертикальная составляющая от воздействия обеих жидкостей. Задача. Вертикальный цилиндрический сосуд заполнен водой, находящейся под избыточным давлением, показание пьезометра h = 5 м. Нижнее днище сосуда плоское, верхнее имеет форму полусферы (рис. 5).
Для верхнего полусферического днища объем тела давления равен фиктивному объему жидкости над этим днищем, показанному на рис. 5 штриховкой. Таким образом, имеем:
Сила, разрывающая сосуд по образующей цилиндра, определяется как горизонтальная составляющая равнодействующей силы давления на криволинейную поверхность по формуле
Задача. Прямоугольное донное отверстие плотины (рис. 6) закрывают сегментным затвором. Отверстие имеет размеры
Рис. 6
Решение. Горизонтальная составляющая сила определяется по формуле
Вертикальная составляющая сила определяется по формуле
Полная сила давления воды на затвор
Определим угол между

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 определяется по двум составляющим – горизонтальной и вертикальной.
определяется по двум составляющим – горизонтальной и вертикальной.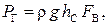
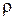 – плотность жидкости,
– плотность жидкости,  – ускорение свободного падения,
– ускорение свободного падения,  – расстояние по вертикали от центра тяжести вертикальной проекции стенки до пьезометрической плоскости О - О,
– расстояние по вертикали от центра тяжести вертикальной проекции стенки до пьезометрической плоскости О - О,  – площадь вертикальной проекции стенки.
– площадь вертикальной проекции стенки. , проходя через центр давления вертикальной проекции, лежит в плоскости симметрии и смещена относительно центра тяжести вертикальной проекции на расстояние
, проходя через центр давления вертикальной проекции, лежит в плоскости симметрии и смещена относительно центра тяжести вертикальной проекции на расстояние
 – эксцентриситет, смещение относительно центра давления;
– эксцентриситет, смещение относительно центра давления;  – момент инерции площади вертикальной проекции площади стенки относительно вертикальной оси, проходящей через центр тяжести проекции.
– момент инерции площади вертикальной проекции площади стенки относительно вертикальной оси, проходящей через центр тяжести проекции.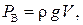
 – объем жидкости, называемый телом давления.
– объем жидкости, называемый телом давления.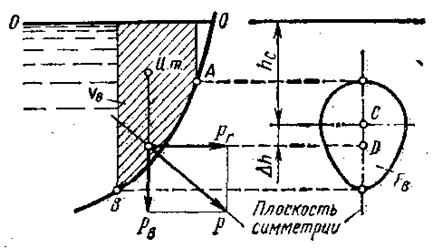
 проходит через центр тяжести объема
проходит через центр тяжести объема  .
.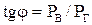 .
. Определить силу
Определить силу  = 2 м, высота цилиндрической части
= 2 м, высота цилиндрической части  = 3 м.
= 3 м.
 .
.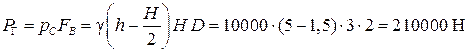 .
.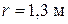 ,
,  . Напор на плотине
. Напор на плотине  Определить суммарную силу давления воды на сегментный затвор.
Определить суммарную силу давления воды на сегментный затвор.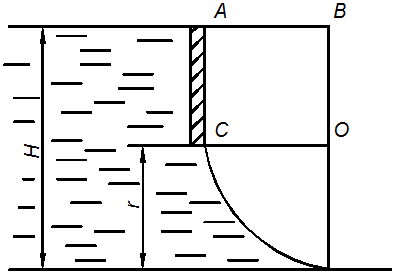
 .
.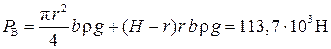
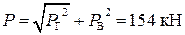
 ;
; 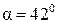 .
.