|
|
Разветвляющиеся алгоритмыНа практике алгоритмы линейной структуры встречается крайне редко. Чаще необходимо организовать процесс, который в зависимости от каких-либо условий проходит по той либо иной ветви алгоритма. Такой алгоритм называется разветвляющимся. В блок-схемах ветвление начинается на выходах элемента "Решение", с помощью которого в алгоритме выполняется проверка какого-либо условия. Количество ветвей тем больше, чем больше проверяемых условий. Для пояснения рассмотрим решение задачи нахождения значения функции z = y/x. На первый взгляд представляется, что алгоритм решения этой задачи имеет линейную структуру. Однако, если учесть, что делить на нуль нельзя из-за переполнения ячейки, то, во-первых, нужно из вычислений исключить вариант х = 0 и, во-вторых, проинформировать пользователя алгоритма о возникшей ошибке. Если этого не сделать, то при вычислениях может возникнуть аварийный выход до получения результата. В профессиональной практике аварийные завершения крайне нежелательны. т. к. к этому моменту уже может быть накоплено определенное количество результатов, которые окажутся необработанными и попросту пропадут. Можно привести другие примеры, когда аварийный останов компьютера может повлечь куда более серьезные последствия. Решение задачи представлено блок-схемой рис. 4.
В блоке 4 будет получен результат Z, затем в блоке б значения всех трех переменных будут отпечатаны и в блоке 7 алгоритм закончит работу. Если же ответ окажется положительным, то управление будет передано блоку 4. Выполняя команду блока 4, автомат выведет сообщение "Ошибка" и затем закончит работу в том же блоке 7.
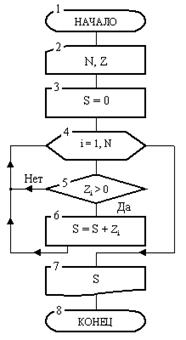
Рис. 4. Разветвляющийся алгоритм Циклические алгоритмы Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма. Различают циклы с наперед известным и наперед неизвестным количеством проходов. Пример 1. Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, ..., сумма которых больше числа К.
После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5. В нем при выполнении команды S = S + i производится сложение содержимого ячеек S и i, а результат записывается в ячейку S. Поскольку до операции сложения было S = 0, i = 1, то после операции будет S = 1. При записи нового значения старое содержимое ячейки S (нуль) стирается, а на его место записывается число 1. Нужно обратить внимание на то, что если бы до этой операции в блоке 3 не была выполнена команда S = 0 (записать нуль в ячейку S ), то при нахождении суммы S + 1 возникла бы ошибка, поскольку из ячейки S была бы извлечена константа, которая оказалась там после распределения памяти.
Рис. 5. Разветвляющийся алгоритм
После суммирования первого члена последовательности в блоке 6 выполняется проверка условия о превышении суммы S заданного числа К. Если условие 6 не выполнится, то производится переход к блоку 4, где при выполнении операции значение переменной увеличивается на 1 и становится равным 2. Теперь алгоритм вновь вернется к блоку 5 и к старому значении суммы добавит новый член 2. После этого сумма станет равной 3. В блоке б вновь проверяется условие получения требуемой суммы и т. д. Цепочка блоков 5-4 будет обрабатываться вновь и вновь до того момента, когда однажды при определенном значении переменной i, наконец, выполнится условие S > К, т. е. когда накапливаемая в таком цикле сумма впервые превысит заданное значение К. Переменная i, значение которой при очередном проходе цепочки этих блоков увеличивается на 1, играет роль счетчика этого цикла. Далее производится переход к блоку 7, где отпечатается значение количества членов ряда (извлечено и отпечатано число из ячейки i, которое там хранится в момент выполнения условия), суммы S и в блоке 8 алгоритм закончит работу. Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N ( под длиной массива понимается количество его элементов ). Блок-схема алгоритма дана на рис. 6.
Вначале в блоке 2 производится ввод двух переменных N и Z. Первая из них представляет одну ячейку. В нее записывается одна константа – число, равное количеству элементов массива Z. Именно такое количество ячеек объединяет другая переменная – Z. Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда самое N еще не известно (оно будет введено позже Z). Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к дальнейшему накоплению необходимой суммы. Блоки 4-6 представляет собой сам цикл, в котором накапливается сумма.
Рис. 6. Циклический алгоритм
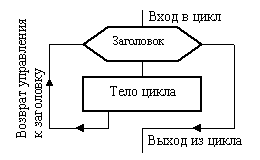
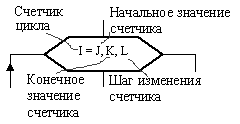
Для того чтобы понять, как функционирует не только этот, а и любой другой цикл, обратимся к рис. 7, 8. На них показана общая структура цикла и его важнейшие параметры. Как видно из рис. 7, цикл состоит из заголовка и тела. Всякий цикл обязательно имеет свой счетчик. На рис. 8, где показана структура и параметры заголовка цикла, роль такого счетчика выполняет переменная i. Внутри заголовка после счетчика и символа "=" через запятую указывает начальное и конечное значения счетчика и шаг его изменения (на рис. 8 их роль выполняют переменные j, k, l соответственно). Если значение шага l = l, то его можно не указывать. Сначала производится вход в цикл. После этого начинается его выполнение.
Рис. 7. Структура цикла Рис. 8. Структура заголовка цикла
Вернемся к блок-схеме рис. 6. Заголовок ее цикла представлен блоком 4. Роль счетчика цикла играет переменная i, которая должна в цикле изменяться от 1 до N. Поскольку шаг явно не указан, то по умолчанию он подразумевается равным 1. Тело цикла образуют блоки 5 и 6. Сразу после входа в цикл переменная i примет начальное значение i = 1. Далее в блоке 5 выполняется проверка положительности первого элемента массива Z (т. к. i = 1). Если этот элемент действительно положителен, то в блоке б он будет добавлен к переменной S, после чего выполняется возврат к заголовку цикла. Если этот элемент не положителен (т. е. нуль или отрицательный), то будет выполнен переход сразу к заголовку цикла, минуя блок суммирования 6. На втором круге цикла счетчик i в заголовке увеличится на 1 и станет равным 2. Теперь, при новом выполнении тела цикла, в блоке 5 проверяется на положительность второй элемент массива Z и, если он положителен, то добавляется в сумму и т. д. Последний раз тело цикла выполнится при i = N. При этом значении счетчика проверяется последний элемент массива. Наконец, в заголовке цикла i примет значение N+1. Это значение выходит за предписанный предел, следовательно, произойдет выход из цикла и управление перейдет блоку 7. В этом блоке выводится накопленная сумма и алгоритм закончит работу. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
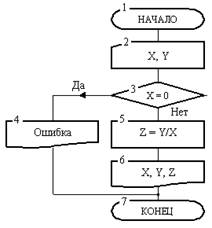 Она состоит из 7 блоков. После начала работы алгоритм в блоке 2 требует ввода аргументов X и Y. Затем в блоке 3 производится проверка условия X = 0. Здесь автомат проверяет равна ли нули константа, введенная в ячейку с адресом X. Результатом такой проверки является ответ "Да" или "Нет". В зависимости от этого ответа выполнение алгоритма пойдет по одной или другой ветви. Если результат проверки окажется отрицательным, то на х можно делить и управление передается блоку 4.
Она состоит из 7 блоков. После начала работы алгоритм в блоке 2 требует ввода аргументов X и Y. Затем в блоке 3 производится проверка условия X = 0. Здесь автомат проверяет равна ли нули константа, введенная в ячейку с адресом X. Результатом такой проверки является ответ "Да" или "Нет". В зависимости от этого ответа выполнение алгоритма пойдет по одной или другой ветви. Если результат проверки окажется отрицательным, то на х можно делить и управление передается блоку 4.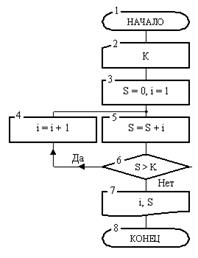 Блок-схема алгоритма решения этой задачи приведена на рис. 5. Она состоит из восьми блоков.
Блок-схема алгоритма решения этой задачи приведена на рис. 5. Она состоит из восьми блоков.