|
|
Социальная деятельность и социальные показатели 12 глава
При исчислении выборочных показателей по выборке необходимо учитывать оба компонента случайной ошибки (как и в случае двухступенчатого отбора), связанного со структурой выборки первой фазы (n) и второй фазы ( Комбинированные выборки. Соединение в многоступенчатой выборке различных приемов отбора (простого случайного, систематического или серийного) делает выборку комбинированной. Как уже указывалось, большинство используемых в современных социологических исследованиях выборок являются комбинированными. Одноступенчатая стратифицированная выборка. Комбинированная одноступенчатая выборка использовалась социологами ИСИ АН СССР при формировании выборочной совокупности для изучения индивидуальной производительности труда (индивидуальных норм выработки) рабочих сдельщиков. Пример. На основе предварительного анализа пилотажного массива из шести возможных для формирования выборки признаков {возраст, образование, стаж по профессии и на данном заводе, заработная плата и квалификация) были выбраны два—заработная плата и стаж по профессии. Эти признаки обнаружили наибольшее влияние на изучаемый показатель — норму выработки[122]. Генеральная совокупность была стратифицирована на 6 страт, различающихся уровнем заработной платы. Отбор в стратах имел случайный характер — по распределению второго по весу признака (стаж по профессии). Были известны следующие данные по генеральной совокупности.
Размер выборки для бесповторного отбора был определен по формуле (см. табл. 16).
где В связи с тем что построение репрезентативной районированной выборки означает сохранение в выборке пропорции для групп генеральной совокупности, для определения размера групп выборочной совокупности принимается следующий план[123]:
Пропорциональнее построение выборки соответствовало следующим необходимым размерам групп:
Следующая стадия работы заключалась в расчете доли для страт стажа. Для пропорционального построения выборки отбор по стажу следует согласовать с планом: где Когда найдены эти доли для каждой страты по стажу, рассчитывается, сколько единиц наблюдения и с каким стажем должно попасть из каждой такой страты в выборочную совокупность. Например, доля для стажа 1 — 2 года и заработной платы 60 — 80 руб. равна 0,60, а для стажа 3 — 4 года в той же типической группе доля равна 0,40. Исходя из них, находим размер выборки для каждой страты:
Аналогичный расчет производится по всем остальным стратам, В результате формируется план пропорциональной выборки в абсолютных числах и процентах (табл. 20). По таблице случайных чисел выбираются случайные числа в соответствии с размером каждой группы, представленной в выборке (табл. 20). Предварительно картотека была стратифицирована по группам заработной платы и карточки пронумерованы. Из каждой группы выбирались карточки, соответствующие случайным числам. Если стаж на выбранной карточке должен был быть представлен в группе, карточка отбиралась в выборку. Если стаж не должен, был быть представлен в данной группе, карточка возвращалась в генеральную совокупность. Появление карточек, которые возвращались в массив, потребовало дополнительного выбора случайных чисел для каждой группы, пока не был обеспечен намеченный по плану размер. Как видно из табл. 20, некоторые смещения оказались в группах с большим стажем. Но выборка репрезентативна по контролируемому признаку — средней норме выработки: в генеральной совокупности—109%, в выборке—108,9%.
Таблица 20.План выборки
Рассчитаем по этой выборке оценку доли перевыполняющих план выработки в генеральной совокупности[124] (табл. 21). Таблица 21. Распределение численности выполняющих план (выборочные данные)
Общая доля рабочих, перевыполняющих план, равна Чтобы использовать показатель доли по выборке как оценку соответствующего параметра в генеральной совокупности, необходимо рассчитать среднюю ошибку выборки. Расчет дисперсии доли в стратифицированной выборке производится по формуле
Расчет средней ошибки выборки производится по формуле
При доверительной вероятности 0,95 предельная ошибка выборки D = ZМ = 1,96 * 0,0084 = 0,016, или 1,6%. Таким образом, с вероятностью 0,95 можно утверждать, что доля перевыполняющих план будет в интервале (81 ± 1,6)%. 6. Неслучайные методы отбора и другие подходы к построению выборки Выборочный метод в условиях недостатка информации о генеральной совокупности. Недостаток информации о генеральной совокупности в той или, иной форме свойствен любому выборочному исследованию (для восполнения недостатка оно и проводится). Будем выделять два типа априорной информации о генеральной: совокупности: а) есть перечень объектов генеральной совокупности и нет сведений о дисперсии изучаемой характеристики, б) нет перечня объектов генеральной совокупности. В случае а) недостаток информации, как это уже отмечалось выше, преодолевается путем проведения одного - двух пробных исследований. Для планирования пробных исследований можно рекомендовать использование таблицы достаточно больших чисел[125]. Один из вариантов таких таблиц задает численность выборки, рассчитанную на основе закона больших чисел безотносительно к объему генеральной совокупности. Если известен коэффициент вариации генеральной совокупности, то объем выборки может быть определен по номограммам достаточно больших чисел. Если генеральная совокупность позволяет найти размах колебания признака, то естественно воспользоваться приближенным расчетом дисперсии с помощью табл. 17. Для расчетов по качественной характеристике проведение пробных исследований не является обязательным, так как можно пользоваться максимально возможным значением дисперсии Случай б) значительно затрудняет использование описанных методов вероятностного отбора в социологических исследованиях. К настоящему времени наметились в социологии две тенденциив их преодолении. Первая связана с применением более сложных схем случайного отбора стратифицированного, многоступенчатого, комбинированного (о чем речь шла в параграфах 4 и 5 настоящей главы). Вторая связана с отказом от строгого выполнения условий вероятностного отбора. В социологии применяется ряд приемов формирования выборочных совокупностей, которые строятся по подобию вероятностных, но для которых нельзя строго обосновать, что выборочные характеристики выступают оценками соответствующих характеристик генеральной совокупности. Такие выборки можно назвать эмпирическими, так как они не имеют теоретического вероятностного обоснования. Стихийная выборка. Широко известна так называемая выборка первого встречного, которая лишь на первый взгляд кажется вероятностной. Социолог в этом случае может бессознательно руководствоваться при выборе лиц для опроса чувством личной симпатии или антипатии, соображениями удобства и т. п. Выборку первого встречного и другие, ей подобные, принято называть не вероятностными, а стихийными. Эти способы организации выборки характеризуются тем, что для них невозможно уточнить, какую генеральную совокупность они представляют. Примером стихийных выборок являются опросы с помощью радио или телеанкет, а также анкет, опубликованных в печати. Генеральной совокупностью каждый раз выступает аудитория, читатели того или иного канала массовой коммуникации. Однако из-за незнания каких-либо характеристик этой генеральной совокупности, а чаще всего и ее размера невозможно определить качество выборки: достаточно хорошо она репрезентирует генеральную совокупность или дает совершенно искаженную картину. Примером стихийного метода формирования выборки может служить процедура, разработанная сотрудниками ИСИ АН СССР для опроса посетителей международной выставки «Связь-81»[126]. Трудность построения выборки заключалась в том, что было невозможно организовать точный, счет посетителей, входящих на территорию и выходящих с территории выставки. Поэтому была предложена компромиссная процедура: несколько интервьюеров, стоящих на каждом входе и выходе выставки, независимо друг от друга начинали вести (со сдвигом во времени) счет посетителей — в выборку отбирался десятый посетитель. Он опрашивался данным интервьюером, и затем этот же интервьюер вновь отбирал десятого посетителя по аналогичной процедуре. Поскольку опрос велся на входе в выходе с выставки, появилась возможность проверить репрезентативность результатов. Сопоставление социально-демографических показателей позволяет говорить о достаточной точности данной процедуры. Квотная выборка. Наиболее распространенной из числа не строго случайных методик формирования выборочной совокупности является квотная выборка. Она строится как модель, воспроизводящая структуру генеральной совокупности в виде квот (пропорций) распределения изучаемых признаков или признаков, с ними взаимосвязанных. Число единиц (элементов выборочной совокупности) с различным сочетанием изучаемых признаков определяется с таким расчетом, чтобы оно соответствовало их доле (пропорции) в генеральной совокупности. Квотная выборка часто применяется в массовых опросах населения и особенно при изучении общественного мнения. На основании квотной выборки устанавливается, сколько лиц и с какими характеристиками следует опросить. Применение квотной выборки в чистом виде возможно при наличии на момент проведения опроса достаточно подробных сведений о генеральной совокупности. Формирование модели генеральной совокупности означает наличие информации о независимом распределении каждого из изучаемых признаков или об их условном распределении. Эта картина с учетом размера, выборки должна быть воспроизведена в модели. Самым сложным моментом является (особенно если необходима всесоюзная модель) географическое соотнесение выборки, т. е. определение, какие конкретно населенные пункты включать в выборку. Непосредственная реализация квотной выборки соответствует организации опроса лиц согласно квотам. Существует два способа задания квот: 1) интервьюеру дается обязательный набор признаков, которым должен обладать каждый респондент, и указывается общее число респондентов, подлежащих опросу; 2) задание ограничивается перечислением независимых характеристик контингента, подлежащего опросу в определенном населенном пункте. Первый способ был использован советскими социологами в исследовании городских кинозрителей[127]. Например, задание для интервьюера, направленного в Магнитогорск, предполагало учитывать при опросе следующие признаки респондентов (табл. 22). Таблица 22
При втором способе это задание выглядело бы так: опросить 6 человек со следующими свободными параметрами:
Формирование модели для квотной выборки полностью соответствует условиям вероятностного отбора. Отличие квотной выборки начинается со способа отбора респондентов, который содержит опасность систематических смещений. При выборе лиц для опроса интервьюеры на практике часто совершают ошибки Типа выбор себе подобных. В роли интервьюеров нередко выступают студенты, молодежь, неосознанно отдающие предпочтение тем, с кем им легче общаться. Поэтому в квотных выборках часто наблюдается завышение доли лиц с высшим образованием и более молодых возрастных групп. По некоторым литературным данным, при условии соблюдения оптимального объема квотной выборки ее точность конкурирует с точностью случайных выборок и даже может превышать последнюю[128]. Однако отсутствие теоретических гарантий точности выводов, полученных с помощью квотной выборки, снижает ее ценность. В связи с этим основное достоинство выборки состоит в простоте ее реализации, быстроте проведения. Другие сложности и проблемы построения выборки. Если исследуется генеральная совокупность по качественному признаку, имеющему всего лишь две градации (да — нет; имею — не имею и т. п.), то возможно применение вышеизложенного аппарата статистических оценок. Но если качественный признак имеет несколько градаций или вообще не разработана его классификация? В первом случае необходимо предварительно укрупнить имеющиеся градации, сведя их к двум более широким классам. Например, если исследуется признак с тремя градациями: не выполнившие план, выполнившие план и перевыполнившие план, то информация собирается по признаку, измеренному по дихотомической шкале, скажем, в виде: не выполнившие план — одна градация и выполнившие и перевыполнившие план — другая. Значительно сложнее обстоит дело, если качественный признак оказывается даже не измеренным по номинальной шкале. Например, как применить выборочный метод для исследования образа жизни, общепринятой типологии которого пока еще нет? Выборку для исследования подобного вопроса нельзя организовать, не имея некоторых показателей, так или иначе связанных с исследуемой качественной характеристикой. Иногда удается решить вопрос об использовании определенного показателя для организации выборки по качественному признаку путем разработки соответствующих исследовательских гипотез. Например, при исследовании киноаудитории социолог может выдвинуть гипотезу о зависимости вкусов и предпочтений кинозрителя от его образования. Тогда, зная, что в исследуемой генеральной совокупности 15% лиц с высшим образованием, 40% со средним и 45% с неполным средним он должен выдержать эти пропорции в выборке. Если исследовательская гипотеза предполагает также, что вкусы кинозрителя зависят в среднем от его возраста, то в выборке должны быть пропорционально представлены те возрастные группы генеральной совокупности, которые интересуют исследователя. Однако сравнительно редко удается ограничиться двумя - тремя показателями для адекватного представления качественной характеристики. Значительно чаще, прежде чем приступить к использованию выборочного метода (так же как и любого другого статистического наблюдения), необходимо разработать систему показателей, отражающих качественную характеристику. Построение системы показателей — сложнейший с методической точки зрения этап всего социологического исследования. Сложность усугубляется отсутствием каких бы то ни было формальных критериев для отбора показателей в систему, отражающую данную качественную характеристику. Вопрос в каждом случае решается на основании тщательного содержательного рассмотрения проблемы социологического исследования. Но трудности не заканчиваются с построением системы социальных показателей для исследуемой качественной характеристики. Возникает вопрос о построении выборочной совокупности по разработанной системе показателей. Если количество показателей системы невелико, то в принципе возможно последовательное применение изложенного аппарата выборочного метода для одной переменной. Однако этот путь требует значительных усилий, так как приходится по-новому организовывать выборочную совокупность при переходе от одного показателя к другому. Перспективным оказывается принципиально другой подход при планировании выборочной совокупности, основанный на применении всей разработанной системы показателей одновременно. Особенно эффективным он оказывается, когда число показателей системы велико. А именно этот случай весьма характерен для многих социологических исследований. Описываемый подход реализуется в социологических исследованиях с помощью того или иного метода многомерного анализа эмпирических данных. Его сущность состоит в предварительной стратификации всей генеральной совокупности по всей системе показателей. Здесь приобретают важное значение различные методы автоматической классификации, например таксономия, метод структурной классификации, а также причинный анализ и методы многомерной статистики[129]. Организацию выборочного исследования с применением методов многомерного анализа социологу целесообразно проводить в тесном контакте со специалистом по многомерной статистике. Все усилия, затраченные социологом при подготовительной работе при организации выборочной совокупности по системе показателей с помощью многомерных методов, окупятся на стадии сбора социологической информации по рассчитанной таким образом выборке и анализу их результатов. Литература для дополнительного чтения
ГЛАВА СЕДЬМАЯ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
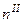= 400
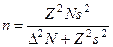
m — выборочная доля. Дисперсия качественного признака (выполнение нормы сдельщиками) при отсутствии информации была принята равной 
= 0,5*0,5 = 0,25. Доверительная вероятность 1 — a = 0,95; предельная ошибка репрезентативности D = 0,05.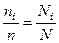
, где N и п — размеры соответственно генеральной совокупности и выборк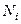и; 
и 
— размеры соответственно страт в генеральной и выборочной совокупностях. Рассчитывается численность каждой страты (представительство групп заработной платы) в выборке
.
, 
, 
, 
, 
,
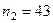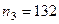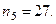
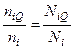— численность каждой страты по стажу в отдельной страте по уровню зарплаты в генеральной совокупности,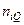 
— соответственно для выборки.
и 
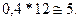
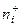
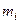
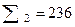
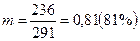
(11)
; 
;
; 
;
; 
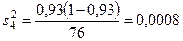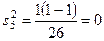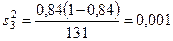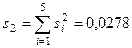, или 2,78%.
(12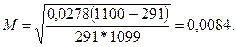
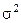= 0,25, получаемой при равной доле наличия и отсутствия исследуемого признака. В таком случае планируемый объем выборки оказывается несколько завышенным для выбранного уровня доверительной вероятности.