|
|
Социальная деятельность и социальные показатели 11 главаТеперь можно определить величину предельной ошибки (см. табл. 16):
Таким образом, доверительные границы для доли неинформированных в генеральной совокупности равны 0,02 ± 0,009, или от 1,1 до 2,9%. Приведем иллюстративный пример определения объема простой повторной случайной выборки. Как видно из формул, чтобы определить объем (см. табл. 16), дл его оценки необходимо знать дисперсии генеральной средней или хотя бы ее оценки. Для применения соответствующей формулы необходимо оцепить значение дисперсии, что можно сделать (при отсутствии информации о ней и о размахе значений признака в генеральной совокупности) путем проведения одной - двух пилотажных (пробных) выборок. Допустим, что в результате пилотажа выборочная оценка дисперсии равна 12,24. Определим, каким должен быть объем выборки, чтобы с вероятностью 0,95 предельное отклонение выборочной средней от генеральной не превышало одного экземпляра газет. При этих условиях получаем численность планируемой выборки
Таким образом, объем выборки должен составлять 24 человека. 3. Систематическая и серийная выборки Систематический отбор. В Социологических исследованиях иногда применяется несколько упрощенный вариант простого случайного отбора, который носит название систематического. Основа выборки для него характеризуется теми же требованиями, что и для Простого случайного отбора. Иными словами, основу выборки составляют различные алфавитные списки, картотеки учреждений, домовые книги и т. п. При систематическом отборе выбор единиц наблюдения осуществляется через один и тот же интервал k из исходного списка. Например, при k = 20 выбирается 3, 23, 43, 63 и т. д. единиц списка. Таким образом, элементы выборочной совокупности однозначно определяются при систематическом отборе номером первого элемента (тройки в нашем примере) и величиной интервала . В одной из схем систематического отбора в качестве первого элемента выбирается средний элемент списка или стоящий рядом с ним. Так, если список генеральной совокупности пронумерован от 1 до N, то номер первого элемента может быть определен по формулам Более распространен выбор первой единицы отбора случайным образом (например, по таблице случайных чисел). Величина А зависит от характера поставленной проблемы, от разброса значений исследуемой характеристики генеральной совокупности. Если решен вопрос об объеме планируемой выборки, то число определяется в зависимости от объема генеральной совокупности и объема выборки (n). Если N — кратное числа n, то интервал определяется по формуле если если Здесь [ ] означает целую часть числа. Поясним сказанное на примере: пусть N = 19 и n = 5, чему равно k? Тогда k равно либо 3, либо 4. При k = 3 в выборку попадает больше пяти элементов в данном случае 6 или 7. При k = 4 в выборку попадут пять или четыре элемента. Расчет характеристик систематической выборки. В связи с тем что систематическая выборка определяется как разновидность простого случайного отбора, ее характеристики рассчитываются с помощью соответствующих формул табл. 16. В примере с подписчиками газет и журналов (см. табл. ,15) в систематическую выборку объемом 5 единиц попали номера респондентов 10, 20, 30, 40, 50, для которых соответствующее число выписываемых газет равно 3, 5, 5, 3, 2. Среднее по выборке равно 3,6, а дисперсия — 1,44 ( = 1,2). Применяя для простоты формулы повторной случайной выборки, получаем Таким образом, с вероятностью 0,95 можно утверждать, что доверительный интервал для генеральной средней имеет следующие границы: (3,6 ± 1,96 0,54) = (3,6 ± 1,05) = (2,55; 4,65). Возможности и ограничения систематической выборки. Систематическая выборка является экономными удобным способом формирования выборочной совокупности. Однако при ее применении в социологических исследованиях необходимо следить за тем, чтобы; список, используемый в качестве основы выборки, не обладал порядком, отражающим периодичность в значениях изучаемой характеристики. Проиллюстрируем это положение. При составлении основы выборки для опроса рабочих в одном из цехов завода выбранный интервал может совпасть с числом рабочих в бригаде, в списке которой первым окажется бригадир. При систематическом отборе повышаются шансы попадания в выборку только одних бригадиров. При такой реализации выборки повышается вероятность получения значительных систематических ошибок. Предварительное расположение элементов генеральной совокупности по убыванию или возрастанию исследуемой характеристики позволит избавиться от этой опасности. Так, если в рассмотренном примере основа выборки организуется на базе платежной ведомости, в которой лица расположены в порядке возрастания их заработной платы, то опасность попадания только на одних бригадиров исключается. Систематическая выборка из-за простоты реализации получила широкое применение в социологических исследованиях. Серийная (гнездовая) выборка. При серийной выборке единицы отбора представляют собой статистические серии, т. е. совокупности статистически различимых единиц. В качестве таких единиц могут выступать семья, бригада, школьный класс, небольшие производственные коллективы в учреждениях, почтовые отделения, врачебные участки, населенные пункты, территориальные общности и т. п. Отобранные в выборку серии подвергаются сплошному или выборочному обследованию. Второй вариант используется в практике социологических исследований гораздо чаще, чем первый. Собственно говоря, любая многоступенчатая выборка представляет собой гнездовую выборку, в которой единицы отбора на высших ступенях являются гнездами из единиц отбора нижних ступеней. Организация серийной выборки. Серийная выборка имеет существенные организационные преимущества перед простой случайной выборкой, так как значительно легче произвести отбор и изучение нескольких коллективов, бригад, цехов и т. д., находящихся на одном месте, чем нескольких сотен пространственно разбросанных людей. Процедура отбора позволяет сконцентрировать выборку в сравнительно небольшом числе пунктов. Серийная выборка может организовываться по схемам простой случайной и систематической выборок. Наконец, она может формироваться после предварительного районирования генеральной совокупности. В первых двух случаях к информации о генеральной совокупности — основе выборки — предъявляются те же требования, что и ко всем вероятностным выборкам: размещение элементов генеральной совокупности (серий) не должно быть каким-либо образом систематизировано. Метод маршрутного опроса. Этот метод социологи часто используют, когда единицей наблюдения выступает семья. В выборочную совокупность, например, намечено включить определенное число случайно отобранных семей или квартир. На карте города или населенного пункта нумеруются все улицы. С помощью таблицы случайных чисел отбираются большие числа, которые позволяют идентифицировать семьи или квартиры, попавшие в выборку. Каждое большое число рассматривается как состоящее из трех компонентов: первые две или три цифры в нем указывают номер улицы, следующая цифра — номер дома, последняя цифра — номер квартиры в выбранном доме. Например, число 42—25—3 указывает квартиру № 3 дома № 25 на 42-й улице. Организация серийной выборки методом маршрутного опроса наиболее приспособлена к городам, где преобладают отдельные квартиры, или к населенным пунктам, где еще сохраняется частное домовладение (в последнем случае отпадает необходимость выбирать номер квартиры). Возможности и ограничения серийной выборки. При серийной выборке всегда имеет место занижение по сравнению с генеральной совокупностью дисперсии изучаемого признака в силу определенного сходства единиц в сериях. Например, вполне объяснима заметная связь между членами семьи. Характер профессий детей в определенной мере может зависеть от профессии родителей. Очевидна связь членов семьи в отношении их социальной принадлежности. С точки зрения статистика, сходство элементов серий приводит к избыточности однотипной, повторяющейся информации. Социолог должен учитывать этот органически присущий серийной выборке статистический порок при прочих равных условиях, выбирая в качестве гнезд такие общности, которые содержат максимально разнородные конечные единицы наблюдения. Так, при изучении, скажем, качества медицинского обслуживания населения города разумно в виде гнезд выбрать совокупность жителей, обслуживаемых отдельными почтовыми отделениями, или проживающих на территории отдельных ЖЭКов, но никак не врачебные участки, поскольку последний выбор привел бы к искажению результатов. Расчет характеристик серийной выборки. Расчет характеристик серийной выборки имеет некоторое отличие от простой случайной и систематической выборок. Это отличие связано прежде всего с вычислением дисперсий и ошибки выборки. Вычисление средней ошибки серийной выборки основано на дисперсии серийных средних. Пример. Из генеральной совокупности, включающей 16 семей, сделана серийная выборка, состоящая из четырех семей (в каждой семье по 4 человека)[118]. Перед исследователями стоит задача найти оценку средней заработной платы в генеральной совокупности, оценку ее дисперсии и среднюю ошибку выборки (табл. 18). Средняя ошибка бесповторной серийной выборки определяется по формуле
где
Таблица 18.Данные для примера
Расчет дисперсии серийных средних:
Тогда
В зависимости от выбранной доверительной вероятности средняя заработная плата для генеральной совокупности 83,5 ±Z1,53. Например, исследователь может с вероятностью в 0,95 утверждать, что в данной генеральной совокупности средняя заработная плата не меньше 80,6 руб. и не больше 86,5 руб. Так как вычисление ошибки для серийной выборки основано на дисперсии серийных средних, то серийный отбор будет тем репрезентативнее, чем меньше степень колеблемости серийных средних, измеряемая величиной их дисперсии. 4. Стратифицированный отбор Понятие стратифицированной выборки. Вероятностная выборка с любой техникой отбора (простая случайная, систематическая, серийная или многоступенчатая) становится стратифицированной, если процедурам отбора предшествует выделение в генеральной совокупности однородных частей, называемых стратами. В статистическом смысле стратификация соответствует выделению таких статистически однородных групп, колеблемость изучаемых признаков которых внутри меньше, чем между ними. Эта дифференциация внутри генеральной совокупности на качественно более однородные группы содержательно связана с предметом исследования. Стратификация совокупности оказывается необходимой во всех случаях, когда совокупность является неоднородной по социальным, экономическим и другим характеристикам единиц наблюдения. Так, исследуя профессиональную ориентацию школьников в пределах одного города, можно в одну страту отнести 16 школ, расположенных в районе старых застроек, во вторую — 20 школ, расположенных в районах новостроек. Для опроса можно отобрать выпускников из двух школ первой страты, а также из двух школ второй страты. Если такая группировка школ действительно отражает различия районов, которые существенно учитывать в исследовании профессиональной структуры, то колеблемость изучаемых признаков внутри каждой группы школ должна быть меньше, чем между группами. В качестве страт могут быть использованы как естественные образования, так и специально формируемые для определенного исследования. Например, такими стратами могут выступать экономико-географические регионы или области страны, города, классифицированные по их административному статусу и по численности населения. Стратами могут выступать и идеальные образования. Примером является выделение в генеральной совокупности при исследовании отношения молодежи к труду, шести групп по содержанию труда[119]. Стратифицирующий признак. Признак, по значениям которого производится стратификация генеральной совокупности, называется признаком стратификации. Стратификация может проводиться по одному или нескольким признакам. Организация стратифицированной выборки. Организация стратифицированной выборки требует представления о характере распределения по всей совокупности тех признаков, которые должны быть положены в основу образования типических групп, или страт. Неправильный выбор признака для группировки элементов генеральной совокупности может не увеличить репрезентативность выборочных данных по сравнению со случайной выборкой того же объема. Организация стратифицированной репрезентативной выборки связана на практике с известными трудностями, особенно если выделенные страты неравночисленны Математическая статистика рекомендует в этих случаях, чтобы размеры выборки из каждой страты были пропорциональны средним квадратическим отклонениям в соответствующих стратах генеральной совокупности. Но дисперсии, как правило, неизвестны. Поэтому часто при организации отбора из страт генеральной совокупности производится отбор пропорционально их размеру (доле) в общей численности совокупности. Еще один употребляемый в социологии вариант выбора — это отбор одинакового количества единиц наблюдения из неравных типических групп. Выборка организуется в зависимости от рассмотренных вариантов отбора с объемом, который рассчитывается по следующим формулам. 1. Пропорционально среднеквадратическому отклонению 5; в 1-й типической группе, найденному по результатам пробного исследования. Размер (
где п — объем всей выборки;
2. Пропорционально размеру групп: 3. Отбор равного числа единиц наблюдения Расчет характеристик стратифицированной выборки. Характеристики такой выборки рассчитываются как взвешенные величины: показатели по каждой страте комбинируются в общую среднюю; вклад групповых средних пропорционален весу каждой страты в выборочной или генеральной совокупности. В стратифицированной выборке общая дисперсия выборки имеет как бы два источника: дисперсию групповых средних, которые характеризуют каждую страту Это записывается следующим образом:
Расчет средней ошибки при отборе, пропорциональном численности единиц в стратах, производится по формуле
или, если пренебречь отношением n/N,
В выражениях (8) и (9)
Таблица 19.Данные к примеру
Из соотношения для средней ошибки (7) следует, что ошибка стратифицированной выборки меньше средней ошибки чисто случайной выборки либо равна ей, когда межгрупповая дисперсия равна нулю. Пример. Предположим, что выборка содержит 5 страт (группы семей по среднему доходу[120]). Необходимо определить величину расходов на годовую подписку. Из каждой i-й страты взяты по две семьи (объем выборки п = 10, см. табл. 19), Расчет:
Найдем дисперсию, не учитывая расслоение семей на 5 групп:
Отсюда внутригрупповая дисперсия Для случайной выборки Таким образом, как видно из рассмотренного примера, стратифицированная выборка при прочих равных условиях дает более точные результаты. 5. Многоступенчатые и комбинированные способы формирования выборочной совокупности Выборка может строиться как одно- или многоступенчатая. При многоступенчатом отборе на каждой ступени меняется единица отбора. Например, на первой ступени производится отбор промышленных предприятий, на второй — отбор бригад на предприятиях, попавших в выборку па первой ступени, на третьей — отбор рабочих из бригад, попавших в выборку на второй ступени, отбора, и т. д. Необходимость многоступенчатого отбора вызвана, как правило, отсутствием информации о всех единицах генеральной совокупности. При многоступенчатом отборе для организации первой ступени необходимо иметь информацию о распределении того или иного признака по всей совокупности единиц отбора первой ступени. Для организации второй ступени нужна уже только информация об отобранных единицах первой ступени. На первой ступени, как правило, используется случайный отбора начиная со второй ступени случайно отбирается количество единиц, пропорциональное размеру соответствующей единицы предыдущей ступени и т. д. Доли отбора на каждой ступени комбинируются таким образом, чтобы в целом доля отбора выборки обеспечивала всем единицам генеральной совокупности равные шансы попасть в выборку. Пропорциональный способ организации многоступенчатой выборки имеет определенные неудобства. Социолог, с одной стороны, уменьшает объем выборки в целях экономии средств и сокращения сроков проведения исследования, а с другой, — соблюдая принцип пропорциональности, он может получить очень малочисленные группировки по отдельным факторам, которые окажутся недостаточными для статистического анализа. Существует несколько способов формирования многоступенчатых выборок. Для примера рассмотрим способ организации двухступенчатой выборки, отбор единиц которой на первой ступени осуществляется с вероятностью, пропорциональной размеру. Воспользуемся для примера условиями и задачами организации выборки в известном исследовании ленинградских социологов. Единицы первой ступени отбора — предприятия города. Составляется полный список единиц наблюдений первой ступени отбора — промышленных предприятий и численности молодых рабочих па каждом из них. Генеральная совокупность включала 50 таких предприятий.
Единицы отбора ранжируются по численности рабочих, выделенных в качестве единиц наблюдения. Принимается решение о включении в выборку определенного числа заводов, например пяти. По таблице случайных чисел выбирается 5 чисел ( Вторая ступень отбора реализуется, следующим образом. На каждом предприятии, включенном в выборку, выбирается одно и то же число рабочих ( Ошибка многоступенчатой выборки (на примере двухступенчатой выборки). При многоступенчатом отборе (начиная с двухступенчатого) следует учитывать специфику расчета ошибки выборки. Каждая ступень отбора делает свой вклад в отклонение находимых оценок от истинных значений характеристик в генеральной совокупности. Для достаточно большого объема выборки существуют упрощенные формулы расчета средней ошибки. Для двухступенчатой выборки
где В формуле учтены оба источника ошибок репрезентативности при двухступенчатом отборе. Первый член формулы под корнем указывает па дисперсию, вызванную формированием первой ступени отбора. Второй член указывает па внутригрупповую дисперсию, связанную с организацией второй ступени выборки. Упрощенность этой формулы состоит в том, что внутригрупповые дисперсии рассчитываются внутри каждой единицы первой ступени после отбора из нее единиц второй ступени. Здесь указана «невзвешенная» средняя из квадратов ошибок по всей сумме единиц второй ступени ( Многофазовый отбор. Многофазовый отбор является особым видом многоступенчатого отбора. Он заключается в том, что из сформированной выборки большего объема производится новая выборка (подвыборка) меньшего объема и т. д. Особенностью этого способа формирования выборочной совокупности является то, что независимо от числа фаз в последующих подвыборках используется неизменно одна и та же единица отбора, что и в основной выборке. К многофазовому отбору прибегают тогда, когда в рамках исследования, которое проводится на большой выборке, возникает необходимость тщательного изучения более узкого круга вопросов. Для этих целей формируется вторая фаза — та же выборка в миниатюре и т. д. Как и в многоступенчатых выборках, при многофазовом отборе каждая фаза является источником случайных ошибок. Пример двухфазовой стратифицированной выборки[121]. В ходе, исследования сельского населения возникла необходимость более углубленно изучить его культурные потребности и материальные затраты на потребление культуры. Основная выборка (п) была сделана из стратифицированной генеральной совокупности — изучаемый регион был разделен на 5 трат по типу хозяйств: от мелких (1) до самых крупных (5). Вторая фаза выборки ( 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
или 0,9%
.
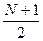, если N — нечетное и N/2, если N — четное число.
. Если N некратно n, то реальный объем выборки 
и планируемый объем 
при различных способах вычисления числа k связаны следующими соотношениями:
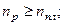
, то 
, то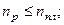 
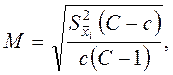
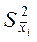— дисперсия серийных средних; С — число серий в генеральной совокупности (равных по численности); с — число серий в выборке.
, руб.
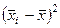
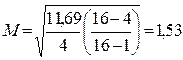
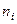) выборки из i-й типической группы равен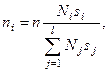
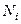— объем i-й группы в генеральной совокупности; l — количество групп. Весь объ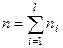ем выборки равен
, где N объем генеральной совокупности. Весь объем выборки равен 
. Весь объем выборки определяется по формуле 
.
, и среднюю дисперсию из дисперсий внутри каждой из этих страт 
. Первую составляющую принято называть межгрупповой дисперсией, а вторую — внутригрупповой дисперсией.
(7)
(8)
(9)
, где 
— общая дисперсия выборки — подсчитывается как для простой выборки, не принимая во внимание стратификацию.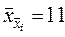
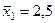
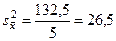
= 11
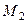, ошибка для стратифицированной выборки 
.
.
, 
, 
, 
и 
) между N1 и N (общей кумулированной численностью рабочих в генеральной совокупности); В выборку включаются те предприятия, чьи номера (i) оказались в той же строке (j), которая соответствует кумуляте, содержащей одно из чисел 
(k = 1¸5), т. е. i = j, если N1 + N2 + ... + Nj-1< 
единиц второй ступени отбора). Далее отбор может быть случайным или систематическим.
(10)
— дисперсия единиц первой ступени отбора и п1 — их численность; 
—дисперсия единиц второй ступени отбора и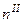 
— их численность в составе единиц первой ступени отбора в выборке.