
|
|
Экономико-математическое моделированиеЭкономико-математическое моделирование в настоящее время один из инструментов экономического анализа. Использование экономико-математических методов и моделей позволяет получить новые качественные выводы об социально-экономических процессах и явлениях, изучить общие тенденции их развития.Это можно осуществлять, применяя специальные методы прогнозирования. В зависимости от формы модели для анализа и прогноза используются различные подходы, алгоритмы, критерии. Существует много методов прогнозирования, среди которых можно выделить метод анализа временных рядов. Он основан на допущении, согласно которому случившееся в прошлом дает достаточно хорошее приближение в оценке будущего. При изучении в рядах динамики основной тенденции развития (тренда) решаются две взаимосвязанные задачи: · выявление в изучаемом явлении наличия тренда с описанием его качественных особенностей; · измерение выявленного тренда, то есть получение обобщающей количественной оценки основной тенденции развития. На практике наиболее распространенными методами статистического изучения тренда являются: укрупнение интервалов, сглаживание скользящей средней, аналитическое выравнивание. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития Yt рассчитывается как функция времени: Yti = f(ti) Определение теоретических уровней Yt производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда динамики. Важнейшей проблемой при применении метода аналитического выравнивания является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности решения этой проблемы зависят выводы о закономерностях тренда изучаемых явлений. На практике статистического изучения тренда различают следующие типы развития социально-экономических явлений во времени: 1. Равномерное развитие. Для этого типа динамики присущи постоянные абсолютные приросты: Yt = Cоnst Основная тенденция развития в рядах динамики со стабильными абсолютными приростами отображается уравнением прямолинейной функции: Yt = а + bt, где а и b – параметры уравнения; t – обозначение времени. 2. Равноускоренное (равнозамедленное) развитие. Этому типу динамики свойственно постоянное во времени увеличение (замедление) развития. Уровни таких рядов динамики изменяются с постоянными темпами прироста: Тпр = const Основная тенденция развития в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка: Y = а + bt + сt2 Значение параметров а и b идентичны параметрам, используемым в предыдущей функции. Параметр с характеризует постоянное изменение интенсивности развития (в единицу времени). 3. Развитие с переменным ускорением. Для этого типа динамики основная тенденция развития выражается функцией параболы третьего порядка: Yt = a + bt + ct2 + dt3 В данном уравнении параметр d отображает изменение ускорения. 4. Развитие по экспоненте. Этот тип динамики характеризует стабильные темпы роста: Тр= const Основная тенденция в рядах динамики с постоянными темпами роста отображается показательной функцией: Yt = ab, где а – темп роста (снижения) изучаемого явления в единицу времени.
Основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией: Yt = а + blgt На практике целесообразно выбор функции осуществлять либо на основе анализа аналитических показателей ряда динамики, либо методом перебора ряда функций и выбора той, которой соответствует наименьшая средняя квадратическая ошибка и средняя ошибка аппроксимации. Этапы моделирования: 1. Исходные и расчетные данные о динамике уровня ряда (объем выпуска продукции или оказания услуг, балансовая прибыль, выручка, численность работающих и т.д. за 8-10 лет) заносятся в таблицу. Для наглядного отображения зависимости строят график динамики уровня ряда. По виду графика принимается гипотеза, например, что модель описывается линейной зависимостью: Y=a+bx 3. Определяют параметры модели методом наименьших квадратов МНК, т.е. min Σеi2. Способ наименьших квадратов дает систему двух нормальных уравнений. Система нормальных уравнений:
aåх + båх2 = åух aхср + bxср2 = усрхср уi – фактические уровни из таблицы; n – число членов ряда; х – показатель времени (года, кварталы, месяцы и т.д.), который обозначается порядковыми номерами, начиная от низшего, например:
у^ - оценочные значения полученные из модели; Коэффициенты регрессии: b^ = усрхср – уср * хср / xср2 * xср2 a^ = уср – bхср Особое значение имеет знак перед коэффициентом регрессии. Если перед b^ знак плюс, то с увеличением Х значение У возрастает. Если перед b^ знак минус, то с увеличением Х значение У уменьшается. 3. Оценка адекватности выбранного уравнения тренда: Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии и корреляции.. Коэффициент корреляции: rxy = усрхср – хср * уср / sх * sу Значение парных коэффициентов корреляции свидетельствует о сильной связи между отклонениями фактических уровней сравниваемых рядов от соответствующих им выравненных уровней, если rxy > 0,7. Гипотеза о линейности верна с доверительной вероятностью р=0,95. Если коэффициент корреляции меньше 0,7, то гипотеза о линейности не подтверждается. Значимость коэффициентов регрессии a^ и b^ и парных коэффициентов корреляции rxy проверяется на основе t – критерия Стьюдента: tb = b / mb; ta = a / ma ; tr = rxy / mrxy Случайные ошибки аппроксимации a, b и rxy: mb = Öå(yi – yx^)2 / (n-2) / å(хi – xi ср)2 ma = Öå(yi – y^)2 * åхi2 / (n-2) * nå(хi – xi ср)2 mr xy = Ö1 – rxy2 / (n-2) Если все расчетные значения t- критерия больше tкр.- табличного, это свидетельствует о значимости коэффициентов регрессии и корреляции. Гипотеза о линейности верна. Табличные данные t- критерия Стьюдента
Коэффициент детерминации: R2 = å(yi^x – уср)2 / = å(yi – у)2 показывает, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель. Изменяется в пределах от 0 до 1 и по определению положителен. Если коэффициент детерминации больше 0,9, то модель описывает наиболее существенные стороны рассматриваемого процесса. Проверка адекватности всей модели, в т.ч. и значимости коэффициента детерминации, осуществляется с помощью расчета F–критерия и величины средней ошибки аппроксимации. Значимость уравнения регрессии на основе F–критерия Фишера-Снедекора. Критерий Снедекора: Fф = rxy2 * (n – 2) / (1 – rxy2) . Если все расчетные значения F - критерия больше Fкр.- табличного, это свидетельствует о значимости уравнения регрессии и подтверждает гипотезу о линейности. Моделью можно пользоваться. Табличные данные F- распределения при вероятности α = 0,05
γ -число степеней свободы, количество наблюдений в выборке минус число уровней связи, n –1.
Доверительные интервалы a и b - это проекция подынтегральной кривой, равной доверительной вероятности, решение интегрального уравнения. Интервал зависит от числа степеней свободы (m), доверительной вероятности (р) и разброса случайной величины. При m → ∞ имеет место нормальный закон распредления. Предельные ошибки a, b и rxy: Δa = tнаб * ma; Δb = tнаб * mb; Δr = tтабл * mr Значение средней ошибки аппроксимации не должно превышать 12-15%. Доверительные интервалы для определенных параметров: La min = a – Δa; La max = a + Δa; Lb min = b – Δb; Lb max = b + Δb 4. Прогнозирование динамики на основе метода экстраполяции. Прогнозное значение Yp : Yp = a^ + b^xp определяется на основе экстраполяции линейной зависимости Средняя квадратическая ошибка прогноза: my^p = sост Ö1 + 1/n + (хp – хср)2 / å(хi – хср)2, где хp – прогнозное значение, подставляемое вместо xi sост = Öå(y – y^)2 / n – 1 Доверительный интервал L – диапазон прогноза: Lymin = y^p – Δy^p ;Lymax = y^p + Δy^p; Δy^p = tтабл * my^p Пример: Проанализировать динамику и определить перспективную выручку организации. Исходные и расчетные данные для определения параметров системы уравнения представлены в табл.18. Таблица 18 Исходные и расчетные данные для определения параметров системы уравнения
продолж.табл. 18
Расчёты производятся при помощи табличного редактора Excel по приведённым формулам. Полученные результаты и коэффициенты: Xср = 6; Yср = 15586.27273; (X*Y)ср = 124551.5455 Коэффициенты регрессии: β = 3103,4 α = -3034.1 Уравнение регрессии: У = -3034,1 + 3103,4* Х Среднеквадратические отклонения: dx = 3,1623; dy = 9937,49; dо = 1486,43 Коэффициент корреляции: Kxy = 0,9876. Гипотеза о линейности модели верна, т.к. коэффициент корреляции больше 0,7 и равен 0,9876 Коэффициенты регрессии достаточно значимы, т.к. Оценка значимости коэффициентов по t-критерию Стьюдента: ta = - 2, 855 tb = 19,81 ; tr = 18,349 ta > tтабл. (2,855 > 2,26), tb > tтабл. (19,81 > 2,26) и tr > tтабл. (18,349 > 2,26). Модель линейная – надежна т.е. пригодна для практического применения. Коэффициент детерминации: r2= 0,958 . Коэффициент детерминации больше 0,9, то модель описывает наиболее существенные стороны рассматриваемого процесса. Критерий Фишера-Снедекора: Fф = 8,777 > Fтабл.= 6,94. Модель надежна и может быть использована для практического применения. Случайные ошибки a, b и rxy: mb = 156,684; ma = 1062,682 mkxy = 0,05243 Средняя квадратическая ошибка прогноза myp = 1770,16, при хр = 12 Предельные ошибки a, b и rxy: DA = 2403,788; DB = 354,4191 Доверительные интервалы для определенных параметров: Lamin = -5437,86; Lbmin = 2748,972; Lamax = -630,285; Lbmax = 3457,81 Прогнозное значение Yp Yp12 = 34206,2; Yp13 = 37310.01; Yp14 = 40413,14; Yp15 = 43516.79; Yp16 = 46620,18 На рис. 24 построены графики фактической и расчетной выручки от реализации продукции с прогнозом ее на конец 2003 года и 2004 гг.
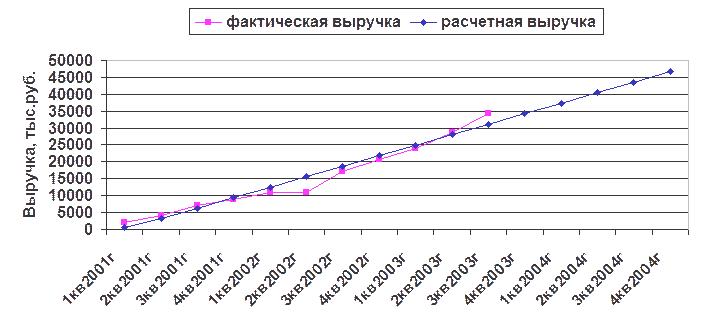 Рис. 24. Динамика выручки от реализации продукции Рис. 24. Динамика выручки от реализации продукции

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 5. Развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики: Yц 0
5. Развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики: Yц 0
 na + båх = åx или a + bxср = хср
na + båх = åx или a + bxср = хср