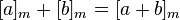Индукционное предположение
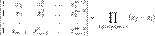
Индукционный переход
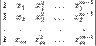
Вычтем из последнего столбца предпоследний, уможенный на 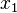 , из , из  -го — -го —  -й, уможенный на -й, уможенный на 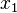 , из , из  -го — -го —  -й, уможенный на -й, уможенный на 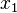 и так далее для всех стобцов. Эти преобразования не меняют определитель матрицы. Получим и так далее для всех стобцов. Эти преобразования не меняют определитель матрицы. Получим

Раскладывая этот определитель по элементам первой строки, получаем, что он равен следующему определителю:

Для всех  от 1 до от 1 до  вынесем из вынесем из  -й строки множитель -й строки множитель  . Получим . Получим
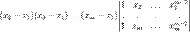
Подставим значение имеющегося в предыдущей формуле определителя, известного из индукционного предположения:
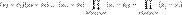
41)Правило крамера
Система линейных уравнений с вещественными коэффициентами:
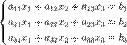
Определители:
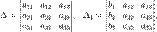
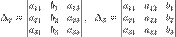
В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы.
Решение:
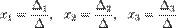
8)Сравнение в кольце целых чисел
Сравне́ние по мо́дулю натурального числа  показывает, что два выбранных целых числа при делении на показывает, что два выбранных целых числа при делении на  дают один и тот же остаток. Целое число может иметь не больше, чем дают один и тот же остаток. Целое число может иметь не больше, чем  остатков; это значит, что все целые числа можно разделить на остатков; это значит, что все целые числа можно разделить на  групп относительно групп относительно  , каждая из которых отвечает определённому остатку от деления на , каждая из которых отвечает определённому остатку от деления на  . .
Сравнимость чисел  и и  записывается в виде формулы (сравнения): записывается в виде формулы (сравнения):
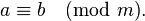
Число  называется модулем сравнения. называется модулем сравнения.
Определение сравнимости чисел  и и  по модулю по модулю  равносильно любому из следующих утверждений: равносильно любому из следующих утверждений:
1. Разность чисел  и и  делится на делится на  без остатка; без остатка;
2. Число  может быть представлено в виде может быть представлено в виде  , где , где  — некоторое целое число[7]. — некоторое целое число[7].
Например, 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4: 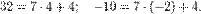
9) свойства сравнений
Для фиксированного натурального числа  отношение сравнимости по модулю отношение сравнимости по модулю  обладает следующими свойствами: обладает следующими свойствами:
- рефлексивности: для любого целого
 справедливо справедливо  - Симметричности если
 то то  - транзитивности: если
 и и  то то  Таким образом, отношение сравнимости по модулю  является отношением эквивалентности на множестве целых чисел[8]. является отношением эквивалентности на множестве целых чисел[8].
Кроме вышеперечисленных свойств, для сравнений справедливы следующие утверждения:
- любые два целых числа сравнимы по модулю 1.
- если числа
 и и  сравнимы по модулю сравнимы по модулю  , и , и 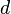 является делителем является делителем  , то , то  и и  сравнимы по модулю сравнимы по модулю 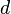 . . - если числа
 и и  сравнимы по нескольким модулям сравнимы по нескольким модулям  то они сравнимы по модулю, равному наименьшему общему кратному модулей: то они сравнимы по модулю, равному наименьшему общему кратному модулей:  . .
13) сравнение первой степени
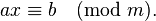
Решение такого сравнения начинается с вычисления 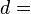 НОД НОД  . При этом возможны 2 случая: . При этом возможны 2 случая:
- Если
 не кратно не кратно 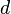 , то у сравнения нет решений. , то у сравнения нет решений. - Если
 кратно кратно 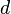 , то у сравнения существует единственное решение по модулю , то у сравнения существует единственное решение по модулю  , или, что то же самое, , или, что то же самое, 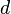 решений по модулю решений по модулю  . В этом случае в результате сокращения исходного сравнения на . В этом случае в результате сокращения исходного сравнения на 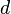 получается сравнение: получается сравнение: 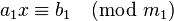
где  , ,  и и  являются целыми числами, причем являются целыми числами, причем  и и  взаимно просты. Поэтому число взаимно просты. Поэтому число  можно обратить по модулю можно обратить по модулю  , то есть найти такое число , то есть найти такое число  , что , что  (другими словами, (другими словами,  ). Теперь решение находится умножением полученного сравнения на ). Теперь решение находится умножением полученного сравнения на  : :
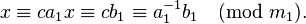
Практическое вычисление значения  можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение  в виде: в виде:
 [15]. [15].
Примеры
Пример 1. Для сравнения
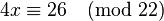
имеем  , поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2: , поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2:
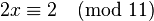
Поскольку 2 взаимно просто с модулем 11, то его можно обратить по модулю 11 и найти
 . .
Умножая сравнение на 6, получаем решение по модулю 11:
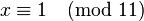 , ,
эквивалентное совокупности двух решений по модулю 22:
 и и  . .
20) кольцо классов вычетов
Множество всех чисел, сравнимых с  по модулю по модулю  , называется классом вычетов , называется классом вычетов  по модулю по модулю  , и обычно обозначается , и обычно обозначается  или или  . Таким образом, сравнение . Таким образом, сравнение  равносильно равенству классов вычетов равносильно равенству классов вычетов  [10]. [10].
Любое число класса называется вычетом по модулю  . Пусть для определенности . Пусть для определенности  ―остаток от деления любого из представителей выбранного класса на ―остаток от деления любого из представителей выбранного класса на  , тогда любое число , тогда любое число  из этого класса можно представить в виде из этого класса можно представить в виде  , где , где  —целое. Вычет равный остатку —целое. Вычет равный остатку  называется наименьшим неотрицательным вычетом, а вычет называется наименьшим неотрицательным вычетом, а вычет 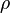 , самый малый по абсолютной величине, называется абсолютно наименьшим вычетом.При , самый малый по абсолютной величине, называется абсолютно наименьшим вычетом.При  , в противном случае , в противном случае  . Если . Если  -чётное и -чётное и  , то , то  [11]. [11].
Поскольку сравнимость по модулю  является отношением эквивалентности на множестве целых чисел является отношением эквивалентности на множестве целых чисел  , то классы вычетов по модулю , то классы вычетов по модулю  представляют собой классы эквивалентности; их количество равно представляют собой классы эквивалентности; их количество равно  . .
Множество всех классов вычетов по модулю  обозначается обозначается  или или 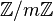 [12] или [12] или  [13]. [13].
Операции сложения и умножения на  индуцируют соответствующие операции на множестве индуцируют соответствующие операции на множестве  : :
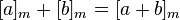

Относительно этих операций множество  является конечным кольцом, а для простого является конечным кольцом, а для простого  — конечным полем[6]. — конечным полем[6].
11)функции ейлера и ферма
Определение 1.10. Функция ϕ(n) натурального аргумента n > 2 равная количеству натуральных чисел взаимно простых с n называется функцией Эйлера.
Например ϕ(4) = 2, поскольку только 1 и 3 взаимно просты с 4 (а 2 и 4 — нет). Аналогично ϕ(6) = 2 и ϕ(9) = 6 (выпишите шесть нужных чисел!). Нетрудно видеть, что если p — проcтое число, то ϕ(p) = 1. Нам потребуется следующее простое утверждение.
Теорема 1.17 (Теорема Эйлера). Если a и n — взаимно простые натуральные числа, то aϕ(n) ≡ 1 (mod n).
Следствие 1.5 (Малая теорема Ферма). Если p простое число не делящее a, то ap−1 ≡ 1 (mod p).
Д о к а з а т е л ь с т в о. Возьмем n = p в теореме Эйлера и заметим, что ϕ(n) = ϕ(p) = p − 1. 
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


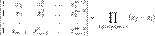
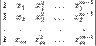
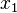 , из
, из  -го —
-го —  -й, уможенный на
-й, уможенный на  -го —
-го —  -й, уможенный на
-й, уможенный на 

 вынесем из
вынесем из  . Получим
. Получим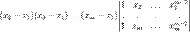
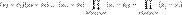
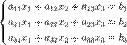
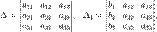
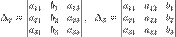
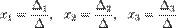
 показывает, что два выбранных целых числа при делении на
показывает, что два выбранных целых числа при делении на  и
и  записывается в виде формулы (сравнения):
записывается в виде формулы (сравнения):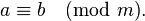
 , где
, где  — некоторое целое число[7].
— некоторое целое число[7].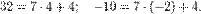

 то
то 
 и
и  то
то 
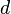 является делителем
является делителем  то они сравнимы по модулю, равному наименьшему общему кратному модулей:
то они сравнимы по модулю, равному наименьшему общему кратному модулей:  .
.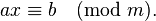
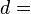 НОД
НОД  . При этом возможны 2 случая:
. При этом возможны 2 случая: , или, что то же самое,
, или, что то же самое, 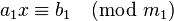
 ,
,  и
и  являются целыми числами, причем
являются целыми числами, причем  и
и  взаимно просты. Поэтому число
взаимно просты. Поэтому число  , то есть найти такое число
, то есть найти такое число  , что
, что  (другими словами,
(другими словами,  ). Теперь решение находится умножением полученного сравнения на
). Теперь решение находится умножением полученного сравнения на 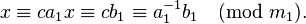
 [15].
[15].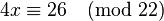
 , поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2:
, поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2: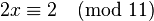
 .
.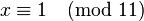 ,
, и
и  .
. или
или  . Таким образом, сравнение
. Таким образом, сравнение  [10].
[10]. ―остаток от деления любого из представителей выбранного класса на
―остаток от деления любого из представителей выбранного класса на  из этого класса можно представить в виде
из этого класса можно представить в виде  , где
, где  —целое. Вычет равный остатку
—целое. Вычет равный остатку 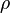 , самый малый по абсолютной величине, называется абсолютно наименьшим вычетом.При
, самый малый по абсолютной величине, называется абсолютно наименьшим вычетом.При  , в противном случае
, в противном случае  . Если
. Если  , то
, то  [11].
[11]. , то классы вычетов по модулю
, то классы вычетов по модулю  или
или 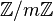 [12] или
[12] или  [13].
[13].