
|
|
МИНОРЫ И ТЕОРЕМА ЛАПЛАСА.Пусть В — некоторая матрица размером n x n. В = Опр. В квадратной матрице порядка n зафиксируем k ≤ n строк и столько же столбцов из элементов, которые стоят на пересечении фиксированных строк и столбцов, составляем матрицу, не нарушая взаимного расположения, определитель этой матрицы называется минором. Минор M’ расположенный в оставшихся строках называется дополнительным. Введем еще следующую сумму: SM = i1+ i2+ ...+ik + j1+ j2+ ...+jk. Сумма SM — это сумма номеров выделенных строк и выделенных столбцов. Тогда
Существует общий способ сведения вычисления определителей порядка n к вычислению определителей меньших порядков с применением понятия минора и алгебраического дополнения. Теорема Лапласа.Если в определителе порядка М зафиксировать к<n строк, тогда определитель матрицы равен сумме произведений всех миноров, содержащихся в выделенных строках, на их алгебраические дополнения, т.е. | B | = M1A1 + ... + MsAs. Следствие 1 (разложение определителя по строке).Определитель матрицы В равен сумме произведений элементов какой–нибудь строки на их алгебраические дополнения. < Следует из теоремы Лапласа при k = 1. > Следствие 2. Сумма произведений элементов строки определителя матрицы B на соответствующие дополнения к элементам другой строки равна нулю, т.е.. Пример: det ОПРЕДЕЛИТЕЛЬ ПРОИЗВЕДЕНИЯ МАТРИЦ. Теорема.Пусть А и В — две квадратные матрицы порядка n. Тогда определитель их произведения равен произведению определителей, т.е. | AB | = | A| | B |. < Пусть A = (aij) (n x n), B = (bij) (n x n). Рассмотрим определитель (d) (2n) порядка 2n A || (d) (2n) = || B
(d) (2n) = | A | | B | (-1)(^1+...+n+1+...+n) = | A | | B |. Если мы покажем, что определитель (d) (2n) равен определителю матрицы С=АВ, то теорема будет доказана. В (d) (2n) проделаем следующие преобразования: к 1 строке прибавим (n+1) строку, умноженную на а11; (n+2) строку, умноженную на а12 и т.д. (2n) строку, умноженную на (а) (1n) . В полученном определителе первые n элементов первой строки будут нулями, а n других элементов станут такими: a11* b11 + a12 * b21 + ... + (а) (1n) * (d) (1n) = c11; a11* b12 + a12 * b21 + ... + (а) (1n) * (d) (2n) = c12; ... a11* (d) (1n) + a12 * (d) (2n) + ... + (а) (1n) * (d) (nn) = (c) (1n). Аналогично получаем нули во 2, …, n строках определителя (d) (2n) , причем последние n элементов в каждой из этих строк станут соответствующими элементами матрицы С. В результате, определитель (d) (2n) преобразуется в равный ему определитель:
(d) (2n) = | C | (-1) )(^1+...+n+...+2n) = |AB|. > Следствие. Определитель произведения конечного числа квадратных матриц равен произведению их определителей.
ОБРАТНАЯ МАТРИЦА. Пусть A = (aij) (n x n) квадратная матрица над полем Р. Определение 1. Матрицу А будем называть вырожденной, если ее определитель равен 0. Матрицу А будем называть невырожденной в противном случае. Определение 2. Пусть АÎPn. Матрицу ВÎPn будем называть обратной к А, если АВ = ВА=Е. Теорема (критерий обратимости матрицы).Матрица А обратима <=> она невырожденная. < Пусть А имеет обратную матрицу. Тогда АА(^-1) = Е и, применяя теорему об умножении определителей, получаем | A | | A(^-1) | = | E | или | A | | A(^-1) | = 1. Следовательно, | A | ¹ 0. Пусть, обратно, | A | ¹ 0. Надо показать, что существует матрица В такая, что АВ = ВА = Е. В качестве В возьмем такую матрицу: В = АВ = Следует заметить, что в результате получится единичная матрица (достаточно воспользоваться следствиями 1 и 2 из теоремы Лапласа), т.е. АВ = Е. Аналогично показывается, что ВА = Е. > Пример. Для матрицы А найти обратную матрицу, или доказать, что ее нет. А = А11 = -3 А21 = 0 А31 = 6 А12 = 0 А22 = 0 А32=-3 А13 = 1 А23 = -1 А33 = -1 Итак, обратная матрица имеет вид: В =
КОЛЬЦО ПОЛИНОМОВ. Рассмотрим выражение:
Пусть А- коммутативное, ассоциативное кольцо с единицей, х — переменная, x^0, х^1, х^2…х^n-степени переменной, ai – коэффициенты полинома f(x), aixi - члены. Определение 1. Формальное выражение вида anхn+аn-1хn-1+…+а0 (1),где аn,…а0ÎР называют полиномом над полем Р от переменной х, аn,…а0 — коэффициенты полинома. Если аn¹0,то anхn называется старшим членом полинома, аn — старший коэффициент полинома. n=deg (полинома) — степень полинома. Множество полиномов над полем Р будем обозначать через Р[х], при этом полиномы будем обозначать так: f(x),g(x)… Степень полинома, у которого все коэффициенты равны нулю будем считать неопределенной. Иногда нулевому полиному приписывают степень, равную - ¥. Определение 2. Два полинома называют равными, если равны их коэффициенты, стоящие при одинаковых степенях. Сложение полиномов: f(x)=a0+a1 x+…+an x^n g(x)=b0+b1 x+…+bs x^s , s£n Под суммой полиномов f(x)+g(x) понимают полином f(x)+g(x)=c0+…+cn x^n , где cj=aj+bj. Очевидно, что сложение полиномаов коммутативно и ассоциативно, так как всё сводится к сложению элементов числового поля. Определение 3.Под произведением полиномов f(x)*g(x) понимают полином f(x)*g(x)= d0+…+dn+sxn+s, где
ДЕЛИМОСТЬ ПОЛИНОМОВ. Определение1.Пусть f(x), g(x)ÎР[х], где Р - поле. Будем говорить, что f(x) делит g(x) (обозначать f(x)ïg(x) ), если существует j(х)ÎР[х] такое, что g(x)=f(x)*j(х). Простейшие свойства: 1)Если g(x) делит fi(x), i=1..n, то g(x) делит 2)Если f(x) / g(x)и g(x) / m(x), тогда f(x) / m(x). 3)Если f(x) / g(x)и g(x) / f(x), то f(x)=ag(x),где aÎР. Докажем первое свойство: ◄g(x) / fi(x) следовательно $ многочлен ji(х), что fi(x) = g(x)ji(х), следовательно
Вынесем общий множитель g(x) за знак суммы. А это и означает, что g(x) делит сумму Второе свойство доказывается аналогично, как и для чисел. Докажем третье свойство: < f(x) / g(x)®g(x)=f(x)*m(x) (1) g(x) / f(x)®f(x)=g(x)*q(x) (2) Подставим (2) в (1): g(x)=g(x)*q(x)*m(x) Þ g(x)*(q(x)*m(x)-1)=0Þq(x)*m(x)=1. Из леммы следует, что степень q(x)= степени m(x)=0. Иначе говоря, что q(x) и m(x) — это элементы поля P. А это и доказывает свойство 3. > НОД ПОЛИНОМОВ. Определение 1.Полином d(x) называется общим делителем полиномов f (х) и g(x), если он является делителем каждого из них. Определение 2. НОДом двух ненулевых полиномов f(x) и g(x) называется их общий делитель, который делится на любой другой общий делитель этих полиномов. Лемма 1.Если f(x) = g (x) q (х) + r (х), то полиномы f (x), g(x) имеют те же общие делители, что и полиномы g(x), r(х). < Пусть d(x) — общий делитель f (х) и g(x). Так как r(х) = = f(x) — g(x)q(x), то d(x) делит г(х) и, следовательно, есть общий делитель g(x) и r(х). Аналогично всякий общий делитель g(x) и r (х) является общим делителем f (х) и g(x).> Теорема. НОД любых двух ненулевых полиномов f (х) и g(x) всегда существует. Он равен последнему отличному от нуля остатку в алгоритме Евклида, если g(x) не делит f(x), и совпадает с g(x) в противном случае. Теорема. Пусть d(x)=НОД (f(x),g(x)). Тогда существуют такие полиномы f (х) и y(х), что d(x)= f(x)*f (х)+ g(x) y(х)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
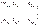 ,и kÎN, 1 ≤ k ≤ n.
,и kÎN, 1 ≤ k ≤ n. М1=Аm называется алгебраическим дополнением к минору М.
М1=Аm называется алгебраическим дополнением к минору М. = det
= det 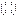 * det
* det  * (-1)(^1+2+1+2) = det
* (-1)(^1+2+1+2) = det 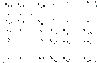

 ,где Аij — алгебраическое дополнение к элементу аij . Тогда
,где Аij — алгебраическое дополнение к элементу аij . Тогда

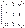 detA=-3 Þ обратная матрица существует. Теперь считаем алгебраические дополнения.
detA=-3 Þ обратная матрица существует. Теперь считаем алгебраические дополнения. =
= 
 =Sni=0aixi, aiÎA
=Sni=0aixi, aiÎA .
. .
.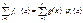
 . >
. >