
|
|
ДЕЛЕНИЕ С ОСТАТКОМ. АЛГОРИТМ ЕВКЛИДА. КРИТЕРИЙ ВЗАИМНОЙ ПРОСТОТЫ.Теорема о делении с остатком:Пусть f(x), g(x)ÎР[х], g(x)¹0. Тогда существует единственная пара полиномов q(x), r(x)ÎР[х], такая, что f(x)=g(x)*q(x)+r(x), где степень r(x)<степени g(x)либо r(x)=0. Алгоритм Евклида: Пусть f(x) и g(x) — два многочлена над полем Р. f(x) , g[x] ÎP[x]; g(x)¹ 0. Тогда можно разделить с остатком f(x) на g(x). f(x)=g(x)q(x)+r(x) , если r(x) ¹0, степень r(x)<степени g(x). Разделим g(x) на r(x) с остатком g(x)=r(x)q1(x)+r1(x), если r1(x) ¹0 степень r1 < степени r. Разделим r(x) на r1(x) и т.д. Так как степени остатков все время убывают, то на каком-то шаге остаток rk+1(x)=0. f(x)=g(x)q(x)+r(x) ; r(x) ¹0 g(x)=r(x) q1(x)+r1(x) ; r1(x) ¹0 ; cт. R1< ст. r (4) r(x)=r1(x)q2(x)+r2(x) ………………….. (r)(k-1) (x)=rk(x)(q) (k+1)(x)+ (r)(k+1) (x), (r)(k+1) (x)=0. Процесс последовательного получения равенств (4) называют алгоритмом Евклида для полиномов f(x) и g(x). Последний отличный от нуля остаток — rk. Определение.Полиномы f(x), g(x) называются взаимно простыми, если их НОД равен единице. Теорема 5 (критерий взаимной простоты). Полиномы f(x) и g(x) взаимно простоты <=> $ полиномы f (х) и y(х), такие, что f(x)f(х) + g(x)y(х)=1 < Þ Имеем f(x) и g(x) взаимно простые, то $ f(х) и y(х), такие, что f(x)f(х) + g(x)y(х)=1. Это следует из основного свойства НОД (Пусть d(x)=НОД (f(x),g(x)). Тогда существуют такие полиномы f (х) и y(х), что d(x)= f(x)f (х)+ g(x) y(х) ) Ü Пусть d(x)= НОД (f(x),g(x).Значит d(x) | 1 Þ d(x)=1 и значит полиномы взаимно простые.>
НЕПРИВОДИМЫЕ ПОЛИНОМЫ. Пусть f(x) ÎP[x], степень f(x) ≥ 1, очевидно, что a│f(x), aÎP, a ≠ 0. Определение.Если полином f(x) не имеет других делителей из Р[x], то он называется неприводимым полиномом над полем Р. Т.о. полином f(x)ÎP[х] степени n≥1 неприводим над полем Р тогда <=> из разложения f(х) = f(х)y(х), где f(х) ,y(х)ÎP[x], следует, что степень одного из полиномов f(х) ,y(х) равна нулю, а другого n. Многочлен f(x) называется приводимым над полем Р, если в кольце Р[х] существуют делители f(x), степени которых больше нуля, но меньше степени f(x). Другими словами, многочлен f(x) степени n≥ 1 приводим над полем Р <=> его можно представить в виде произведения двух многочленов из Р[х], степень каждого из которых меньше n. Простейшие свойства неприводимых многочленов: 1) Всякий полином первой степени неприводим (это следует из определения) f(x)=f1(x)f2(x), deg f(x)=1 Þ deg f1(x)=0 или 1, deg f2(x)=1 или 0; 2) Если f(x) неприводим над полем Р,то аf(x), где aÎP, a ≠ 0, тоже неприводим над полем Р; 3) Если f(x) неприводим над полем Ри g(x) ÎP[x] — некоторый полином над P , то ( f(x), g(x) )=1 либо f(x) │ g(x). < Рассмотрим НОД полиномов (f(x), g(x))=d(x).Значит d(x) │ g(x) и d(x) │ f(x) Þ d(x) равен 1, т.е. (f(x), g(x))=1 или 4) Если произведение полиномов f(x)g(x) делится на неприводимый полином h(x) , то хотя бы один из множителей f(x) или g(x) делится на h(x) < Пусть h(x) ∤ f(x) Þпо свойству 3 (h(x),f(x))=1 Þ Þ Теорема 1 (о разложении полинома на неприводимые множители). Всякий полином f(x)ÎP[x] степени ≥1 можно представить в виде произведения неприводимых над P полиномов. Разложение полинома на неприводимые множители определено однозначно с точностью до полинома нулевой степени и порядка следования сомножителей, то есть если имеется два разложения f(x) на неприводимые множители:f(x)= φ1(x)… φ S(x) = ψ1(x)… ψ k(x) , то s=k и при подходящей нумерации множителей : ψi =ai φi i = 1,…,s 0 ≠aiÎP. 21.поле комплексных чисел, комплексная полскость
Определим операцию сложения комплексных чисел по правилу
и определим операцию умножения:
Предложение 1. Множество Нулевым элементом в поле
33) Подстановки, умножение подстановок Определение. Всякое взаимно однозначное отображение множества А первых n натуральных чисел на себя называется подстановкой n-й степени, причем, очевидно, всякая подстановка А может быть записана при помощи двух перестановок, подписанных одна под другой
Через αi здесь обозначается то число, в которое при подстановке А переходит число i , i = 1, 2, …, n. Запишем одну под другой две перестановки из n символов, беря полученные две строки в скобки; например, n=5:
Умножение подстановок Определение. Произведением первой подстановки на вторую называют последовательное выполнение двух подстановок n-й степени, приводящее к некоторой вполне определенной третьей подстановке n-й степени. так, если даны подстановки четвертой степени
то
Невырожденные матрицы Невырожденная матрица (иначе неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае матрица называется вырожденной. Для квадратной матрицы M над полем невырожденность эквивалентна каждому из следующих условий:
38)Определитель Вандерморта Определителем Вандермонда называется определитель
Док-во База
Очевидно, её определитель равен 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , т.е. f(x) / g(x). >
, т.е. f(x) / g(x). > и
и  , ибо h(x) │ f(x)g(x) и h(x) │ g(x)h(x). >
, ибо h(x) │ f(x)g(x) и h(x) │ g(x)h(x). >
 Определение 2. Полем комплексных чисел называется множество всех упорядоченных пар действительных чисел . При этом каждая такая пара называется комплексным числом2).
Определение 2. Полем комплексных чисел называется множество всех упорядоченных пар действительных чисел . При этом каждая такая пара называется комплексным числом2).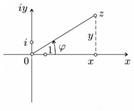 Таким образом, множество комплексных чисел можно интерпретировать как точки на плоскости
Таким образом, множество комплексных чисел можно интерпретировать как точки на плоскости  .
. для всех
для всех  ,
, для всех
для всех  .
. является полем
является полем является пара
является пара  , а единичным— пара
, а единичным— пара  . Противоположный элемент для
. Противоположный элемент для  , а обратным для ненулевого
, а обратным для ненулевого  .
. (1)
(1)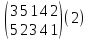
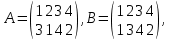
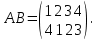
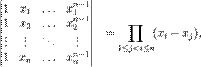
 . В данном случае матрица представляет собой
. В данном случае матрица представляет собой
 .
.