
|
|
Простейшие свойства колец.ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ГРУППЫ. Опр1.Пусть G не пустое множество элементов произвольной природы. G называется группой, если выполняются следующие условия: 1) На множестве G задана бао °. 2) бао ° ассоциативна. 3) Существует нейтральный элемент nÎG. 4) Для любого элемента из G симметричный ему элемент всегда существует и принадлежит такжеG. Пример. Множество Z – чисел с операцией +. Опр2.Группа называется абелевой, если она коммутативна относительно заданной бао °. Примеры групп: 1) Z,R,Q «+» (Z+) 2)R*=(R\{0},*) Q=(Q\{0},*) Z*=(Z\{0},*) Простейшие свойства групп В группе существует единственный нейтральный элемент В группе для каждого элемента существует единственный симметричный ему элемент Пусть G — группа с бао °, тогда уравнения вида : a°x=b и x°a=b (1) — разрешимы и имеют единственное решение. Доказательство. Рассмотрим уравнения (1) относительно x. Очевидно, что для а $! а'. Так как операция ° — ассоциативна, то очевидно x=b°a' — единственное решение. 34. ЧЕТНОСТЬ ПОДСТАНОВКИ* Определение 1. Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетная в противном случае. Предложение 1.Подстановка
из n чисел равно n!\2. Предложение 2. Подстановки f и f -1 имеют один характер четности. > Достаточно проверить, что если Пример:
ПОДГРУППА. КРИТЕРИЙ ПОДГРУППЫ. Опр.Пусть G — группа c бао ° и не пустое подмножество HÌG, тогда H называют подгруппой группы G, если H —подгруппа относительно бао° (т.е. ° - бао на Н. И Н с этой операцией группа). RÉQÉZ R*ÉQ* Теорема (критерий подгруппы).Пусть G — группа относительно операции°, ƹHÎG. H является подгруппой <=> "h1,h2ÎH выполняется условие h1°h2'ÎH (где h2' — симметричный элемент к h2). Док-во. =>:Пусть H — подгруппа (нужно доказать, что h1°h2'ÎH). Возьмем h1,h2ÎH, тогда h2'ÎH и h1°h'2ÎH (так как h'2 — симметричный элемент к h2). <=: (надо доказать, что H — подгруппа). Раз H¹Æ , то там есть хотя бы один элемент. Возьмем hÎH, n=h°h'ÎH, т.е. нейтральный элемент nÎH. В качестве h1 берем n, а в качестве h2 возьмём h тогда h'ÎH Þ " hÎH симметричный элемент к h также принадлежит H. Докажем, что композиция любых элементов из Н принадлежит Н. Возьмём h1 , а в качестве h2 возьмём h'2 Þ h1°(h2') ' ÎH, Þ h1°h2 ÎH. Пример.G=Sn, n>2, α — некоторый элемент из Х={1,…,n}. В качестве H возьмём не пустое множество H= Sαn ={fÎ Sn ,f(α)=α}, при действии отображения из Sαn α остаётся на месте. Проверяем по критерию. Возьмём любые h1,h2ÎH. Произведение h1.h2'ÎH, т.е H — подгруппа, которая называется стационарной подгруппой элемента α. КОЛЬЦО, ПОЛЕ. ПРИМЕРЫ. Опр.Пусть К непустое множество с двумя алгебраическими операциями: сложением и умножением. Кназывается кольцом, если выполняются следующие условия: 1)К—абелевагруппа(коммутативна относительно заданной бао °) относительно сложения; 2) умножение ассоциативно; 3)умножение дистрибутивно относительно сложения( Если умножение коммутативно, то К называют коммутативным кольцом. Если относительно умножения есть нейтральный элемент, то К называют кольцом с единицей. Примеры. 1)Множество Z целых чисел образует кольцо относительно обычных операций сложения и умножения. Это кольцо коммутативно, ассоциативно и обладает единицей. 2) Множества Q рациональных чисел и R действительных чисел являются полями относительно обычных операций сложения и умножения чисел. Простейшие свойства колец. 1. Так как К абелева группа относительно сложения, то на К переносятся простейшие свойства групп. 2. Умножение дистрибутивно относительно разности: a(b-c)=ab-ac. Доказательство. Т.к. ab-ac+ac=ab и a(b-c)+ac=a((b-c)+c)=a(b-c+c)=ab, то a(b-c)=ab-ac. 3. В кольце могут быть делители нуля, т.е. ab=0, но отсюда не следует,что a=0 Например, в кольце матриц размера 2´2, существуют элементы не равные нулю такие, что их произведение будет нуль: 4. a·0=0·а=0. Доказательство. Пусть 0=b-b. Тогда a(b-b)=ab-ab=0. Аналогично 0·а=0. 5. a(-b)=(-a)·b=-ab. Доказательство: a(-b)+ab=a((-b)+b)=a·0=0. 6. Если в кольце К существует единица и оно состоит более, чем из одного элемента, то единица не равна нулю, где 1─ нейтральный элемент при умножении; 0 ─ нейтральный элемент при сложении. 7. Пусть К кольцо с единицей, тогда множество обратимых элементов кольца образуют группу относительно умножения, которую называют мультипликативной группой кольца K и обозначают K*. Опр.Коммутативное кольцо с единицей, содержащее не менее двух элементов, в котором любой отличный от нуля элемент обратим, называется полем. Простейшие свойства поля 1. Т.к. поле — кольцо, то все свойства колец переносятся и на поле. 2. В поле нет делителей нуля ,т.е. если ab=0 ,то a=0 или b=0. Доказательство. Если a¹0 ,то $ a-1 . Рассмотрим a-1 (ab)=( a-1 a)b=0 , а если a¹0 ,то b=0, аналогично если b¹0 3. Уравнение вида a´x=b, a¹0, b – любое, в поле имеет единственное решение x= a-1b, или х=b/a. Решение этого уравнения называется частным. Примеры.1)PÌC, P — числовое поле. 2)P={0;1}; 3) P={0;1;2} . 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 является четной <=>
является четной <=>  — четная перестановка. Следовательно, количество четных подстановок
— четная перестановка. Следовательно, количество четных подстановок — произведение транспозиций, то
— произведение транспозиций, то  <
<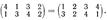
 ).
). b=0.
b=0.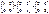 ,где
,где  — играет роль нулевого элемента.
— играет роль нулевого элемента.