
|
|
СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Для того чтобы система тел начала колебательное движение, ее нужно вывести из положения равновесия, т. е. совершить некоторую работу. При этом система тел приобретает энергию, равную по величине выполненной работе.
Если теперь мы отпустим тело, то оно начнет двигаться к положению равновесия О так, что его смещение будет гармонической функцией времени (VI. 1).
Для пружинного маятника на рис. 106 мы вы- бирали такие начальные условия, что амплитуда тела равна А, а начальная фаза равна j0 = - p/2:
Действительно, в начальный момент времени t = 0 смещение равно
После начала движения величина смещения груза уменьшается, значит, уменьшаются сила, действую- щая на груз, и потенциальная энергия. В точке О сила упругости равна нулю и потенциальная энергия маятника также равна нулю: Еп(0) = 0. Скорость тела, наоборот, увеличивается, а значит, увеличивается и кинетическая энергия. Величину скорости в точке О можно определить по формуле (VI.2). Сначала найдём фазу колебания при первом прохождении тела через точку положения равновесия. Время от начала движения до точки О равно одной четверти периода колебаний t1 = Следовательно, фаза колебания маятника в точке О равна
Теперь по формуле (VI.2) находим, что скорость груза при прохождении точки положения равновесия имеет максимальное значение: υ = w × А×cos 0 = w×А Значит, кинетическая энергия в точке О также имеет максимальное значение
Полная энергия пружинного маятника в точке О равна кинетической энергии груза:
При дальнейшем движении груза его кине- тическая энергия начинает уменьшаться, а потенци- альная энергия — увеличиваться. В точке х = А кинетическая энергия становится равной нулю, а по-тенциальная энергия снова принимает максимальное значение. Затем цикл повторяется. Рассматривая модель пружинного маятника, мы считаем, что груз движется без трения, т.е. работа против сил трения равна нулю. Тогда по закону сохра-
т. е. закон сохранения полной механической энергии выполняется. Таким образом, мы видим, что энергия гармонических колебаний пружинного маятника остаётся постоянной, но периодически превращается из потенциальной в кинетическую и обратно. В общем случае полная энергия свободных гармонических колебаний определяется по формуле
Полная механическая энергия свободных гармонических колебаний прямо пропорциональна квадрату частоты и квадрату амплитуды колебаний.
??? ОТВЕТЬТЕ НА ВОПРОСЫ: 1. Зависит ли полная энергия пружинного маятника и математического маятника от массы тела? 2. Фаза колебаний равна 3p/4. Величина какого вида энергии — кинетической или потенциальной — больше при этом значении фазы?
4. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
При изучении математического и пружинного маятника мы считали, что сил трения нет. Энергия колебательного движения при этом остаётся постоянной. Амплитуда колебаний также остаётся по- стоянной. Н е з а т у х а ю щ и м и к о л е б а н и я м и называются такие колебания, амплитуда которых не изменяется со временем А = const.
Все реальные свободные колебания являются затухающими. Незатухающими для реальной системы тел могут быть только вынужденные колебания, которые происходят под действием периодически изменяющейся со временем внешней силы. Рассмотрим, как изменяются характеристики движения колебательной системы тел при вынужденных колебаниях. Опыт и теория показывает, что амплитуда и частота вынужденных колебаний зависят от частоты изменения внешней силы.
При изменении частоты f изменения внешней силы
5. ВОЛНЫ
Волновое движение, или упругие волны, — это процесс распространения колебаний в упругой среде. Различают два вида волн: поперечные волны и продольные волны.
Например, механическая поперечная волна распространяется вдоль длинного упругого шнура, если один его конец резко перемещать в перпендикулярном шнуру направлении (рис. 109).
В том случае, когда смещение частиц среды изменяется со временем по закону синуса, в среде распространяется синусоидальная, или гармоническая волна. График зависимости смещения частиц среды в синусоидальной волне от координаты Х вдоль направления распространения показан на рис. 110.
Д л и н а в о л н ы — это расстояние, на которое распространяется колебание за один период. Зная длину волны и период колебаний частиц среды, мы можем найти вторую характеристику волнового движения — с к о р о с т ь р а с п р о с т- р а н е н и я к о л е б а н и й (скорость волны)
На опыте установлено, что скорость волны зависит от вида, состояния и упругих свойств среды. Механические поперечные волны могут распространяться только в твёрдых средах. П р о д о л ь н ы м и называются такие волны, в которых частицы среды колеблются вдоль направления распространения волны.
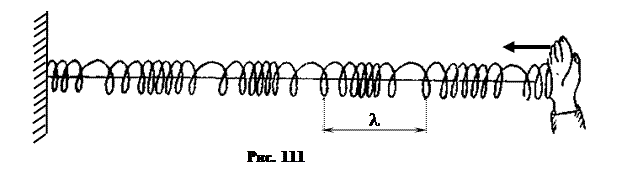
Продольные волны могут распространяться в любой среде: твёрдой, жидкой и газообразной. Например, продольная волна распространяется вдоль спиральной пружины, если пружину ударить по одному концу (рис. 111). Важнейший пример продольных волн — звуковые волны. З в у к о в ы м и в о л н а м и называются продольные упругие волны, которые распространяются в упругой среде (твёрдых телах, жидкостях и газах). Человек может слышать звуковые колебания (звук); частота этих колебаний лежит в интервале от 16 до 20 000 Гц. Колебания с частотой меньше 16 Гц (инфразвук) и больше 20 000 Гц (ультразвук) человек слышать не может. Наиболее часто мы встречаемся со звуковыми колебаниями в воздухе, где процесс распространения звуковых волн связан с периодическим увеличением и уменьшением давления воздуха (рис. 112). Скорость распространения звуковых волн в воздухе (скорость звука) при температуре 00С и нормальном атмосферном давлении (760 мм рт. ст.) равна »332 м/с. При повышении температуры и давления воздуха скорость звука возрастает.
Основными характеристиками звуковых колебаний являются громкость, высота и тембр. Г р о м к о с т ь з в у к а ¾ это его энергетическая характеристика, которая оценивается по субъективному слуховому восприятию звука. Объективной энергетической характеристикой звука является его интенсивность. И н т е н с и в н о с т ь з в у к а ¾ это физическая величина, равная энергии, переносимой звуковой волной за единицу времени через единицу площади поверхности, перпендикулярной направлению распространения волны.
В ы с о т а з в у к а характеризуется частотой колебаний (или длиной волны). Чем больше частота (чем меньше длина волны), тем выше звук. Прибор, с помощью которого можно получить звуковые колебания заданной частоты, называется камертоном. На рис. 112 источником звуковых волн является камертон. Т е м б р — это качественная характеристика звука. Реальные звуковые колебания всегда складываются из нескольких гармонических колебаний частиц среды. При этом каждое отдельное колебание имеет свою частоту и амплитуду. Тембр звука определяется набором частот этих гармонических колебаний в данном звуке и их амплитудами.
??? ОТВЕТЬТЕ НА ВОПРОСЫ: 1. Какие главные характеристики волнового движения вы знаете? 2. В чём различие поперечных и продольных волн? 3. От чего зависит скорость звука в воздухе?
СЛОВАРИ
ВВЕДЕНИЕ.. 3 1. ПРЕДМЕТ ФИЗИКА.. 3 1.1. Что изучает физика?. 3 1.2. Физическая величина. 3 1.3. Методы определения физических величин.. 4 1.4. Единицы измерения физических величин.. 5 1.5. Система единиц.. 7 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ... 9 2.1. Скалярные величины.. 9 2.2. Векторные величины.. 9 3. ДЕЙСТВИЯ С ВЕКТОРАМИ.. 10 3.1. Сравнение векторов. 10 3.2. Сложение векторов. 10 3.3. Вычитание векторов. 12 3.4. Умножение вектора на скаляр. 12 3.5. Разложение вектора на составляющие. 13 3.6. Проекция вектора на оси координат. 14 МЕХАНИКА.. 18 Ⅰ. КИНЕМАТИКА.. 18 1. ОСНОВНЫЕ ПОНЯТИЯ И ХАРАКТЕРИСТИКИ КИНЕМАТИКИ.. 18 1.1. Материальная точка. 18 1.2. Траектория. 19 1.3. Путь. 19 1.4. Время. 19 1.5. Тело отсчёта. 20 1.6. Система координат. 20 1.7. Система отсчёта. 21 1.8. Радиус-вектор 1.9. Перемещение 1.10. Скорость 1.11. Изменение скорости 1.12. Ускорение 2. ВИДЫ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ.. 27 2.1. Прямолинейное движение. 27 2.2. Криволинейное движение. 27 2.3. Равномерное движение. 27 2.4. Неравномерное движение. 28 3. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ.. 29 3.1. Формулы прямолинейного равномерного движения. 29 3.2. Графики прямолинейного равномерного движения. 30 4. ПРЯМОЛИНЕЙНОЕ НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ.. 31 4.1. Прямолинейное равнопеременное движение. 32 4.2. Основные формулы прямолинейного равнопеременного движения. 33 4.3. Графики равнопеременного движения. 34 4.4. Свободное падение. 35 4.5. Движение тела, брошенного вертикально вверх. 36 5. КИНЕМАТИКА РАВНОМЕРНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ.. 39 Ⅱ. ДИНАМИКА.. 44 1. НЕКОТОРЫЕ ДИНАМИЧЕСКИЕ ПОНЯТИЯ И ХАРАКТЕРИСТИКИ.. 44 2. ЗАКОНЫ НЬЮТОНА.. 46 2.1. Первый закон Ньютона (закон инерции) 46 2.2. Второй закон Ньютона. 46
 2.3. Третий закон Ньютона. 48 2.3. Третий закон Ньютона. 48
3. ВИДЫ СИЛ В МЕХАНИКЕ.. 49 3.1. Силы упругости.. 49 3.2. Силы трения. 52 3.3. Силы гравитации.. 54 3.4. Вес тела. Невесомость. 56 4. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА СИСТЕМЫ ТЕЛ.. 58 4.1. Система тел. 58 4.2. Закон сохранения импульса. 59 5. ДИНАМИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ.. 62 III. МЕХАНИЧЕСКАЯ РАБОТА И ЭНЕРГИЯ.. 65 1. МЕХАНИЧЕСКАЯ РАБОТА.. 65 1.1. Работа постоянной силы.. 65 1.2. Работа переменной силы.. 68 2. КОНСЕРВАТИВНЫЕ И НЕКОНСЕРВАТИВНЫЕ СИЛЫ. РАБОТА КОНСЕРВАТИВНЫХ СИЛ.. 70 2.1. Работа силы упругости.. 70 2.2. Работа силы тяжести.. 71 2.3. Работа силы трения. 72 3. МОЩНОСТЬ. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ.. 73 3.1. Мощность. 73 3.2. Коэффициент полезного действия. 74 4. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ.. 75 4.1. Потенциальная энергия. 76 4.2. Кинетическая энергия. 79 4.3. Законы сохранения и изменения механической энергии.. 80 IV. СТАТИКА.. 85 1. СТАТИКА ТЕЛА, НЕ ИМЕЮЩЕГО НЕПОДВИЖНОЙ ОСИ ВРАЩЕНИЯ.. 85 2. СТАТИКА ТЕЛА, ИМЕЮЩЕГО НЕПОДВИЖНУЮ ОСЬ ВРАЩЕНИЯ.. 87 3. ОБЩЕЕ УСЛОВИЕ РАВНОВЕСИЯ ТЕЛА.. 90 4. РАВНОВЕСИЕ ТЕЛА ПОД ДЕЙСТВИЕМ ПАРАЛЛЕЛЬНЫХ СИЛ.. 90 5. РАВНОВЕСИЕ ТЕЛ В ОДНОРОДНОМ ПОЛЕ СИЛ ТЯЖЕСТИ.. 92 6. ВИДЫ РАВНОВЕСИЯ.. 95 Ⅴ. ГИДРОСТАТИКА.. 99 1. СИЛА ДАВЛЕНИЯ В ЖИДКОСТИ. ДАВЛЕНИЕ.. 99 2. ЗАКОН ПАСКАЛЯ.. 100 3. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ.. 102 4. СООБЩАЮЩИЕСЯ СОСУДЫ... 103 5. ЗАКОН АРХИМЕДА.. 104 VI. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ.. 108 1. ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ.. 109 2. ДИНАМИКА СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ.. 113 3. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ.. 118 4. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ.. 121 5. ВОЛНЫ... 122 СЛОВАРИ.. 127
 

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рассмотрим на примере пружинного маятника, как изменяется энергия системы тел при свободных гармонических колебаниях (рис. 106). Пусть груз массой т находится в покое в положении равновесия (точка О). Переместим тело в точку х = -А. При этом мы сжимаем пружину и совершаем работу против силы упругости
Рассмотрим на примере пружинного маятника, как изменяется энергия системы тел при свободных гармонических колебаниях (рис. 106). Пусть груз массой т находится в покое в положении равновесия (точка О). Переместим тело в точку х = -А. При этом мы сжимаем пружину и совершаем работу против силы упругости 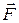 , а пружинный маятник приобретает энергию, которая равна по величине выполненной работе. Механическая энергия сжатой пружины — это потенциальная энергия, величина которой опреде-
, а пружинный маятник приобретает энергию, которая равна по величине выполненной работе. Механическая энергия сжатой пружины — это потенциальная энергия, величина которой опреде- , где k — коэффициент упругости пружины. Так как тело в точке х = -А не движется, его кинетическая энергия здесь равна нулю Ек (-А) = 0. Следовательно, полная энергия в точке х = - А равна потенциальной энергии
, где k — коэффициент упругости пружины. Так как тело в точке х = -А не движется, его кинетическая энергия здесь равна нулю Ек (-А) = 0. Следовательно, полная энергия в точке х = - А равна потенциальной энергии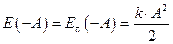 . (VI.13, а)
. (VI.13, а)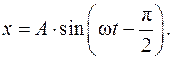
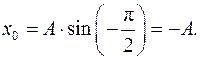

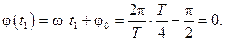
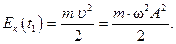
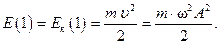 (VI.13, б)
(VI.13, б)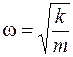 ,
,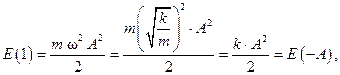
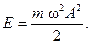 (VI.14)
(VI.14)
 В реальных колебательных системах силы трения всегда присутствуют. В таких системах часть полной энергии расходуется на совершение работы против сил трения, поэтому полная энергия свободных колебаний всё время уменьшается. В результате амплитуда колебаний также постоянно уменьшается и через не- которое время колебания прекращаются.
В реальных колебательных системах силы трения всегда присутствуют. В таких системах часть полной энергии расходуется на совершение работы против сил трения, поэтому полная энергия свободных колебаний всё время уменьшается. В результате амплитуда колебаний также постоянно уменьшается и через не- которое время колебания прекращаются. Пример зависимости амплитуды затухающих колебаний от времени показан на рис. 107.
Пример зависимости амплитуды затухающих колебаний от времени показан на рис. 107. Частота вынужденных колебаний равна частоте изменения внешней силы (период вынужденных колебаний равен периоду изменения внешней силы).
Частота вынужденных колебаний равна частоте изменения внешней силы (период вынужденных колебаний равен периоду изменения внешней силы). П о п е р е ч н ы м и называются такие волны, в которых частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны.
П о п е р е ч н ы м и называются такие волны, в которых частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны.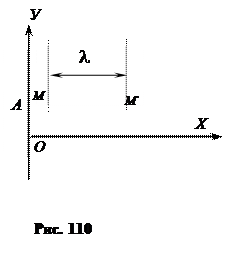
 Рассмотрим на графике две частицы М и М', которые колеблются вдоль оси ОУ. Расстояние между этими частицами обозначим греческой буквой l (ламбда). Из рисунка видно, что частица М совершила на одно полное колебание больше, чем частица М'. Поэтому можно сделать вывод, что фаза колебания частицы М на 2p больше, чем фаза колебания частицы М'. Время, за которое колебание распространяется от частицы М к частице М', равно периоду колебаний частиц Т. Таким образом, за время Т колебание распространяется на расстояние l, которое является характеристикой волнового движения и называется длиной волны.
Рассмотрим на графике две частицы М и М', которые колеблются вдоль оси ОУ. Расстояние между этими частицами обозначим греческой буквой l (ламбда). Из рисунка видно, что частица М совершила на одно полное колебание больше, чем частица М'. Поэтому можно сделать вывод, что фаза колебания частицы М на 2p больше, чем фаза колебания частицы М'. Время, за которое колебание распространяется от частицы М к частице М', равно периоду колебаний частиц Т. Таким образом, за время Т колебание распространяется на расстояние l, которое является характеристикой волнового движения и называется длиной волны.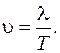

 .... 22
.... 22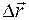 ......... 22
......... 22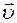 ..... 23
..... 23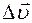 .......... 24
.......... 24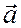 ...... 25
...... 25