
|
|
РАВНОВЕСИЕ ТЕЛ В ОДНОРОДНОМ ПОЛЕ СИЛ ТЯЖЕСТИ
Вблизи поверхности Земли существует одно- родное поле сил тяжести. Это значит, что в любой точке пространства на тело массы т действует одинаковая сила Рассмотрим равновесие системы абсолютно твёрдых тел в однородном поле сил тяжести. Пусть на невесомом и недеформируемом горизонтальном стерж- не на расстояниях хi от точки О закреплены n грузов массами mi (рис. 85), i = 1, 2, ..., n. На отдельные части системы тел (на каждое тело) действуют силы тяжести
Равнодействующую всех сил тяжести Силы тяжести, действующие на отдельные части тела или системы тел, — это частный случай парал- лельных сил. Решая задачу о сложении параллельных сил, из формулы (IV.4а) находим модуль равнодействующей силы, равный модулю силы реакции опоры
Координату х точки, в которой приложена равнодействующая
где моменты сил вычислены относительно точки О; момент силы реакции опоры:
х Точка приложения равнодействующей всех сил тяжести, действующих на отдельные части тела (или системы тел), называется ц е н т р о м т я ж е с т и т е л а (или системы тел). В рассмотренном нами примере формула (IV.6) определяет координату центра тяжести системы тел, если известны масса и координаты точек приложения сил тяжести каждой части этой системы тел. Центр тяжести однородных тел правильной формы находится в их геометрическом центре (рис. 86): — центр тяжести однородного стержня лежит на его середине; — центр тяжести однородного куба или параллелепипеда лежит на пересечении его больших диагоналей; — центр тяжести однородного цилиндра находится на середине оси его симметрии; — центр тяжести однородного диска, Если плоское тело имеет неправильную форму, то найти положение его центра тяжести можно с помощью опыта. Подвесим тело на нити сначала в некоторой точке А (рис. 87, а). При этом линия действия силы натяжения нити Проведём на плоской поверхности тела линию ВС. Тогда центр тяжести С определится как точка пересечения линий ВС и АС. Можно проверить, что все линии, проведённые из точки подвеса тела вертикально вниз, пересекаются в центре тяжести тела, т.е. в точке С.
ВИДЫ РАВНОВЕСИЯ
В статике абсолютно твёрдого тела различают три вида равновесия.
Если отклонить шарик от положения равновесия, то векторная сумма сил тяжести и реакции опоры уже не равна нулю: возникает сила Это пример устойчивого равновесия. У с т о й ч и в ы м называется такой вид равновесия, при выходе из которого возникают силы или моменты сил, которые стремятся вернуть тело в положение равновесия. Потенциальная энергия шарика в любой точке вогнутой поверхности больше, чем потенциальная энергия в положении равновесия (в точке О). Например, в точке А (рис. 88) потенциальная энергия больше, чем потенциальная энергия в точке О на величину Еп(А) - Еп(0) = mgh. В положении устойчивого равновесия потенци- альная энергия тела имеет минимальное значение по сравнению с соседними положениями.
Под действием силы Н е у с т о й ч и в ы м называется такой вид равновесия, при выходе из которого возникают силы или моменты сил, которые стремятся увести тело ещё дальше от положения равновесия. Потенциальная энергия шарика на выпуклой поверхности имеет наибольшее значение (максимум) в точке О. В любой другой точке потенциальная энергия шарика меньше. Например, в точке А (рис. 89) потенциальная энергия меньше, чем в точке О, на величину Еп(0) - Еп(А) = mgh.
3. На горизонтальной поверхности силы, действующие на шарик, уравновешены в любой точке: Это пример безразличного равновесия. Б е з р а з л и ч н ы м называется такой вид равновесия, при выходе из которого тело остаётся в новом положении в равновесии. Потенциальная энергия шарика во всех точках горизонтальной поверхности (рис. 90) одинакова. В положениях безразличного равновесия потен- циальная энергия одинакова. Иногда на практике приходится определять вид равновесия тел различной формы в поле сил тяжести. Для этого нужно запомнить следующие правила: 1. Тело может находиться в положении устой- чивого равновесия, если точка приложения силы реакции опоры находится выше центра тяжести тела. При этом эти точки лежат на одной вертикали (рис. 91).
2. Когда точка приложения силы реакции опоры находится ниже центра тяжести, возможны два случая: — если опора точечная (площадь поверхности опоры мала), то равновесие неустойчивое (рис. 92). При небольшом отклонении от положения равновесия момент сил
??? ОТВЕТЬТЕ НА ВОПРОСЫ: 1. Как изменяется положение центра тяжести тела, если тело вывести из положения: а) устойчивого равновесия? б) неустойчивого равновесия? 2. Как изменяется потенциальная энергия тела, если изменить его положение при безразличном равновесии?
Ⅴ. ГИДРОСТАТИКА

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , всегда направленная вертикаль- но вниз.
, всегда направленная вертикаль- но вниз. , направленные вертикально вниз.
, направленные вертикально вниз. Для того чтобы система тел находилась в равновесии, в некоторой точке с координатой х должна быть опора.
Для того чтобы система тел находилась в равновесии, в некоторой точке с координатой х должна быть опора. уравновешивает сила реакции опоры
уравновешивает сила реакции опоры  , которая направлена вертикально вверх. Мы видим, что линии действия всех сил параллельны, т.е. на систему тел действуют параллельные силы.
, которая направлена вертикально вверх. Мы видим, что линии действия всех сил параллельны, т.е. на систему тел действуют параллельные силы. : (IV.5)
: (IV.5)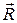 всех сил тяжести (и сила реакции опоры
всех сил тяжести (и сила реакции опоры 
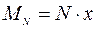 , моменты сил тяжести:
, моменты сил тяжести:  .
. После подстановки в последнее уравнение значений моментов сил и величины силы реакции опоры (IV.5) получаем значение координаты точки приложения равнодействующей сил тяжести
После подстановки в последнее уравнение значений моментов сил и величины силы реакции опоры (IV.5) получаем значение координаты точки приложения равнодействующей сил тяжести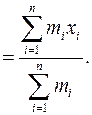 (IV.6)
(IV.6) , уравновешивающей силу тяжести
, уравновешивающей силу тяжести  1. Рассмотрим шарик, который находится на вогнутой поверхности. В положении, показанном на рис. 88, шарик находится в равновесии: сила реакции опоры
1. Рассмотрим шарик, который находится на вогнутой поверхности. В положении, показанном на рис. 88, шарик находится в равновесии: сила реакции опоры  , которая стремится вернуть шарик в первоначальное положение равновесия (в точку О).
, которая стремится вернуть шарик в первоначальное положение равновесия (в точку О). 2. Шарик на выпуклой поверхности находится в положении равновесия в верхней точке (рис. 89), где сила тяжести
2. Шарик на выпуклой поверхности находится в положении равновесия в верхней точке (рис. 89), где сила тяжести 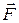 шарик будет удаляться от точки О. Это пример неустойчивого равновесия.
шарик будет удаляться от точки О. Это пример неустойчивого равновесия. В положении неустойчивого равновесия потен-циальная энергия тела имеет максимальное значение по сравнению с соседними положениями.
В положении неустойчивого равновесия потен-циальная энергия тела имеет максимальное значение по сравнению с соседними положениями.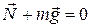 (рис. 90). Если, например, сместить шарик из точки О в точку А, то равнодействующая сил
(рис. 90). Если, например, сместить шарик из точки О в точку А, то равнодействующая сил На рис. 91, б роль силы реакции опоры играет сила натяжения нити
На рис. 91, б роль силы реакции опоры играет сила натяжения нити  стремится увеличить отклонение от начального положения;
стремится увеличить отклонение от начального положения; — если опора неточечная (площадь поверх- ности опоры велика), то положение равновесия устой- чивое в том случае, когда линия действия силы тяжести АА' пересекает поверхность опоры тела
— если опора неточечная (площадь поверх- ности опоры велика), то положение равновесия устой- чивое в том случае, когда линия действия силы тяжести АА' пересекает поверхность опоры тела 
 Координаты центра тяжести системы тел:
Координаты центра тяжести системы тел:
 ;
;  ;
;  Момент пары сил
M = F× ℓ
Момент пары сил
M = F× ℓ