
|
|
ВИДЫ МЕХАНИЧЕСКОГО ДВИЖЕНИЯВВЕДЕНИЕ
1. ПРЕДМЕТ ФИЗИКА
1.1. Что изучает физика? Физика — это наука о природе. Физика изучает физические тела, физические процессы и физические явления. Например: — стол, дом, Солнце, вода, воздух — это физические тела; —камень падает — это физический процесс; —автобус движется — это физический процесс; —идёт дождь — это физическое явление.
1.2. Физическая величина
Пример (рис. 1). Это тело. Тело имеет массу, длину, объем. Длина, масса, объем — это характеристики тела. Длина, масса, объем — это физические величины.
Скорость автобуса равна 60 км/ч (шестидесяти километрам в час). Скорость — это характеристика движения (характеристика физического процесса). Скорость — это физическая величина. Физические величины мы обозначаем буквами латинского алфавита и греческого алфавита, например: — массу мы обозначаем буквой m (читаем «эм»), — длину мы обозначаем буквой ℓ (читаем «эль»), — время мы обозначаем буквой t (читаем «тэ»), — плотность мы обозначаем буквой ρ (читаем «ро»).
1.3. Методы определения физических величин
Пример (рис. 3). 1. Длину тела ℓ мы измеряем линейкой (рис. 3, а). Линейка — это прибор для измерения длины. 2. Массу тела m мы измеряем на весах (рис. 3, б). Весы — это прибор для измерения массы. 3.
Пример (рис. 4). Тело имеет форму параллелепипеда. Объем параллелепипеда мы определяем по формуле.
Если мы знаем массу тела m и объем V, то мы можем найти плотность вещества ρ (читаем «ро») по формуле
Мы можем найти по формулам и другие физические величины, например скорость, силу, работу. С д е л а е м в ы в о д ы: 1) физическую величину мы можем измерить физическим прибором; 2) физическую величину мы можем найти по формуле.
1.4. Единицы измерения физических величин
Е д и н и ц ы д л и н ы
1 км = 1000 м (один километр равен тысяче метров), 1 м = 100 см (один метр равен ста сантиметрам), 1см = 10 мм (один сантиметр равен десяти миллиметрам). Единица измерения обозначается символом физической величины в квадратных скобках: [ℓ] = 1 м, [ℓ] = 1 см, [ℓ] = 1 км.
Е д и н и ц ы м а с с ы
1 кг (один килограмм), 1 г (один грамм), 1 т (одна тонна) — это единицы массы. [m] = 1 кг, [m] = 1 г, [m] == 1 т. 1 т = 1000 кг (в одной тонне — тысяча килограммов), 1 кг = 1000 г (в одном килограмме — тысяча граммов), 1 г =1000 мг (в одном грамме — тысяча миллиграммов).
Е д и н и ц ы в р е м е н и
1 ч (один час), 1 мин (одна минута), 1 с (одна секунда) — это единицы времени. [t] = 1 ч, [t] = 1 мин., [t] = 1 с. 1 ч = 60 мин (один час равен шестидесяти минутам), 1 мин. = 60 с (одна минута равна шестидесяти секундам), 1 ч = 3600 с (один час равен трём тысячам шестистам секундам).
Рассмотрим некоторые производные единицы измерения.
Е д и н и ц ы о б ъ ё м а
Формула объема параллелепипеда V = ℓ·b·d. В этой формуле ℓ, b и d измеряются в единицах длины, например в метрах или в сантиметрах. Тогда единицы объема: [V] = [ℓ] 3. [V] = l м3 (один кубический метр) или [V] =1 см3 (один кубический сантиметр). Е д и н и ц ы п л о т н о с т и Формула плотности вещества Если масса измеряется в килограммах, а объём — в кубических метрах, то единица плотности
Единицы измерения объема, плотности, скорости, силы, работы и других физических величин — это производные единицы.
1.5. Система единиц
Система единиц состоит из основных и производных единиц.
единица длины [ℓ] = 1 м — один метр, единица массы [m] = 1 кг — один килограмм, единица времени [t] = 1 с — одна секунда.
Единицы измерения других физических величин — производные единицы: единица скорости [υ] = 1 м/с — один метр в секунду, единица ускорения [а] = 1 м/с2 — один метр на секунду в квадрате, единица силы [F] — 1 кг·м/с2 = 1 Н — один ньютон, единица работы [А] = 1 Н·м = 1 Дж — один джоуль, единица плотности [ρ] = 1 кг/м3 — один килограмм на кубический метр.
единица массы [m] = 1 г (один грамм), единица времени [t] = 1 с (одна секунда).
Некоторые производные единицы в СГС: единица скорости [υ] = 1 см/с, единица ускорения [а] = 1 см/с2, единица силы [F] = 1 г×см/с2 = 1 дин — одна дина, единица работы [А] = 1 дин·см = 1 г×см 2 /с2 = 1 эрг. Мы можем переводить единицы измерения из одной системы единиц в другую. Например, единица плотности в СИ [ρ] = 1 кг/м3. Найдем значение этой единицы в системе СГС: 1 кг/м3 = 1 кг/1м3 = 103 г/106 см3= 10-3 г/см3.
??? ОТВЕТЬТЕ НА ВОПРОСЫ: 1. Что изучает физика? 2. акие физические тела вы знаете? 3. Какие физические величины вы знаете? 4. Каким прибором мы измеряем длину? 5. Какую физическую величину измеряют секундомером? 6. Сколько сантиметров в одном километре? 7. Сколько секунд в одном часе?
2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ
2.1. Скалярные величины С к а л я р н а я в е л и ч и н а — это физическая величина, которая имеет численное значение и единицу измерения. Скалярная величина может быть положительной или отрицательной. Примеры скалярных величин: температура, масса, объём, время, плотность. Математические действия со скалярными величинами — это алгебраические действия с числами.
В е к т о р н а я в е л и ч и н а — это физическая величина, которая имеет: 1) численное значение, которое всегда положительно (модуль вектора); 2) направление; 3) единицу измерения. Примеры векторных физических величин: скорость, ускорение, сила. Векторная величина обозначается буквой и стрелкой над этой буквой. Например: — вектор скорости обозначается символом — вектор ускорения обозначается символом
Модуль вектора обозначается так:
½
½
|
На рисунке (графически) вектор изображается направленным отрезком прямой линии (рис. 5). Модуль вектора равен длине отрезка в зáданном масштабе (рис. 6).
3. ДЕЙСТВИЯ С ВЕКТОРАМИ
3.1. Сравнение векторов Рассмотрим два вектора
Равные векторы. ( — равные модули, — одинаковые направления. Равнопротивоположные векторы. ( — равные модули, — противоположные направления. 3.2. Сложение векторов Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника. Пусть заданы два вектора Найдём сумму этих векторов Векторы
1. Нарисуем вектор 2. Нарисуем вектор 3. Через конец вектора 4. Через конец вектора прямую линию, параллельную вектору 5. Проведем диагональ параллелограмма из общей точки начала вектора 6. Модуль результирующего вектора начало вектора Правило треугольника для сложения 1. Нарисуем составляющие векторы 2. Результирующий вектор Модуль результирующего вектора находим по формуле
Пусть заданы два вектора
вектор вектор вектор
Найти разность вектора
Правило параллелограмма. Стороны параллелограмма — вектор Правило треугольника.
Вариант 2. Вектор разности
Пусть заданы вектор В результате умножения вектора на скаляр мы получаем новый вектор
Направление вектора Направление вектора Модуль вектора
3.5. Разложение вектора на составляющие
Разложить вектор — направления которых совпадают c зáданными направлениями; — сумма которых равна вектору
Геометрически разложить вектор на составляющие векторы — это значит построить параллелограмм по зáданной диагонали и зáданным направлениям сторон. Найдём составляющие вектора 1. Через начало и конец вектора 2. Через начало и конец вектора Мы построили парал- лелограмм.
3. Зáданный вектор
3.6. Проекция вектора на оси координат
cх — это проекция вектора c у — это проекция вектора a — это угол между вектором b — это угол между вектором
Так как
(рис.13, а), то
На рис.13, б:
c у — это графическое изображение проекции вектора Найдём проекции вектора 1. Разложим вектор
2. Проекция вектора
cх < 0, если 3. Проекция вектора cу >0, если су < 0, если
Рассмотрим частные случаи
а б а б Рис. 15 Рис. 16
Так как вектор Так как вектор Так как вектор Так как вектор
Можно решить обратную задачу: если мы знаем проекции вектора, то мы можем найти сам вектор, т. е. найти модуль вектора и направление вектора (рис. 17). Модуль вектора
Направление вектора
Или из рис. 17 следует:
Зачем нам нужно знать проекции вектора? Так как проекции векторов на оси координат — это скалярные величины, мы можем заменить любое векторное равенство (уравнение) системой скалярных равенств (уравнений). При этом геометрические действия с векторами мы заменяем алгебраическими действиями с проекциями векторов.
??? ОТВЕТЬТЕ НА ВОПРОСЫ: 1. Какие векторные величины вы знаете? 2. Какие скалярные величины вы знаете? 3. В каком случае модуль результирующего вектора равен: а) сумме модулей составляющих векторов? б) разности модулей составляющих векторов? 4. Можно ли сказать, что
5. В каком случае проекция вектора на ось координат: а) положительная величина? б) отрицательная величина? в) равна нулю? г) равна модулю вектора со знаком «+»? д) равна модулю вектора со знаком « - »?
МЕХАНИКА
Механика изучает механическое движение. М е х а н и ч е с к о е д в и ж е н и е — это процесс изменения положения тела относительно другого тела, которое мы условно считаем неподвижным и называем телом отсчёта. Ⅰ. КИНЕМАТИКА К и н е м a т и к а — это часть механики, которая изучает механическое движение, но не учитывает причины, вызывающие это движение. Задача кинематики ¾ ввести физические величины, которые характеризуют механическое движение и установить соотношения между ними.
1. ОСНОВНЫЕ ПОНЯТИЯ И ХАРАКТЕРИСТИКИ КИНЕМАТИКИ
Мы изучаем движение материальной точки.
1.1. Материальная точка
М а т е р и а л ь н а я т о ч к а — это физическое тело, форму и размеры которого мы можем не учитывать в данной задаче. Например: Земля движется вокруг Солнца. Размеры Солнца и Земли меньше, чем расстояние между Солнцем и Землёй. В этом случае мы можем считать, что Солнце и Земля — материальные точки.
1.2 . Траектория Т р а е к т о р и я — это линия, которую описывает материальная точка при движении (рис. 18).
а б Рис. 18
Эта траектория (рис. 18, а) — кривая линия. Движение материальной точки к р и в о л и н е й н о е. Эта траектория (рис. 18, б) — прямая линия. Движение материальной точки п р я м о л и н е й н о е.
1.3. Путь П у т ь — это скалярная, всегда положительная физическая величина, которая равна длине траектории. Путь обозначается буквой S (читаем «эс»). Путь измеряется в единицах длины. Единица пути в СИ: [S] = 1 м. Единица пути в системе СГС: [S] = 1 см. Внесистемная единица пути: [S] = 1 км. 1.4. Время Время — скалярная физическая величина. Момент времени обозначается символом t. Интервал времени — это разность между двумя моментами времени. Интервал времени обозначается символом Δt (читаем «дельта тэ»): Δt = t– t0, где t — это любой момент времени, t0 — это начальный момент времени. Единица времени в СИ и в системе СГС [t] = l с.
1.5. Тело отсчёта
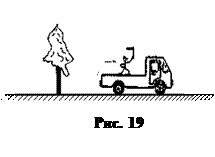
По дороге движется автомобиль, в котором находится человек (рис. 19). В о п р о с: движется или не движется человек? О т в е т: — человек движется относительно дерева (дерево — это тело отсчёта); — человек не движется (находится в покое) относительно автомобиля (автомобиль — это другое тело отсчёта). Мы видим, что человек движется относительно одного тела отсчёта (дерева) и не движется относительно другого тела отсчёта (автомобиля). С д е л а е м в ы в о д: движение и покой — относительные состояния.
1.6. Система координат Мы определяем положение материальной точки её координатами в выбранной нами с и с т е м е к о о р д и н а т (рис. 20). Точка О — это начало координат.
Положение точки на прямой линии определяет одна координата (см. рис. 20, а).
Положение точки на плоскости определяют две координаты (см. рис. 20, б). Положение точки в пространстве определяют три координаты (см. рис. 20, в).
Мы изучаем движение тела в системе отсчёта (рис. 21). Система отсчёта — это тело отсчёта + система координат, связанная с телом отсчёта + секундомер. Тело отсчёта нужно, чтобы определить, движется данное тело или находится в покое в данной системе отсчёта. Система координат нужна для определения положения тела относительно тела отсчёта. Секундомер (часы) — это прибор для измерения времени.
1.8. Радиус-вектор 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Ф и з и ч е с к а я в е л и ч и н а — это характеристика физического тела, физического процесса, физического явления.
Ф и з и ч е с к а я в е л и ч и н а — это характеристика физического тела, физического процесса, физического явления. Пример (рис. 2). Это автобус. Автобус движется.
Пример (рис. 2). Это автобус. Автобус движется.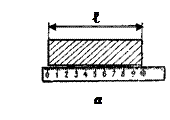 Как мы можем найти физическую величину? Физическую величину мы можем измерить.
Как мы можем найти физическую величину? Физическую величину мы можем измерить.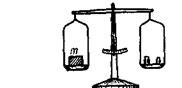 Время t мы измеряем секундомером (рис. 3, в). Секундомер (часы) — это прибор для измерения времени.
Время t мы измеряем секундомером (рис. 3, в). Секундомер (часы) — это прибор для измерения времени. Физическую величину мы можем найти по формуле.
Физическую величину мы можем найти по формуле. Длину ℓ, ширину b, толщину d мы измеряем линейкой.
Длину ℓ, ширину b, толщину d мы измеряем линейкой.
 .
. 1кг/м3 (один килограмм на кубический метр).
1кг/м3 (один килограмм на кубический метр).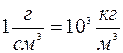
 2.2. Векторные величины
2.2. Векторные величины ,
, ,
, — вектор силы обозначается символом
— вектор силы обозначается символом  .
. ½ или υ — модуль вектора
½ или υ — модуль вектора 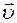 ,
, — модуль вектора
— модуль вектора 
 Математические действия с векторными величинами — это действия векторной алгебры.
Математические действия с векторными величинами — это действия векторной алгебры. (рис. 7).
(рис. 7).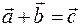 .
. — это результирующий вектор.
— это результирующий вектор.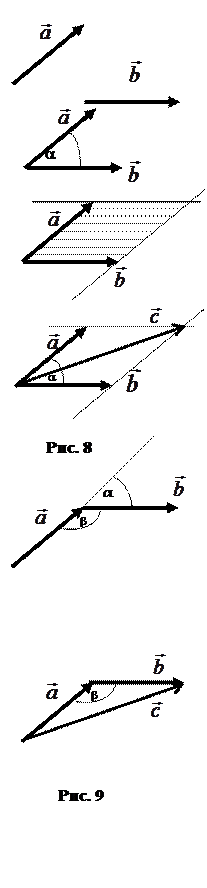
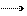
 Правило параллелограмма для сложения двух векторов:
Правило параллелограмма для сложения двух векторов:
 =
= 
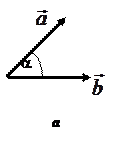 3.3. Вычитание векторов
3.3. Вычитание векторов
 . В этом выражении
. В этом выражении Модуль вектора разности определяется по формуле
Модуль вектора разности определяется по формуле 

 Мы можем найти (изобразить) вектор разности геометрически по правилу параллелограмма или по правилу треугольника (рис. 10).
Мы можем найти (изобразить) вектор разности геометрически по правилу параллелограмма или по правилу треугольника (рис. 10). Вариант 1. Если начало уменьшаемого вектора (вектора
Вариант 1. Если начало уменьшаемого вектора (вектора  3.4. Умножение вектора на скаляр
3.4. Умножение вектора на скаляр

 Начала векторов
Начала векторов  П р о е к ц и я в е к т о р а н а о с ь — это скалярная величина, равная произведению модуля вектора на косинус угла между направлением вектора и положительным направлением оси (рис. 13, а):
П р о е к ц и я в е к т о р а н а о с ь — это скалярная величина, равная произведению модуля вектора на косинус угла между направлением вектора и положительным направлением оси (рис. 13, а):
 и
и
 и
и 
 cх — это графическое изображение проекции вектора
cх — это графическое изображение проекции вектора  и
и 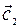 ;
; — составляющий вектор по оси ОХ;
— составляющий вектор по оси ОХ; cх >0, если
cх >0, если 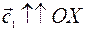 (рис. 14, а; рис. 14, г);
(рис. 14, а; рис. 14, г); (рис. 14, б; рис. 14, в).
(рис. 14, б; рис. 14, в). (рис. 14, а; рис. 14, в)
(рис. 14, а; рис. 14, в) (рис. 14, б; рис. 14, г)
(рис. 14, б; рис. 14, г)


 и
и  (рис. 15, а), то cу = +с и cх = 0
(рис. 15, а), то cу = +с и cх = 0 и
и  и
и 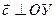 (рис. 16, а), то cх = +с и cу = 0
(рис. 16, а), то cх = +с и cу = 0





 .
. ;
;  ;
; 
 ;
;  ;
; 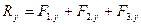 Проекция вектора разности на данную ось равна разности проекций уменьшаемого и вычитаемого векторов на эту же ось.
Проекция вектора разности на данную ось равна разности проекций уменьшаемого и вычитаемого векторов на эту же ось.
 ;
;  ;
; 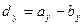
 , если:
, если:

 ,
,  ,
,  ?
?


 Т е л о о т с ч ё т а — это тело, относительно которого мы рассматриваем движение данного тела.
Т е л о о т с ч ё т а — это тело, относительно которого мы рассматриваем движение данного тела.
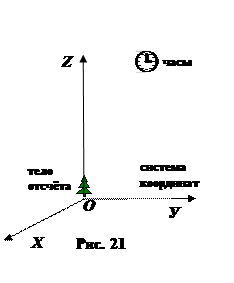 1.7. Система отсчёта
1.7. Система отсчёта