
|
|
Интерполяционнные полиномы Стирлинга, Бесселя, НьютонаИнтерполяционный полином (многочлен) в общем виде:
На практике редко требуется применять полиномы больше 4-й степени. Вопрос сводится к вычислению коэффициентов
Тогда
Приравняем значения полинома [13] при соответствующих значениях t и узлов таблицы
Таблица 4 Уравнения для определения коэффициентов полиномов
Каждая запись может рассматриваться как уравнение для определения коэффициентов A1, A2, A3, A4. Различные интерполяционные формулы получаются в зависимости от того, какие именно выбираются уравнения для определения этих коэффициентов. Если использовать только центральные разности, то
Поэтому интерполяционный многочлен
раскрывая скобки и располагая слагаемые по разностям D:
Это интерполяционный полином Стирлинга.
Пример Пусть требуется вычислить значение x при t=0.05 по формуле Стирлинга. h=0.1, примем t0=0, поэтому
Пусть t – промежуточное, то есть не содержащееся в таблице значение аргумента. t0 – табличное значение аргумента, которое меньше всего отличается от заданного t. Поэтому
В таблице 2 возьмем 4 уравнения, расположенные в строке 0-й и 1-й и между ними. Введем обозначения
Для нахождения коэффициентов A1, A2, A3, A4 используем только разности
Отсюда получаем
Подставляя эти коэффициенты в интерполяционный полином [13] и располагая слагаемые по разностям D:
Это интерполяционный полином Бесселя.
Пример Пусть требуется вычислить значение x при
В таблице 2 возьмем 4 уравнения, расположенные по нисходящей, а именно
Подставляя эти коэффициенты в интерполяционный полином [13]
Это интерполяционный полином Ньютона для интерполирования вперед.
Пример Требуется вычислить значение x при t=-0.25. По формуле Бесселя или Стирлинга нужное вычисление провести нельзя, поскольку на краю таблицы невозможно образовать необходимые для этого разности. В начале таблицы можно легко получить разности, используемые в формуле Ньютона для интерполирования вперед.
h=0.1, примем t0=-0,3, поэтому
В таблице 2 возьмем 4 уравнения, расположенные по восходящей, а именно
Это интерполяционный полином Ньютона для интерполирования назад.
Пример Требуется вычислить значение x при t=0.29. h=0.1, примем t0=0,3, поэтому
Замечания о применении интерполяционных формул. Если заданное значение аргумента находится вблизи начала таблицы, то применять можно только формулу Ньютона для интерполирования вперед, поскольку для других формул потребуется знание узлов таблицы, предшествующих начальному. Аналогично, можно использовать только формулу Ньютона для интерполирования назад, если заданное значение аргумента находится в конце таблицы. Если же заданное значение лежит внутри таблицы, то можно выбрать любую формулу. Критерием выбора интерполяционной формулы может служить величина коэффициентов при разностях последовательных порядков. при заданном Правила применения формул точечной интерполяции: 1. Выбираем начальное значение t0 так, чтобы 2. Составляем таблицу разностей и по порядку разностей, остающимися приблизительно постоянными, определяем степень интерполяционного полинома. 3. Вычисляем последовательные члены выбранной формулы до тех пор, пока они влияют на результат. Если в таблице m значащих цифр, то последовательные члены считают с m+1 знаком. Лишний знак учитывается при сложении и отбрасывается после вычисления суммы с округлением.
Интерполяционные формулы могут быть использованы не только для определения значений функции, соответствующих промежуточным аргументам, которые отсутствуют в таблице, но и для нахождения значений функции, соответствующих аргументам за пределами узловых точек, то есть для экстраполяции. Экстраполяцию обычно проводят с применением формул Лагранжа или Ньютона. Полиномы Бесселя и Стирлинга с центральными разностями предназначены для интерполяции в середине таблице, и поэтому применять их для экстраполяции нецелесообразно. Экстраполяция дает бóльшие ошибки, чем интерполяция и применять ее надо весьма острожно не выходя далеко за пределы крайних узловых точек. Нами рассмотрена прямая табличная задача – отыскание значения функции, соответствующих данным значениям аргумента. Между тем иногда приходится встречаться с обратной табличной задачей интерполяции: по таблице функции x отыскать значение аргумента t, которому соответствует данное значение функции. Задачу обратной интерполяции можно легко решить, поменяв местами аргумент и функцию и сочтя значения функции значениями аргумента, и наоборот. Однако так как разности функции не постоянны, то обратная интерполяция приводит к необходимости построения новой таблицы разностей, новые значения аргумента в которой не являются равноотстоящими.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 [12]
[12]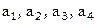 . Введем новую независимую переменную – нормированный аргумент
. Введем новую независимую переменную – нормированный аргумент  :
: и [12] можно записать так
и [12] можно записать так
 [13]
[13] , тогда
, тогда ,
, ,
, ,
, ,
,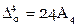 , отсюда получим
, отсюда получим  ,
, ,
, ,
,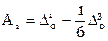 ,
, .
. ,
, ,
,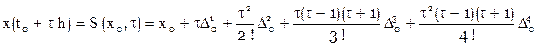 . [14]
. [14] ,
,
 . Если
. Если  , то говорят об интерполяции вперед (от начального значения). Интерполяция в случае
, то говорят об интерполяции вперед (от начального значения). Интерполяция в случае  называется интерполяцией назад, а в случае
называется интерполяцией назад, а в случае  имеем интерполяцию на середину.
имеем интерполяцию на середину.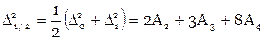 ,
,  .
.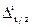 :
:  ,
,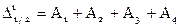 ,
,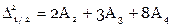 ,
, ,
, .
. ,
,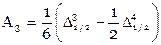 ,
,
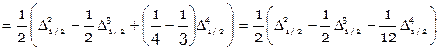 ,
,
 ,
,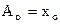 .
.
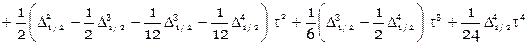 ,
,
 ,
,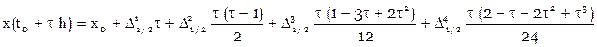
 [15]
[15] по формуле Бесселя.
по формуле Бесселя. , примем
, примем  , поэтому
, поэтому  ,
,
 . Определяя A1, A2, A3, A4:
. Определяя A1, A2, A3, A4: ,
, ,
,
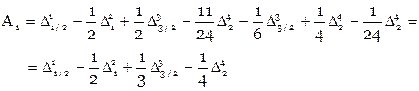
 .
.
 ,
,


 [16]
[16] ,
,
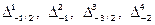 . Определяя A1, A2, A3, A4 и проведя совершенно аналогичные преобразования, получим
. Определяя A1, A2, A3, A4 и проведя совершенно аналогичные преобразования, получим [17]
[17] ,
,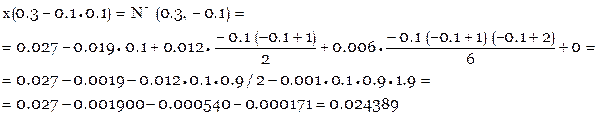
 лучше та формула, которая дает меньшие коэффициенты при разностях, так как при этом уменьшаются ошибки округлений в таблице и в разностях. Сравнение коэффициентов при
лучше та формула, которая дает меньшие коэффициенты при разностях, так как при этом уменьшаются ошибки округлений в таблице и в разностях. Сравнение коэффициентов при 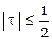 (в других случаях надо выбрать иное начальное значение t0) показывает, что всегда коэффициенты формул Ньютона не меньше коэффициентов двух других формул, а иногда и больше них.
(в других случаях надо выбрать иное начальное значение t0) показывает, что всегда коэффициенты формул Ньютона не меньше коэффициентов двух других формул, а иногда и больше них. и вычисляем
и вычисляем