
|
|
Контроль составления нормальных уравненийСоставление нормальных уравнений надо контролировать. В каждом условном уравнении образуем сумму sk коэффициентов при всех неизвестных и свободного члена; sk есть сумма элементов k–й строки расширенной матрицы коэффициентов.
Получим m сумм
или в обозначениях Гаусса
а это сумма коэффициентов и свободного члена 1-го нормального уравнения! Итак
Поэтому для проверки составления нормальных уравнений следует проделать следующее: 1. просуммировать коэффициенты и свободный член каждого условного уравнения (найти sk) 2. найти сумму произведений коэффициентов 1-го столбца на суммы sk 3. найти суммы коэффициентов и свободного члена 1-го нормального уравнения 4. суммы, найденные в п.2 и п.3 должны совпадать. Аналогично поступаем для проверки составления 2-го, 3-го и т.д. нормальных уравнений.
… … … … … …
контроль k-й строки При умножениях и сложениях надо сохранять все знаки, какие формально получаются при действиях с приближенными числами. Тогда контрольные равенства должны удовлетворяться точно.
Пример Проведем контроль составления нормальных уравнений предыдущего примера.
условные уравнения s
1255 34
нормальные уравнения (суммы коэфф и св члена)
Метод наименьших квадратов в описанном виде применяется только к линейным уравнениям. Одной из задач этого метода является приведение уравнений к линейному виду относительно неизвестных.
Пусть из наблюдений получена совокупность значений xi и yi и известно, что значения связаны функцией
Методом наименьших квадратов решается система
… … … …
Пусть из наблюдений получена совокупность значений xi и yi и известно, что значения yi удовлетворяют нормальному закону распределения вероятности Гаусса. Найти коэффициенты в формуле распределения Гаусса
введем обозначения
тогда получим систему условных уравнений:
Пример Из наблюдений получено
Вычисляем
Составляем условные уравнения (
Нормальные уравнения
Их решение: отсюда Итак
Если случайные ошибки измерений Если вычислена сумма квадратов невязок
ИНТЕРПОЛИРОВАНИЕ При исследовании явлений природы с помощью математического аппарата используются различные функции. Функции могут задаваться различными способами. Простейший из них – задание аналитического выражения, которое дает возможность по любым допустимым значениям аргумента вычислить значение функции. На практике такие случаи бывают весьма редко. Часто функции определяются бесконечными рядами. Вычисление значений функции с помощью бесконечного ряда – довольно громоздкая операция, требующая сходимости и достаточного количества членов ряда. Функция может быть представлена неопределенным интегралом или дифференциальным уравнением. Во всех случаях, когда значения функции либо невозможно точно вычислить, либо вычисление слишком громоздко, прибегают к составлению таблиц функции, если эта функция встречается в различных задачах. Таким образом, мы приходим к табличному заданию функции, то есть такому, когда функция
Табличные значения функции и аргумента называют узлами таблицы. Разность двух соседних значений аргумента называется шагом таблицы Обычно таблица располагается так, что аргумент (например, время) возрастает. При решении задач естествознания, как правило, приходится иметь дело со случаями, когда нужны значения функции не только для табличных значений аргумента (узлов). Так, например, часто требуется знать координаты Солнца относительно Земли, но почти всегда не в 0h Всемирного времени, как дается в Астрономическом ежегоднике, а в определенные промежуточные моменты. Поэтому имеет большое практическое значение следующая задача: дана табличная функция; необходимо найти способ приближенного определения значений функции для произвольных значений аргумента, не совпадающих с узлами таблицы.
Интерполирование по табличной функции сводится к приближению табличной функции другой, легко вычисляемой функцией. Выражение для этой легко вычисляемой функции используется для интерполяции: заданное значение аргумента подставляется в нее и производятся вычисления. Построение приближения табличной функции представляет неопределенную задачу и требует дополнительных соглашений. Во-первых, надо условиться относительно класса функций, используемых для приближения. Очевидно, желательна возможность легкого вычисления функции по заданному значению аргумента. Этому условию удовлетворяют алгебраические полиномы, которые чаще всего и используются для приближения. Если табличная функция периодическая и приближение нужно в области, охватывающей весь период, то используют тригонометрические полиномы. Когда периодическую функцию нужно приблизить только на небольшой части периода, то обычно используют алгебраические полиномы. Во-вторых, надо потребовать, чтобы приближение было возможно лучшим. Что значит «лучшим»? На практике употребляют различные критерии наилучшего приближения. Мы примем такой: приближающий полином, который должен точно представлять узлы таблицы. То есть интерполяционный полином должен на графике пройти через все точки (узлы) табличной функции. По этой причине интерполяция с указанным условием называется точечной интерполяцией.
Если за 24 часа величина Х изменяется равномерно на D, то ее значение для момента t часов, прошедших после момента t0 равно
Но такого практически никогда не бывает, разность соседних значений в таблице изменяется, и иногда сложным образом. Можно допустить линейное интерполирование, если не требуется большой точности. Но если надо получить значение табличной функции с той же точностью, что и в узлах, то, согласно принятым соглашениям, надо строить интерполяционный полином. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 . Далее вычисляем сумму произведений по столбцам системы условных уравнений и подставляем значение sk
. Далее вычисляем сумму произведений по столбцам системы условных уравнений и подставляем значение sk
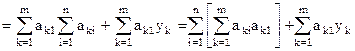
 ,
, .
.
 s1 m>n
s1 m>n s2
s2 s3
s3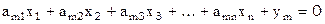 sm
sm



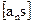








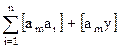

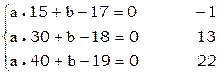

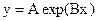 . Найти наилучшие A и B.
. Найти наилучшие A и B.


 , где
, где 

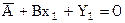

 относительно
относительно  . Окончательно
. Окончательно  .
. .
.





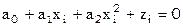 , решая которую методом наименьших квадратов получим
, решая которую методом наименьших квадратов получим  , из которых найдем параметры нормального распределения
, из которых найдем параметры нормального распределения 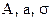 .
. ,
, 
 ):
):













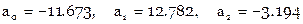
 ,
,  ,
,  .
.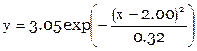 .
. удовлетворяют нормальному закону распределения, то применение принципа Лежандра дает наиболее вероятные значения неизвестных.
удовлетворяют нормальному закону распределения, то применение принципа Лежандра дает наиболее вероятные значения неизвестных. , то средняя погрешность одного условного уравнения s:
, то средняя погрешность одного условного уравнения s: , (m – число уравнений, n – число неизвестных) [6]
, (m – число уравнений, n – число неизвестных) [6] вычисляют еще и для того, чтобы найти грубо ошибочные условные уравнения (если они есть). Если какое-либо
вычисляют еще и для того, чтобы найти грубо ошибочные условные уравнения (если они есть). Если какое-либо  , то вероятно в соответствующем условном уравнении есть грубая ошибка, такие уравнения отбрасывают. После это заново составляют нормальные уравнения и повторяют решение.
, то вероятно в соответствующем условном уравнении есть грубая ошибка, такие уравнения отбрасывают. После это заново составляют нормальные уравнения и повторяют решение.

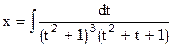
 определяется таблицей своих значений
определяется таблицей своих значений  при заданных значениях аргументов
при заданных значениях аргументов  , i=1,2,…n:
, i=1,2,…n: . Если эта разность изменяется, то таблица называется таблицей с переменным шагом, если разность неизменна, то это таблица с постоянным шагом. Стараются строить таблицы с постоянным шагом. Шаг, вообще говоря, не может быть очень малым, иначе сильно возрастает объем таблицы.
. Если эта разность изменяется, то таблица называется таблицей с переменным шагом, если разность неизменна, то это таблица с постоянным шагом. Стараются строить таблицы с постоянным шагом. Шаг, вообще говоря, не может быть очень малым, иначе сильно возрастает объем таблицы. Если значение аргумента задано внутри области табличных значений аргумента, то указанную задачу называют задачей интерполяции; если же значение аргумента задано вне табличной области, то говорят об экстраполяции.
Если значение аргумента задано внутри области табличных значений аргумента, то указанную задачу называют задачей интерполяции; если же значение аргумента задано вне табличной области, то говорят об экстраполяции. Если какая-либо величина изменяется пропорционально времени, то разность значений через равные промежутки времени постоянна. В этом случае, можно применить простейшее линейное интерполирование.
Если какая-либо величина изменяется пропорционально времени, то разность значений через равные промежутки времени постоянна. В этом случае, можно применить простейшее линейное интерполирование. .
.