
|
|
Интерполяционный полином Ньютона для таблицы с переменным шагомИнтерполирование по формуле Лагранжа подразумевает, что множество используемых узлов таблицы наперед известно. Но обычно известна лишь требуемая точность, а множество узлов, которые надо использовать зависит от вида табличной функции и способа интерполирования. Вычисления по формуле Лагранжа достаточно громоздки, и если потребуется увеличить количество используемых узлов таблицы для того же аргумента t, то придется повторить все вычисления заново. Интерполяционная формула Ньютона, которая будет изложена ниже, представляет собой просто другой способ написания интерполяционного полинома (это так называемая разностная интерполяционная формула). В этом способе расчеты не так громоздки, а количество используемых узлов таблицы может быть легко увеличено или уменьшено без повторения всех вычислений. Пусть так же как в предыдущем рассмотрении в виде дух столбцов дана таблица значений функции Разделенной разностью 1-го порядка двух табличных значений называется отношение разности значений функции к разности соответствующих значений аргумента. Обозначения разделенных разностей строятся так, чтобы были указаны взятые табличные значения аргумента. Так
Разделенной разностью 2-го порядка трех табличных значений называется отношение разности двух разделенных разностей 1-го порядка к разности крайних значений аргумента.
Аналогично определяются разделенные разности любого порядка, например, разности 3-го порядка
Таблица разделенных разностей
Если имеется n значений узлов таблицы, то можно построить n-1 разность 1-го порядка, n-2 разности 2-го порядка, и только одну разность n-1 порядка. Значения функции в узлах таблицы иногда называют разделенными разностями 0-го порядка. Пример Построим таблицу разделенных разностей для функции
По заданной таблице Условие точечной интерполяции требует, чтобы искомый полином проходил через все узлы табличной функции
а поскольку задано n узлов таблицы, то имеем n основных уравнений:
Если значения функции
Приравнивая эти 1-е разделенные разности, получим еще n-1 уравнение:
Вспомним из алгебры
Разделенная разность 1-го порядка есть полином n-1 порядка. Аналогично можно показать, что разделенная разность i-го порядка есть полином n–i-го порядка. Разделенная разность n-го порядка есть полином 0-й степени, то есть постоянное число. Разделенные разности порядка большего, чем n, равны 0. Это свойство полинома крайне важно в интерполировании. Табличная функция редко бывает полиномом, но если это так, то после составления таблицы разностей окажется, что разности некоторого порядка – постоянные числа. Но обычно табличная функция – не полином, и строго постоянных разностей не получится. Однако в большинстве задач табличные функции таковы, что они могут быть приближены полиномом некоторой степени. В этих задачах разности некоторого порядка будут почти постоянными, а следующие разности – очень малыми. Тогда можно уверенно применять точечную интерполяцию и строить полином, степень которого равна порядку почти постоянных разностей. Построение таблицы разностей поэтому есть единственный способ выяснить нужную степень интерполяционного полинома, то есть число узлов, необходимое для удовлетворительного приближения.
Допустим, число узлов таблицы равно 3, ограничимся частным случаем, когда степень интерполяционного полинома равна n-1=2.
и так далее. Таблица 2 Таблица разделенных разностей
Из полученных 6 уравнений для определения коэффициентов а0, а1, а2 надо выбрать любые 3. Выберем уравнения в верхней части таблицы:
Подставим эти коэффициенты в формулу [10]
Полученный полином расположим не по степеням t, а по разностям последовательных порядков.
Рассмотрим коэффициент при 3-й разности
Окончательно
Аналогично строится полином при любом числе узлов. Для вычислений удобно представить
В этом случае вычисления выполняются «с конца» : разность 3-го порядка умножается на
Пример Требуется построить интерполяционную формулу и по ней вычислить значение синуса при Воспользуемся предыдущей таблицей разностей для значений синуса при
В таблице подчеркнуты разности, используемые в формуле. Формула для произвольных аргументов t согласно [11’] имеет вид
по таблице значений синусов можно проверить

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 с произвольным шагом аргумента t. В этом случае разность между значениями
с произвольным шагом аргумента t. В этом случае разность между значениями  и
и 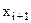 в соседних узлах таблицы не может служить для описания изменения функции. Для этого используются так называемые разделенные разности.
в соседних узлах таблицы не может служить для описания изменения функции. Для этого используются так называемые разделенные разности.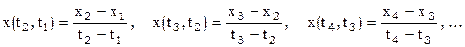

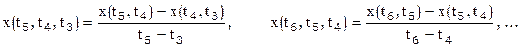
 Таблица 1
Таблица 1 для значений аргумента
для значений аргумента 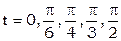 .
.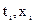 получим теперь выражение для интерполяционного полинома Ньютона n-й степени.
получим теперь выражение для интерполяционного полинома Ньютона n-й степени.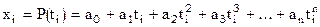 , [10]
, [10] ,
,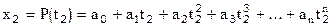 ,
,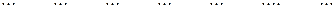
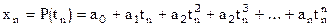 .
. в узлах совпадает, то должны совпадать и их разделенные разности:
в узлах совпадает, то должны совпадать и их разделенные разности:

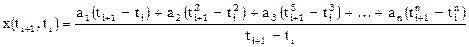 .
.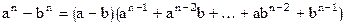 , поэтому дробь можно сократить на
, поэтому дробь можно сократить на  :
:
 ,
,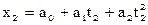 ,
, .
.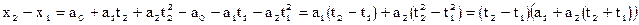 учитывая a2-b2=(a-b)(a+b)
учитывая a2-b2=(a-b)(a+b)
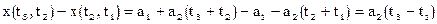 ,
,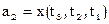 ,
,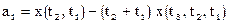 ,
,
 :
: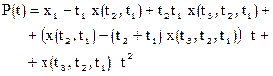


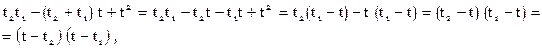
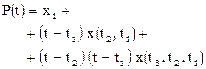 [11]
[11] в следующем виде (с учетом разностей 3-го порядка)
в следующем виде (с учетом разностей 3-го порядка) [11’]
[11’] , к произведению прибавляется разность 2-го порядка, сумма умножается на
, к произведению прибавляется разность 2-го порядка, сумма умножается на  , к произведению прибавляется разность 1-го порядка, сумма умножается на
, к произведению прибавляется разность 1-го порядка, сумма умножается на 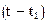 и, наконец, к произведению прибавляется разность нулевого порядка.
и, наконец, к произведению прибавляется разность нулевого порядка.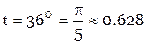 .
. .
.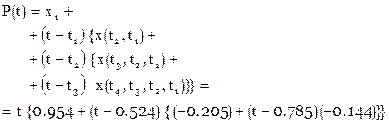
 ,
,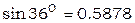 .
.