
|
|
Умножение, деление и вычисление функций от приближенных чиселЕсли приближенное число надо умножить (разделить) на точное (удвоить, утроить и т.д.), то относительная погрешность произведения (частного) равна относительной погрешности приближенного множителя, поэтому в произведении оставляем столько цифр, сколько их в приближенном множителе. Например,
Абсолютная погрешность произведения увеличивается пропорционально точному сомножителю; абсолютная погрешность частного уменьшится пропорционально точному делителю. Если оба сомножителя заданы приближенно, то число верных цифр произведения равно числу верных цифр наименее точного множителя. Если, например, в одном множителе 4 верные цифры, а в другом – только 2, то в произведении можно будет ручаться только за 2 цифры. Например, найдем произведение чисел
Посмотрим, какой результат дадут граничные случаи. Для этого перемножим вначале наименьшие возможные значения А и В, а затем наибольшие и получим для произведения АВ: нижнюю границу верхнюю границу Сравнивая эти два произведения, видим, что после округления в них совпадают только первые три цифры, а остальные шесть найдены лишь для того, чтобы их отбросить. Таким образом, если мы найдем произведение данных приближенных чисел
то в этом результате можно гарантировать надежность только первых трех цифр – ровно столько значащих цифр имеет наименее точное число В=0.0764. В отдельных неблагоприятных случаях даже и последняя из гарантированных цифр может быть сомнительной. Пример. Найдем произведение приближенных чисел
Решение: Действительно, нижними и верхними границами здесь будут произведения
поэтому последняя цифра произведения Подчеркнем также, что при умножении и делении приближенных чисел положение запятой у компонентов совершенно не влияет на точность результата.
Пример
Возведение в степень приближенного числа всегда можно рассматривать как n-кратное умножение этого числа самого на себя, поэтому при возведении в степени относительная погрешность увеличивается пропорционально показателю степени. То есть при возведении в квадрат относительная погрешность удваивается, при возведении в куб – утраивается, и т.д. При извлечении корня всегда получаем не меньшее количество значащих цифр, чем то, которое имеется в подкоренном выражении:
Чтобы уменьшить накопление ошибок округления при вычислениях, на всех промежуточных этапах следует сохранять не только верные, но и несколько сомнительных знаков. Иными словами, выделять из полученного числа верные знаки следует только в итоге всех вычислений.
Контроль вычислений Каждое вычисление выполняется по разработанному алгоритму (Алгоритмом называется совокупность математических операций, которые следует выполнить в определенном порядке, для того что бы решить задачу данного типа). Алгоритм может быть задан формулами или словесными или символическими правилами по которым выполняется вычисление. Никогда не следует пользоваться отдельными клочками бумаги для записи вспомогательных данных – результатом будет напрасная трата времени из-за их утери и увеличение количества ошибок и описок. Все вычисления записываются в единой системе. Цифры надо писать аккуратно, так как практика показывает, что небрежно записанные цифры часто ошибочно принимают за другие. Исправляют неправильный результат зачеркивая его и проставляя сверху правильные цифры, но так, чтобы при надобности зачеркнутые цифры можно было прочесть. Непременной частью вычислений является их контроль. Непроверенный результат вычислений ненадежен, и пока не осуществлен контроль, вычисления нельзя считать оконченными. Контроль надо начинать с проверки правильности исходных данных и расчетных формул. Повторное вычисление по тем же самым формулам не гарантирует от повторения ошибок, поэтому более надежный контроль достигается вычислением по другим формулам или при помощи решения обратной задачи (умножение проверяется делением и т.д.) Сложные вычисления надо разбивать на ряд более простых этапов и переходить к каждому новому этапу только после контроля результатов предыдущего этапа. Самые надежные результаты дает новое вычисление, выполненное независимо другим вычислителем, если возможно, по другим расчетным формулам.
О ПОСТРОЕНИИ ГРАФИКОВ 1. Надписи и подписи должны содержать целостную информацию о содержании графика или рисунка. Иными словами, для того, чтобы понять, что изображено, не надо было бы дополнительно обращаться к тексту или задавать вопросы. На осях должны быть указаны единицы измерения и подписаны числовые значения изображенных величин. Если в одной области построения изображено несколько графиков, то надо добавить легенду, то есть пояснить, что именно показано на каждом графике. 2. Шаг делений осей должен быть не слишком малым, иначе это приведет к густому «частоколу» делений; и не слишком большим, иначе нельзя будет ориентироваться в величинах представленной информации. 3. График должен по возможности занимать всю полезную площадь области построения. Для этого надо верно выбрать положение начала отсчета и масштаб величин на осях графика. 4. Все надписи и подписи должны быть выполнены на одном языке.
СГЛАЖИВАНИЕ Численное значение физической величины получается в результате ее измерения, то есть сравнения ее с другой величиной, принятой за единицу. Это эмпирические данные. При достаточно точных измерениях одной и той же величины результаты отдельных измерений отличаются друг от друга, и, следовательно, содержат ошибки. Выше эти ошибки мы назвали ошибками в исходной информации. Ошибкой измерения называется разность х–а между результатом измерения х и истинным значением а измеряемой величины (модуль ошибки это абсолютная погрешность). Ошибка измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Одной из основных задач математической обработки результатов измерений является оценка истинного значения измеряемой величины. Другими словами, после неоднократного измерения величины а и получения ряда результатов, каждый из которых содержит некоторую неизвестную ошибку, ставится задача вычисления приближенного значения а с возможно меньшей ошибкой. Грубые ошибки (промахи) – возникают вследствие нарушения основных условий измерения или в результате недосмотра экспериментатора (при измерении длины начало линейки по недосмотру не было совмещено с началом отрезка; при плохом освещении вместо «3» записывают «8»). При обнаружении грубой ошибки результат измерения отбрасывают, а само измерение по возможности повторяют. Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от результатов остальных измерений. Систематические ошибки – возникают по причинам, эффект воздействия которых может быть рассчитан. Например, после измерений обнаружена неправильная регулировка прибора, которая привела к смещению начала отсчета. Из-за этого все снятые показания оказались смещены на постоянную величину (торговые весы). Другим примером может служить изменение внешних условий, если известно влияние этих изменений на результаты измерений (изменение температуры при наблюдениях с учетом рефракции). Как только систематические ошибки обнаружены и их величины рассчитаны, они легко устраняются путем введения соответствующих поправок в измерения. Случайные ошибки – вызываются большим количеством таких факторов, воздействие которых столь незначительны, что их нельзя выделить и учесть в отдельности (при данном уровне техники и точности измерений). Например, в перекрестье нитей окуляра наблюдается звезда, ее положение смещается из-за мерцания (рефракции), случайных изменений температуры вблизи телескопа, деформаций линз и самой трубы, волновой природы света, колебаний почвы под телескопом и т.д. Случайную ошибку можно рассматривать как суммарный эффект действия таких факторов. Случайные ошибки являются неустранимыми, их нельзя устранить в каждом из результатов измерений, но можно оценить их величину. В дальнейшем будем полагать, что грубые и систематические ошибки измерений уже исключены из результатов измерений. Для многих задач анализа наблюдений (дифференцирования, интегрирования) важно смягчить влияние случайных ошибок. Для этой цели применяют сглаживание эмпирических данных, то есть заменяют таблицу, полученную из наблюдений, таблицей близких к ним точек, лежащих на достаточно гладкой кривой. Сглаживание производится с помощью многочленов оптимального порядка. Мы рассмотрим только сглаживание многочленом первой степени – линейное сглаживание – по таблице с постоянным шагом.
формулы линейного сглаживания по 5-м точкам:
Здесь приняты следующие обозначения: средней точке группы приписывается индекс 0, симметричные точки получают при этом индексы ±1, ±2,… Сглаженные значения обозначаются волнистой чертой сверху. О достаточной гладкости таблицы можно судить по табличным разностям (значение минус предыдущее значение), которые должны изменяться плавно. Иногда применяют повторное сглаживание. Отметим, что результат сглаживания существенно зависит от применяемого метода сглаживания, выбор которого подсказывается обычно интуицией. Описанный процесс сглаживания иногда еще называют фильтрацией. В данном случае мы применили линейное сглаживание или линейный фильтр. Математические фильтры удаляют из функции некоторые частоты, примерно так как масляный фильтр удаляет из жидкости частицы определенных размеров. Теория построения фильтров очень развита.
АППРОКСИМАЦИЯ Измеренные значения физической величины очень удобно представить уравнением, связывающим независимую величину - аргумент (например, время) и значение физической величины (например, температуру). В этом случае говорят о подборе эмпирической формулы. Предположим, в виде таблице задана зависимость x(t):
Несомненные удобства представляет знание функциональной зависимости Итак, аппроксимация это замена аналитически не выражаемой функции через аналитически вычисляемую функцию по возможности более точно.
СПРЯМЛЕНИЕ (ЛИНЕАРИЗАЦИЯ) Сравнение небольшого числа точек на графике f(x) с аналитической кривой весьма затруднительно. Поэтому кривую f(x) линеаризуют, преобразуя масштаб по обеим осям. После этого сравнивают отдельные точки с прямой линией. Если они лежат на прямой, то график f(x) может совпадать с аналитической кривой. Спрямлением или линеаризацией называется преобразование эмпирической формулы вида Применение этого метода рассмотрим на примерах часто встречающихся зависимостей. Для преобразования к линейному виду степенной функции
Аналогично
Пример Из наблюдений получена таблица изменения x (t):
Очевидно, точки на прямую не укладываются. Предположим, что эту зависимость можно описать дробной функцией  . Проведем спрямление. . Проведем спрямление.
График – не прямая, поэтому дробная зависимость выбрана неверно.
Предположим, что эту зависимость можно описать экспонентой:
График – прямая, поэтому экспоненциальная зависимость выбрана верно.
Отметим, что таким способом линеаризация зависимостей вида
Продолжим рассмотрение примера. Способ спрямления зависимости показал, что ее можно представить в виде аналитической функции вида
легко записать уравнения для нахождения этих коэффициентов
Требуется найти 2-а неизвестных A и B из 5-ти уравнений. Это избыточная система линейных уравнений. Нельзя отбросить «лишние» уравнения, поскольку коэффициенты этих уравнений отягощены ошибками и выбор различных уравнений системы приведет к тому, что их решения будут различаться.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В астрономической практике часто встречаются такие задачи, в которых величины, подлежащие определению, не наблюдаются непосредственно. Вместо них могут быть определены некоторые зависимые величины. Прямое измерение нужных величин заменяется измерением других величин. Например, при определении блеска звезды по фотопластинке измеряется интенсивность потемнения фотоэмульсии. Измерить прямое восхождение звезды на небесной сфере невозможно, для его вычисления измеряют некоторые промежутки времени, в течение которых движется звезда, участвуя в суточном вращении небесной сферы. Еще пример: траектория небесного тела вычисляется по известным начальным условиям и параметрам. Наблюдения обнаруживают некоторую разницу между вычисленными координатами и наблюденными (О-С – observee minus calculee). Если эта разница возникает из-за неточного знания начальных условий и параметров, то ставится задача определения их поправок по величинам О-С. Эта задача всегда решается по способу наименьших квадратов. В общем виде задача ставится так. Имеется n неизвестных параметров x1, x2, x3,…xn. Для каждой группы этих значений из наблюдений получена величина yk.
Если бы при наблюдениях не было случайных ошибок или они были бы пренебрежимо малыми, то достаточно было бы сделать ровно столько наблюдений, сколько неизвестных xi (то есть n), получить уравнения и решить их. Но на практике величины yk содержат случайные ошибки, величинами которых пренебрегать нельзя. Если составить ровно столько независимых уравнений, сколько неизвестных, то эти ошибки целиком войдут в корни системы. Для того, чтобы взаимно компенсировать влияние ошибок, принято брать число наблюдений и, следовательно, число уравнений гораздо большим, чем число неизвестных. Тогда получается своеобразная с алгебраической стороны система уравнений вида
… … … … … …
Здесь m – число уравнений (наблюдений), n – число неизвестных. Эти уравнения получены из наблюдений и называются условными уравнениями. Расширенная матрица коэффициентов системы условных уравнений:
Принцип Лежандра Поскольку в системе [3] уравнений больше чем неизвестных, то не существует таких значений корней x1, x2, x3,…xn которые бы удовлетворяли одновременно всем уравнениям системы. Система [3] несовместна. Иными словами, подстановка любых значений неизвестных, например,
Очевидно, естественно выбрать значения неизвестных Если дана система равноточных условных уравнений, то условимся искать неизвестные так, чтобы сумма квадратов невязок была наименьшей. Это и есть принцип Лежандра. Хотя нельзя обеспечить малость отдельных невязок, но минимальность суммы квадратов обеспечивает ограниченность и отдельных невязок. Иными словами, необходимо найти минимум аналитической функции – суммы квадратов невязок
… … …
[4] – система нормальных уравнений. Для определения неизвестных всегда получается система с числом уравнений, равным числу неизвестных, поэтому задача становится определенной. Для 1-го уравнения системы [4]
Введем обозначения Гаусса
Это система нормальных уравнений. Ее решение соответствует минимуму суммы квадратов невязок
Пример Таблично задана функция
Методом наименьших квадратов найти линейное уравнение, представляющее данные таблицы в виде Здесь неизвестны коэффициенты k и b. Перепишем эту функцию в виде Составляем условные уравнения в виде
Расширенная матрица коэффициентов условных уравнений
Расширенная матрица коэффициентов нормальных уравнений вычисляется так
Итак
Система нормальных уравнений
Возвращаясь к прежним обозначениям
Найдем невязки
Отметим, что
Пример Утром, после восхода Солнца, метеоролог отмечал рост температуры воздуха
Найти формулу, позволяющую вычислить температуру, зная время на интервале с 8 до 9 часов утра в виде T= at+b. Составляем условные уравнения, считая что время отсчитывается в минутах с 8 часов утра.
Расширенная матрица коэффициентов условных уравнений
Расширенная матрица коэффициентов нормальных уравнений
Система нормальных уравнений
2725 a + 85 (18-28.33 a)-1555 = 0, 316.95 a – 25 = 0, a = 0.0789, b = 15.76, Итак, T = 0.0789 t + 15.76
из формулы O-C t = 15m T=17O T=16.94O 0.06 t = 30m T=18O T=18.13O -0.13 t = 40m T=19O T=18.92O 0.08

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. и
и  . В действительности А и В могут быть произвольными числами, лежащими в таких промежутках
. В действительности А и В могут быть произвольными числами, лежащими в таких промежутках ,
,  .
. ;
; .
. ,
, и
и  .
. .
. ;
; ,
, сомнительна и может иметь погрешность, составляющую 5 единиц последнего разряда.
сомнительна и может иметь погрешность, составляющую 5 единиц последнего разряда.

 (нули незначащие)
(нули незначащие) (справа ноль значащий)
(справа ноль значащий) , причем все цифры результата верны, поскольку
, причем все цифры результата верны, поскольку


 Наилучшее сглаживание получается для средних точек, когда учитывается информация о поведении функции по обе стороны от сглаживаемой точки. Поэтому количество точек выбирают нечетным, а группы точек – скользящими вдоль всей таблицы. Берут, например, первые три точки х1, х2, х3 и сглаживают с их помощью среднюю точку х2, затем берут следующую группу х2, х3, х4 и сглаживают точку х3 и т.д. до конца таблицы. При этом, очевидно, остаются несколько крайних точек, которые можно сгладить с меньшей точностью. Формулы линейного сглаживания по 3-м точкам:
Наилучшее сглаживание получается для средних точек, когда учитывается информация о поведении функции по обе стороны от сглаживаемой точки. Поэтому количество точек выбирают нечетным, а группы точек – скользящими вдоль всей таблицы. Берут, например, первые три точки х1, х2, х3 и сглаживают с их помощью среднюю точку х2, затем берут следующую группу х2, х3, х4 и сглаживают точку х3 и т.д. до конца таблицы. При этом, очевидно, остаются несколько крайних точек, которые можно сгладить с меньшей точностью. Формулы линейного сглаживания по 3-м точкам: , [1]
, [1] (в начале таблицы),
(в начале таблицы), (в конце таблицы);
(в конце таблицы); , [2]
, [2] ,
,  (в начале),
(в начале), ,
,  (в конце).
(в конце).
 . В данном случае зависимость близка к степенной и представима функцией
. В данном случае зависимость близка к степенной и представима функцией  . Обычно можно найти такую функцию, график которой проходит очень близко от заданных таблицей значений. Поиск такой аналитической функции, которая дает наилучшее представление табличных данных, составляет основную задачу аппроксимации.
. Обычно можно найти такую функцию, график которой проходит очень близко от заданных таблицей значений. Поиск такой аналитической функции, которая дает наилучшее представление табличных данных, составляет основную задачу аппроксимации. к виду
к виду  путем надлежащей замены переменных.
путем надлежащей замены переменных. применяется логарифмическое преобразование:
применяется логарифмическое преобразование:
 ,
,  :
: ,
, 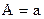 ,
, 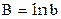 ,
,  ,
,  .
.
 ,
,  :
: ,
,  ,
,  ,
,  ,
, 
 ,
,  :
: ,
, 
 :
: ,
,  ,
,  ,
, 
 :
: ,
,  ,
, 
 ,
,  :
: ,
,  ,
,  ,
,  ,
, 
 :
: ,
, 
 . Проведем спрямление.
. Проведем спрямление.
 или
или  невозможна.
невозможна. или
или  ,
, или
или  ,
, или
или  ,
, или
или  ,
, или
или  .
.



 [3]
[3] m>n
m>n




 даст
даст .
. были бы возможно меньшими.
были бы возможно меньшими. . Необходимые условия минимума этой функции:
. Необходимые условия минимума этой функции:

 [4]
[4]
 ,
, , подставляя значение
, подставляя значение  , получим
, получим ,
, , меняя порядок суммирования в первом слагаемом
, меняя порядок суммирования в первом слагаемом .
. , i=1,n,
, i=1,n, , тогда последнее уравнение примет вид
, тогда последнее уравнение примет вид  или, в развернутом виде
или, в развернутом виде


 [5]
[5]

 .
. . В предыдущих обозначениях с индексами это два неизвестных х1 и х2.
. В предыдущих обозначениях с индексами это два неизвестных х1 и х2.
















 , решая
, решая 
 ,
,
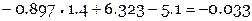


 .
.






 , решая b=18-28.33 a
, решая b=18-28.33 a 0.01
0.01