
|
|
Масштабирование и восстановление данныхВ этом разделе описаны функции масштабирования, препроцессорной обработки
Синтаксис: [pn,minp,maxp,tn,mint,maxt] = premnmx(p,t) [pn,minp,maxp] = premnmx(p) Описание: Функция premnmx выполняет препроцессорную обработку обучающей последовательности путем приведения значений элементов векторов входа и цели к интервалу [–1 1]. Входные аргументы: p – матрица векторов входа размера R´Q; t – матрица векторов целей размера S´Q. Выходные аргументы: pn – матрица нормированных векторов входа размера R´Q; minp – вектор минимальных элементов входа размера R´1; maxp – вектор максимальных элементов входа размера R´1; tn – матрица нормированных векторов целей размера S´Q; mint – вектор минимальных элементов векторов целей размера S´1; maxt – вектор максимальных элементов векторов целей размера S´1. Пример: Следующие команды нормализуют приведенный набор данных так, чтобы значения входа и цели попадали в интервал [–1,1]: p = [–10 –7.5 –5 –2.5 0 2.5 5 7.5 10]; t = [0 7.07 –10 –7.07 0 7.07 10 7.07 0]; [pn,minp,maxp,tn,mint,maxt] = premnmx(p,t) pn = –1.0000 –0.7500 –0.5000 –0.2500 0 0.2500 0.5000 0.7500 1.0000 minp = –10 maxp = 10 tn = 0 0.7070 –1.0000 –0.7070 0 0.7070 1.0000 0.7070 0 mint = –10 maxt = 10 Если требуется нормировать только вектор входа, то можно использовать следующий оператор: [pn,minp,maxp] = premnmx(p); Алгоритм: Приведение данных к диапазону [–1 1] выполняется по формуле pn = 2 * (p – minp)/(maxp – minp) – 1. Сопутствующие функции: PRESTD, PREPCA, POSTMNMX.
Синтаксис: [pn,meanp,stdp,tn,meant,stdt] = prestd(p,t) [pn,meanp,stdp] = prestd(p) Описание: Функция prestd выполняет препроцессорную обработку обучающей последовательности путем приведения значений элементов векторов входа к нормальному закону распределения c нулевым средним и дисперсией, равной 1. Входные аргументы: p – матрица векторов входа размера R´Q; t – матрица векторов целей размера S´Q. Выходные аргументы: pn – матрица приведенных векторов входа размера R´Q; meanp – вектор средних значений векторов входа размера R´1; stdp – вектор среднеквадратичных отклонений векторов входа размера R´1; tn – матрица приведенных векторов целей размера S ´ Q; meant – вектор средних значений векторов целей размера S´1; stdt – вектор среднеквадратичных отклонений векторов целей размера S´1. Пример: Задана следующая обучающая последовательность векторов входа и целей. Требуется выполнить ее приведение к нормальному закону распределения с параметрами [0 1]. p = [–0.92 0.73 –0.47 0.74 0.29; –0.08 0.86 –0.67 –0.52 0.93]; t = [–0.08 3.4 –0.82 0.69 3.1]; [pn,meanp,stdp,tn,meant,stdt] = prestd(p,t) pn = –1.3389 0.8836 –0.7328 0.8971 0.2910 –0.2439 1.0022 –1.0261 –0.8272 1.0950 meanp = 0.0740 0.1040 stdp = 0.7424 0.7543 tn = –0.7049 1.1285 –1.0947 –0.2992 0.9704 meant = 1.2580 stdt = 1.8982 Если задана только последовательность векторов входа, то следует применить оператор [pn,meanp,stdp] = prestd(p); Алгоритм: Приведение данных к нормальному закону распределения с параметрами [0 1] выполняется по формуле pn = (p – meanp)/stdp. Сопутствующие функции: PREMNMX, PREPCA.
Синтаксис: [ptrans,transMat] = prepca(P,min_frac) Описание: Функция prepca выполняет препроцессорную обработку обучающей последовательности, применяя факторный анализ. Это позволяет преобразовать входные данные так, чтобы векторы входа оказались некоррелированными. Кроме того, может быть уменьшен и размер векторов путем удержания только тех компонентов, дисперсия которых превышает некоторое заранее установленное значение min_frac. Входные аргументы: P – матрица центрированных векторов входа размера R´Q; min_frac – нижняя граница значения дисперсии удерживаемых компонентов. Выходные аргументы: ptrans – преобразованный набор векторов входа; transMat – матрица преобразований. Примеры: Зададим массив двухэлементных векторов входа и выполним их факторный анализ, удерживая только те компоненты вектора, дисперсия которых превышает 2 % общей дисперсии. Сначала с помощью функции prestd приведем входные данные к нормальному закону распределения, а затем применим функцию prepca. P = [–1.5 –0.58 0.21 –0.96 –0.79; –2.2 –0.87 0.31 –1.4 –1.2]; [pn,meanp,stdp] = prestd(P) pn = –1.2445 0.2309 1.4978 –0.3785 –0.1058 –1.2331 0.2208 1.5108 –0.3586 –0.1399 meanp = –0.7240 –1.0720 stdp = 0.6236 0.9148 [ptrans,transMat] = prepca(pn,0.02) ptrans = 1.7519 –0.3194 –2.1274 0.5212 0.1738 transMat = –0.7071 –0.7071 Поскольку в данном примере вторая строка массива P почти кратна первой, то в результате факторного анализа преобразованный массив содержит только одну строку. Алгоритм: Функция prepca для выделения главных компонентов использует процедуру SVD-разложения матрицы центрированных векторов входа по сингулярным числам. Векторы входа умножаются на матрицу, строки которой являются собственными векторами ковариационной матрицы векторов входа. В результате получаем векторы входа с некоррелированными компонентами, которые упорядочены по величине дисперсий. Те компоненты, дисперсия которых не превышает заданное значение, удаляются; в результате сохраняются только главные компоненты [22]. Предполагается, что входные данные центрированы Сопутствующие функции: PRESTD, PREMNMX.
Синтаксис: [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt) p = postmnmx(pn,minp,maxp) Описание: Функция postmnmx выполняет постпроцессорную обработку, связанную с восстановлением данных, которые были масштабированы к диапазону [–1 1] с помощью функции premnmx. Входные аргументы: pn – матрица нормированных векторов входа размера R´Q; minp – вектор минимальных элементов исходного массива p размера R´1; maxp – вектор максимальных элементов исходного массива p размера R´1; tn – матрица нормированных векторов целей размера S´Q; mint – вектор минимальных элементов исходного массива t размера S´1; maxt – вектор максимальных элементов исходного массива t размера S´1. Выходные аргументы: p – восстановленная матрица векторов входа размера R´Q; t – восстановленная матрица векторов целей размера S´Q. Пример: В этом примере сначала с помощью функции premnmx выполняется масштабирование обучающей последовательности к диапазону [–1 1], затем создается и обучается нейронная сеть прямой передачи, выполняется ее моделирование и восстановление выхода с помощью функции postmnmx. P = [–0.92 0.73 –0.47 0.74 0.29; –0.08 0.86 –0.67 –0.52 0.93]; t = [–0.08 3.40 –0.82 0.69 3.10]; [pn,minp,maxp,tn,mint,maxt] = premnmx(P,t); net = newff(minmax(pn),[5 1],{'tansig' 'purelin'},'trainlm'); net = train(net,pn,tn); an = sim(net,pn) an = –0.6493 1.0000 –1.0000 –0.2844 0.8578 a = postmnmx(an,mint,maxt) a = –0.0800 3.4000 –0.8200 0.6900 3.1000 Восстановленный вектор выхода нейронной сети совпадает с исходным вектором целей. Алгоритм: Восстановление данных, масштабированных к диапазону [–1 1], выполняется по формуле p = 0.5*(pn + 1)*(maxp – minp) + minp. Сопутствующие функции: PREMNMX, PREPCA, POSTSTD.
Синтаксис: [p,t] = poststd(pn,meanp,stdp,tn,meant,stdt) p = poststd(pn,meanp,stdp) Описание: Функция poststd выполняет постпроцессорную обработку, связанную с восстановлением данных, которые были масштабированы к нормальному закону распределения Входные аргументы: pn – матрица масштабированных векторов входа размера R´Q; meanp – вектор средних значений исходного массива входов размера R´1; stdp – вектор среднеквадратичных отклонений исходного массива входов размера R´1; tn – матрица масштабированных векторов целей размера S´Q; meant – вектор средних значений массива целей размера S´1; stdt – вектор среднеквадратичных отклонений массива целей размера S´1. Выходные аргументы: p – восстановленная матрица векторов входа размера R´Q; t – восстановленная матрица векторов целей размера S´Q. Примеры: В этом примере сначала с помощью функции prestd выполняется масштабирование обучающей последовательности к нормальному закону распределения с параметрами p = [–0.92 0.73 –0.47 0.74 0.29; –0.08 0.86 –0.67 –0.52 0.93]; t = [–0.08 3.40 –0.82 0.69 3.10]; [pn,meanp,stdp,tn,meant,stdt] = prestd(p,t); net = newff(minmax(pn),[5 1],{'tansig' 'purelin'},'trainlm'); net = train(net,pn,tn); an = sim(net,pn) an = –0.7049 1.1285 –1.0947 –0.2992 0.9704 a = poststd(an,meant,stdt) a = –0.0800 3.4000 –0.8200 0.6900 3.1000 Восстановленный вектор выхода нейронной сети совпадает с исходным вектором целей. Алгоритм: Восстановление данных, масштабированных к нормальному закону распределения p = stdp * pn + meanp. Сопутствующие функции: PREMNMX, PREPCA, POSTMNMX, PRESTD.
Синтаксис: [m,b,r] = postreg(A,T) Описание: Функция [m, b, r] = postreg(A, T) выполняет постпроцессорную обработку выхода нейронной сети и рассчитывает линейную регрессию между векторами выхода и цели. Входные аргументы: A – 1´Q массив выходов сети, каждый элемент которого выход сети; T – 1´Q массив целей, каждый элемент которого целевой вектор. Выходные аргументы: m – наклон линии регрессии; b – точка пересечения линии регрессии с осью Y; r – коэффициент регрессии. Примеры: В данном примере с помощью функции prestd нормализуется множество обучающих данных, на нормализованных данных вычисляются главные компоненты, создается и обучается сеть, затем сеть моделируется. Выход сети с помощью функции poststd денормализуется и вычисляется линейная регрессия между выходом (ненормализованным) сети P = [–0.92 0.73 –0.47 0.74 0.29; –0.08 0.86 –0.67 –0.52 0.93]; T = [–0.08 3.40 –0.82 0.69 3.10]; [pn,meanp,stdp,tn,meant,stdt] = prestd(P,T); [ptrans,transMat] = prepca(pn,0.02); net = newff(minmax(ptrans),[5 1],{'tansig' 'purelin'},'trainlm'); net = train(net,ptrans,tn); an = sim(net,ptrans) an = –0.7049 1.1285 –1.0947 –0.2992 0.9704 a = poststd(an,meant,stdt) a = –0.0800 3.4000 –0.8200 0.6900 3.1000 [m,b,r] = postreg(a,t) % Рис.11.61 m = 1.0000 b = 5.6881e–014 r = 1.0000 В данном примере параметры линейной регрессии свидетельствуют о хорошей согласованности векторов выхода нейронной сети и цели, и это означает, что синтезированная нейронная сеть успешно реализует свою функцию.
Сопутствующие функции: PREMNMX, PREPCA.
Синтаксис: pn = tramnmx(p,minp,maxp) Описание: Функция pn = tramnmx(p, minp, maxp) приводит текущие входные данные к диапазону Входные аргументы: p – матрица векторов входа размера R´Q; minp – вектор минимальных элементов входа размера R´1; maxp – вектор максимальных элементов входа размера R´1. Выходные аргументы: pn – матрица нормированных векторов входа размера R´Q. Пример: Следующие операторы масштабируют обучающую последовательность к диапазону [–1 1], формируют и обучают нейронную сеть прямой передачи. p = [–10 –7.5 –5 –2.5 0 2.5 5 7.5 10]; t = [0 7.07 –10 –7.07 0 7.07 10 7.07 0]; [pn,minp,maxp,tn,mint,maxt] = premnmx(p,t); net = newff(minmax(pn),[5 1],{‘tansig’ ‘purelin’},’trainlm’); net = train(net,pn,tn); Если в дальнейшем к обученной сети будут приложены новые входы, то они должны быть масштабированы с помощью функции tramnmx. Выход сети должен быть восстановлен с помощью функции postmnmx. p2 = [4 –7]; pn = tramnmx(p2,minp,maxp); an = sim(net,pn) an = 0.9552 0.8589 a = postmnmx(an,mint,maxt) a = 9.5518 8.5893 Алгоритм: Масштабирование текущих данных к диапазону [–1 1] выполняется по формуле pn = 2 * (p – minp)/(maxp – minp) – 1. Сопутствующие функции: PREMNMX, PRESTD, PREPCA, TRASTD, TRAPCA.
Синтаксис: pn = trastd(p,meanp,stdp) Описание: Функция pn = trastd(p, meanp, stdp) приводит текущие входные данные к нормальному закону распределения с параметрами [0 1], если они принадлежат к множеству с известными средним значением и среднеквадратичным отклонением. Эта функция применяется, когда нейронная сеть была обучена с помощью данных, нормированных функцией prestd. Входные аргументы: p – матрица векторов входа размера R´Q; meanp – вектор средних значений элементов входа размера R´1; stdp – вектор среднеквадратичных отклонений элементов входа размера R´1. Выходные аргументы: pn – матрица нормированных векторов входа размера R´Q. Пример: Следующие операторы масштабируют обучающую последовательность к нормальному закону распределения с параметрами [0 1], формируют и обучают нейронную сеть прямой передачи. p = [–0.92 0.73 –0.47 0.74 0.29; –0.08 0.86 –0.67 –0.52 0.93]; t = [–0.08 3.4 –0.82 0.69 3.1]; [pn,meanp,stdp,tn,meant,stdt] = prestd(p,t); net = newff(minmax(pn),[5 1],{'tansig' 'purelin'},'trainlm'); net = train(net,pn,tn); Если в дальнейшем к обученной сети будут приложены новые входы, то они должны быть масштабированы с помощью функции trastd. Выход сети должен быть восстановлен с помощью функции poststd. p2 = [1.5 –0.8; 0.05 –0.3]; pn = trastd(p2,meanp,stdp); an = sim(net,pn) an = 0.8262 –1.0585 a = poststd(an,meant,stdt) a = 2.8262 –0.7512 Алгоритм: Масштабирование текущих данных к нормальному закону распределения с параметрами [0 1] выполняется по формуле pn = (p – meanp)/stdp. Сопутствующие функции: PREMNMX, PREPCA, PRESTD, TRAPCA, TRAMNMX.
Синтаксис: Ptrans = trapca(P,TransMat) Описание: Функция Ptrans = trapca(P, TransMat) преобразует текущие входные данные с учетом факторного анализа, примененного к обучающей последовательности. Эта функция применяется, когда нейронная сеть была обучена с помощью данных, предварительно обработанных функциями prestd и prepca. Входные аргументы: P – матрица текущих векторов входа размера R´Q; TransMat – матрица преобразования, связанная с факторным анализом. Выходные аргументы: Ptrans – преобразованный массив векторов входа. Пример: Следующие операторы выполняют главный факторный анализ обучающей последовательности, удерживая только те компоненты, которые имеют дисперсию, превышающую значение 0.02. P = [–1.5 –0.58 0.21 –0.96 –0.79; –2.2 –0.87 0.31 –1.40 –1.20]; t = [–0.08 3.4 –0.82 0.69 3.1]; [pn,meanp,stdp,tn,meant,stdt] = prestd(P,t); [ptrans,transMat] = prepca(pn,0.02) ptrans = 1.7519 –0.3194 –2.1274 0.5212 0.1738 transMat = –0.7071 –0.7071 net = newff(minmax(ptrans),[5 1],{'tansig' 'purelin'},'trainlm'); net = train(net,ptrans,tn); Если в дальнейшем к сети будут приложены новые входы, то они должны быть масштабированы с помощью функций trastd и trapca. Выход сети должен быть восстановлен p2 = [1.50 –0.8; 0.05 –0.3]; p2n = trastd(p2,meanp,stdp); p2trans = trapca(p2n,transMat) p2trans = –3.3893 –0.5106 an = sim(net,p2trans) an = 0.7192 1.1292 a = poststd(an,meant,stdt) a = 2.6231 3.4013 Алгоритм: Масштабирование текущих данных с учетом факторного анализа выполняется Ptrans = TransMat * P. Сопутствующие функции: PRESTD, PREMNMX, PREPCA, TRASTD, TRAMNMX. Вспомогательные функции Ниже представлены различные утилиты, которые составляют ядро ППП Neural Network Toolbox. В первую очередь это утилиты для вычисления сигналов в различных точках нейронной сети, а также функционала качества обучения сети и связанных с ним вычислений градиента, а также функций Якоби и Гессе. Значительное место занимают реализации операций с массивами и матрицами, а также утилиты графики, позволяющие отображать входные данные, топологию сетей, строить поверхности ошибок и тректории обучения в пространстве параметров нейронной сети. Утилиты вычислений
Синтаксис: [Ac,N,LWZ,IWZ,BZ] = calca(net,Pd,Ai,Q,TS) Описание: Функция [Ac, N, LWZ, IWZ, BZ] = calca(net, Pd, Ai, Q, TS) вычисляет сигналы в слоях нейронной сети как реакцию на входы c учетом линий задержки. Входные аргументы: net – имя нейронной сети; Pd – выходы линий задержки; Ai – начальные условия на линиях задержки по выходам слоев; Q – количество выборок для фиксированного момента времени; TS – число шагов по времени. Выходные аргументы: Ac – массив векторов, объединяющих выходы нейронов и слоя; N – входы функций активации; LWZ – массив взвешенных выходов слоя; IWZ – массив взвешенных входов; BZ – массив смещений. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, тремя нейронами и линией задержки на входе с параметрами [0 2 4]; в сети используется обратная связь с линией задержки [1 2] (рис. 11.62). net = newlin([0 1],3,[0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2];
Рис. 11.62 Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для восьми шагов по времени, вектор начальных условий на линии задержки входов Pi: P = {0 0.1 0.3 0.6 0.4 0.7 0.2 0.1}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,8,1,Pc) Pd(:,:,1) = [3´1 double] Pd(:,:,2) = [3´1 double] ... Pd(:,:,8) = [3´1 double] Сформируем вектор начальных условий на линии задержки выхода слоя для каждого Ai = {[0.5; 0.1; 0.2] [0.6; 0.5; 0.2]}; Применяя функцию calca, рассчитаем сигналы в слое на каждом временном шаге TS: [Ac,N,LWZ,IWZ,BZ] = calca(net,Pd,Ai,1,8) Ac = Columns 1 through 4 [3´1 double] [3´1 double] [3´1 double] [3´1 double] [3´1 double] [3´1 double] [3´1 double] [3´1 double]
Columns 9 through 10 [3´1 double] [3´1 double] N = Columns 1 through 4 [3´1 double] [3´1 double] [3´1 double] [3´1 double] Columns 5 through 8 [3´1 double] [3´1 double] [3´1 double] [3´1 double] LWZ(:,:,1) = [3´1 double] LWZ(:,:,2) = [3´1 double] ... LWZ(:,:,8) = [3´1 double] IWZ(:,:,1) = [3´1 double] IWZ(:,:,2) = [3´1 double] ... IWZ(:,:,8) = [3´1 double] BZ = [3´1 double] Сопутствующие функции: CALCA1, CALCPD.
Синтаксис: [Ac,N,LWZ,IWZ,BZ] = calca1(net,Pd,Ai,Q) Описание: Функция [Ac, N, LWZ, IWZ, BZ] = calca1(net, Pd, Ai, Q) вычисляет сигналы в слоях нейронной сети как реакцию на входы c учетом линий задержки для одного шага по времени. Эта функция применяется в последовательных процедурах обучения с использованием функции trains, которые требуют вычисления реакции сети на каждом шаге по времени. Входные аргументы: net – имя нейронной сети; Pd – выходы линий задержки; Ai – начальные условия на линиях задержки по выходам слоев; Q – количество реализаций для фиксированного момента времени. Выходные аргументы: Ac – массив векторов, объединяющих выходы нейронов и слоя; N – входы функций активации; LWZ – массив взвешенных выходов слоя; IWZ – массив взвешенных входов; BZ – массив смещений. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, тремя нейронами и линией задержки на входе с параметрами [0 2 4]; в сети используется обратная связь с ЛЗ [1 2] (см. рис. 11.62). net = newlin([0 1],3,[0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2]; Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для трех шагов по времени, вектор начальных условий на линии задержки входов Pi: P = {0 0.1 0.3}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,3,1,Pc) Pd(:,:,1) = [3´1 double] Pd(:,:,2) = [3´1 double] Pd(:,:,3) = [3´1 double] Сформируем вектор начальных условий на линии задержки выхода слоя для каждого Ai = {[0.5; 0.1; 0.2] [0.6; 0.5; 0.2]}; Применяя функцию calca1, рассчитаем сигналы в слое на первом шаге по времени: [A1,N1,LWZ1,IWZ1,BZ1] = calca1(net,Pd(:,:,1),Ai,1) A1 = [3´1 double] N1 = [3´1 double] LWZ1 = [3´1 double] IWZ1 = [3´1 double] BZ1 = [3´1 double] Теперь можно вычислить новые состояния на ЛЗ, используя массивы Ai и A, и рассчитать сигналы слоя на втором шаге по времени: Ai2 = [Ai(:,2:end) A1]; [A2,N2,LWZ2,IWZ2,BZ2] = calca1(net,Pd(:,:,2),Ai2,1) A2 = [3´1 double] N2 = [3´1 double] LWZ2 = [3´1 double] IWZ2 = [3´1 double] BZ2 = [3´1 double] Сопутствующие функции: CALCA, CALCPD.
Синтаксис: Pd = calcpd(net,TS,Q,Pc) Описание: Функция Pd = calcpd(net, TS, Q, Pc) вычисляет запаздывающие входы сети после их прохождения через ЛЗ. Входные аргументы: net – имя нейронной сети; TS – число элементов во временной выборке; Q – число выборок; Pc – массив векторов, объединяющий векторы входов сети и начальных условий на ЛЗ. Выходные аргументы: Pd – массив запаздывающих входов. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, тремя нейронами и линией задержки на входе с параметрами [0 2 4]: net = newlin([0 1],3,[0 2 4]); Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для трех шагов по времени и вектор начальных условий на линии задержки Pi: P = {0 0.1 0.3}; Pi = {0.2 0.3 0.4 0.1}; Запаздывающие входы (значения входов после прохождения через ЛЗ) рассчитываются с помощью функции calcpd после их объединения в вектор Рс: Pc = [Pi P]; Pd = calcpd(net,3,1,Pc) Pd(:,:,1) = [3´1 double] Pd(:,:,2) = [3´1 double] Pd(:,:,3) = [3´1 double] Теперь можно просмотреть значения запаздывающих входов для двух первых шагов: Pd{1,1,1} ans = 0.4000 0.2000 Pd{1,1,2} ans = 0.1000 0.1000 0.3000 Сопутствующие функции: CALCA, CALCA1.
Синтаксис: El = calce(net,Ac,Tl,TS) Описание: Функция El = calce(net, Ac, Tl, TS) рассчитывает ошибки слоя нейронной сети на интервале времени TS. Входные аргументы: net – имя нейронной сети; Tl – массив векторов целей слоя; Ac – массив векторов, объединяющих выходы нейронов и слоя; Q – количество выборок для фиксированного момента времени. Выходные аргументы: El – массив ошибок слоя на интервале времени TS. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, net = newlin([0 1],2,[0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2]; Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для пяти шагов по времени, вектор начальных условий на ЛЗ входов Pi: P = {0 0.1 0.3 0.6 0.4}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,5,1,Pc); Сформируем вектор начальных условий на ЛЗ выхода слоя для каждого из двух нейронов и рассчитаем сигналы в слое на пяти шагах по времени: Ai = {[0.5; 0.1] [0.6; 0.5]}; [Ac,N,LWZ,IWZ,BZ] = calca(net,Pd,Ai,1,5); Определим цели слоя для двух нейронов для каждого из пяти временных шагов Tl = {[0.1;0.2] [0.3;0.1], [0.5;0.6] [0.8;0.9], [0.5;0.1]}; El = calce(net,Ac,Tl,5) El = [2´1 double] [2´1 double] [2´1 double] [2´1 double] [2´1 double] Просмотрим ошибки слоя 1 на временном шаге 2: El{1,2} ans = 0.3000 0.1000 Сопутствующие функции: CALCA, CALCE1, CALCPD.
Синтаксис: El = calce1(net,A,Tl) Описание: Функция El = calce(net, Ac, Tl) рассчитывает ошибки слоя нейронной сети на одном шаге по времени. Входные аргументы: net – имя нейронной сети; A – массив выходов слоя на одном шаге; Tl – массив векторов целей слоя. Выходные аргументы: El – массив ошибок слоя на одном шаге по времени. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, net = newlin([0 1],2,[0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2]; Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для пяти шагов по времени, вектор начальных условий на ЛЗ входов Pi: P = {0 0.1 0.3 0.6 0.4}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,5,1,Pc); Сформируем вектор начальных условий на ЛЗ выхода слоя для каждого из двух нейронов и рассчитаем сигналы в слое на пяти шагах по времени: Ai = {[0.5; 0.1] [0.6; 0.5]}; [A1,N1,LWZ1,IWZ1,BZ1] = calca1(net,Pd(:,:,1),Ai,1) Определим цели слоя для двух нейронов для каждого из пяти временных шагов и рассчитаем ошибки слоя на первом шаге: Tl = {[0.1;0.2] [0.3;0.1], [0.5;0.6] [0.8;0.9], [0.5;0.1]}; El = calce1(net,A1,Tl(:,1)) El = [2´1 double] Просмотрим ошибку слоя на первом шаге: El{1} ans = 0.1000 0.2000 Теперь можно вычислить новые состояния на ЛЗ, используя массивы Ai и A, и рассчитать сигналы слоя на втором шаге по времени: Ai2 = [Ai(:,2:end) A1]; [A2,N2,LWZ2,IWZ2,BZ2] = calca1(net,Pd(:,:,2),Ai2,1); El = calce1(net,A2,Tl(:,2)) El{1} ans = 0.3000 0.1000 Сопутствующие функции: CALCA1, CALCE, CALCPD.
Синтаксис: X = formx(net,B,IW,LW) Описание: Функция X = formx(net, B, IW, LW) извлекает из описания сети матрицы весов и векторы смещений и объединяет их в единый вектор. Входные аргументы: net – нейронная сеть; B – массив ячеек размера Nl´1, включающий векторы смещений для Nl слоев; IW – массив ячеек размера Nl´1, включающий матрицы весов входа; LW – массив ячеек размера Nl´Nl, состоящий из весовых матриц Nl слоев. Выходные аргументы: X – объединенный вектор весов и смещений. Примеры: Создадим однослойную сеть с тремя нейронами и двухэлементным вектором входа net = newff([0 1; –1 1],[3]); Выведем значения массивов весов и смещений: b = net.b b = [3´1 double] b{1} ans = 3.7981 –0.9154 –1.6816 iw = net.iw iw = [3´2 double] iw{1} ans = –2.7464 1.9986 1.8307 2.2455 –1.4865 –2.3082 lw = net.lw lw = {[]} Объединим массивы весов и смещений в общий вектор: x = formx(net,net.b,net.iw,net.lw); x' ans = –2.7464 1.8307 –1.4865 1.9986 2.2455 –2.3082 3.7981 –0.9154 –1.6816 В результате сформирован единый вектор, в котором сначала расположены элементы весовой матрицы по столбцам, а затем присоединен вектор смещений. Сопутствующие функции: GETX, SETX.
Синтаксис: X = getx(net) Описание: Функция X = getx(net) извлекает объединенный вектор весов и смещений, если известен дескриптор нейронной сети net. Пример: Создадим однослойную сеть с тремя нейронами и двухэлементным вектором входа net = newff([0 1; –1 1],[3]); Выведем значения массивов весов и смещений: net.iw{1,1} ans = –4.7161 0.5653 3.5899 1.6304 –0.6304 2.4043 net.b{1} ans = 4.7829 –1.7950 –2.1097 Эти же значения можно вывести в виде объединенного вектора, который содержится в описании нейронной сети: x = getx(net); x' ans = –4.7161 3.5899 –0.6304 0.5653 1.6304 2.4043 4.7829 –1.7950 –2.1097 Сопутствующие функции: SETX, FORMX.
Синтаксис: net = setx(net,X) Описание: Функция net = setx(net, X) включает объединенный вектор весов и смещений X в описание нейронной сети с дескриптором net. Пример: Создадим однослойную сеть с тремя нейронами и двухэлементным вектором входа net = newff([0 1; –1 1],[3]); net.iw net.b ans = [3´2 double] ans = [3´1 double] Сеть имеет 6 весовых коэффициентов и 3 элемента смещений, т. е. всего 9 значений. net = setx(net,rand(9,1)); Эти значения можно вывести на экран с помощью команды getx(net). Сопутствующие функции: GETX, FORMX.
Синтаксис: [perf,El,Ac,N,BZ,IWZ,LWZ] = calcperf(net,X,Pd,Tl,Ai,Q,TS) Описание: Функция [perf, El, Ac, N, LWZ, IWZ, BZ] = calcperf(net, X, Pd, Tl, Ai, Q, TS) вычисляет функционал качества и сигналы в слое нейронной сети net. Входные аргументы: net – имя нейронной сети; X – объединенный вектор весов и смещений; Pd – массив задержанных входов; Tl – массив векторов целей слоя; Ai – начальные условия на линиях задержки в слоях; Q – число выборок; TS – размер выборки. Выходные аргументы: perf – значение функционала качества; El – массив ошибок слоя; Ac – массив векторов, объединяющих выходы нейронов и слоя; N – входы функций активации; LWZ – массив взвешенных выходов слоя; IWZ – массив взвешенных входов; BZ – массив смещений. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, двумя нейронами и ЛЗ на входе с параметрами [0 2 4]; в сети используется обратная связь net = newlin([0 1],2,[0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2]; Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для пяти шагов по времени, вектор начальных условий на ЛЗ входов Pi: P = {0 0.1 0.3 0.6 0.4}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,5,1,Pc); Сформируем вектор начальных условий на ЛЗ выхода слоя для каждого из двух нейронов и массив векторов целей на пяти шагах по времени: Ai = {[0.5; 0.1] [0.6; 0.5]}; Tl = {[0.1;0.2] [0.3;0.1], [0.5;0.6] [0.8;0.9], [0.5;0.1]}; Извлечем объединенный вектор весов и смещений из описания сети X = getx(net); Вычислим функционал качества и сигналы в сети [perf,El,Ac,N,BZ,IWZ,LWZ] = calcperf(net,X,Pd,Tl,Ai,1,5); Выведем значения функционала качества и массива ошибок слоя perf perf = 0.2470 cat(2, El{:}) ans = 0.1000 0.3000 0.5000 0.8000 0.5000 0.2000 0.1000 0.6000 0.9000 0.1000 Сопутствующие функции: CALCGX, CALCPD, GETX.
Синтаксис: [gX,normgX] = calcgx(net,X,Pd,BZ,IWZ,LWZ,N,Ac,El,perf,Q,TS) Описание: Функция [gX, normgX] = calcgx(net, X, Pd, BZ, IWZ, LWZ, N, Ac, El, perf, Q, TS) вычисляет градиент функционала качества по объединенному вектору весов и смещений X. Если слой не имеет ЛЗ, то результатом является истинный градиент; если сеть имеет ЛЗ, то результатом является аппроксимация градиента, называемая градиентом Элмана. Входные аргументы: net – имя нейронной сети; X – объединенный вектор весов и смещений; Pd – массив задержанных входов; BZ – массив векторов смещений; IWZ – массив взвешенных входов слоя; LWZ – массив взвешенных выходов слоя; N – массив входов функций активации; Ac – массив векторов, объединяющих выходы нейронов и слоя; El – массив ошибок слоя; perf – значение функционала качества; Q – число выборок; TS – размер выборки. Выходные аргументы: gX – градиент dPerf/dX; normgX – значение нормы градиента. Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, net = newlin([0 1],2,[0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2]; Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для пяти шагов по времени, вектор начальных условий на ЛЗ входов Pi: P = {0 0.1 0.3 0.6 0.4}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,5,1,Pc); Сформируем вектор начальных условий на ЛЗ выхода слоя для каждого из двух нейронов и массив векторов целей на пяти шагах по времени: Ai = {[0.5; 0.1] [0.6; 0.5]}; Tl = {[0.1;0.2] [0.3;0.1], [0.5;0.6] [0.8;0.9], [0.5;0.1]}; Извлечем из описания сети объединенный вектор весов и смещений сети и вычислим функционал качества и сигналы сети: X = getx(net); [perf,El,Ac,N,BZ,IWZ,LWZ] = calcperf(net,X,Pd,Tl,Ai,1,5); В заключение используем функцию calcgx, чтобы вычислить градиент функционала по объединенному вектору весов и смещений: [gX,normgX] = calcgx(net,X,Pd,BZ,IWZ,LWZ,N,Ac,El,perf,1,5); gX' ans = 0.172 0.154 0.06 0.042 0.078 0.08 0.012 0.024 0.01 0.020 0.046 0.032 0.032 0.014 0.44 0.380 normgX normgX = 0.6440 Поскольку в сети присутствуют ЛЗ, то в данном случае вычисляется градиент Элмана. Сопутствующие функции: CALCJX, CALCJEJJ.
Синтаксис: jx = calcjx(net,PD,BZ,IWZ,LWZ,N,Ac,Q,TS) Описание: Функция jX = calcjx(net, PD, BZ, IWZ, LWZ, N, Ac, Q, TS) вычисляет функцию Якоби функционала качества относительно объединенной матрицы весов и смещений. Входные аргументы: net – имя нейронной сети; PD – массив задержанных входов; BZ – массив векторов смещений; IWZ – массив взвешенных векторов входа; LWZ – массив взвешенных векторов выхода; N – массив входов функций активации; Ac – массив векторов, объединяющих выходы нейронов и слоя; Q – число выборок; TS – размер выборки. Выходные аргументы: jX – якобиан функционала качества относительно объединенной матрицы весов Пример: Создадим линейную сеть с одним входом, изменяющимся в диапазоне от 0 до 1, net = newlin([0 1],2, [0 2 4]); net.layerConnect(1,1) = 1; net.layerWeights{1,1}.delays = [1 2]; Вычислим вектор запаздывающих входов Pd, если заданы реализация вектора входа P для пяти шагов по времени, вектор начальных условий на ЛЗ входов Pi: P = {0 0.1 0.3 0.6 0.4}; Pi = {0.2 0.3 0.4 0.1}; Pc = [Pi P]; Pd = calcpd(net,5,1,Pc); Зададим 2 начальных значения запаздывающих выходов слоя для каждого из двух нейронов и цели слоя для двух нейронов на 5 шагов по времени: Ai = {[0.5; 0.1] [0.6; 0.5]}; Tl = {[0.1;0.2] [0.3;0.1], [0.5;0.6] [0.8;0.9], [0.5;0.1]}; Извлечем из описания сети объединенный вектор весов и смещений сети и вычислим функционал качества и сигналы сети: X = getx(net); [perf,El,Ac,N,BZ,IWZ,LWZ] = calcperf(net,X,Pd,Tl,Ai,1,5); Теперь можно применить функцию calcjx, чтобы вычислить якобиан функционала jX = calcjx(net,Pd,BZ,IWZ,LWZ,N,Ac,1,5); jX jX =
Сопутствующие функции: CALCGX, CALCJEJJ.
Синтаксис: [je,jj,normje] = calcjejj(net,Pd,BZ,IWZ,LWZ,N,Ac,El,Q,TS,MR) Описание: Функция [je, jj, normgX] = calcjejj(net, PD, BZ, IWZ, LWZ, N, Ac, El, Q, TS, MR) вычисляет градиент, матрицу, аппроксимирующую гессиан, и норму градиента функционала качества. Входные аргументы: net – имя нейронной сети; PD – массив задержанных входов; BZ – массив векторов смещений; IWZ – массив взвешенных векторов входа; LWZ – массив взвешенных векторов выхода; N – массив входов функций активации; Ac – массив векторов, объединяющих выходы нейронов и слоя; El – массив ошибок слоя; Q – число выборок; TS – размер выборки; MR – коэффициент экономии памяти. Выходные аргументы: je – градиент функционала качества; jj – матрица, аппроксимирующая гессиан функционала качества; normgX – норма градиента функционала качества. Применение функции: Функция calcjejj вычисляет градиент je и матрицу jj, аппроксимирующую гессиан функционала качества, которые используются в алгоритмах минимизации функции многих переменных. Функционал качества как функция настраиваемых параметров нейронной сети и является такой многомерной функцией. Как градиент, так и матрица, аппроксимирующая гессиан функционала качества, градиент рассчитывается по формуле

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
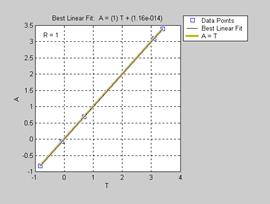 Рис. 11.61
Рис. 11.61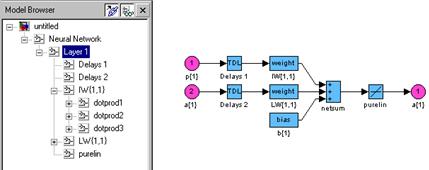
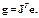 (11.10)
(11.10)