
|
|
Закон распределения вероятностей дискретной случайной величины. Законы биномиальный и ПуассонаДискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т. е. между двумя соседними возможными значениями нет возможных значений), которые эта величина принимает с определенными вероятностями. Другими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (в последнем случае множество всех возможных значений называют счетным). Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть задан в виде таблицы, первая строка которой содержит возможные значения xį, а вторая — вероятности рį: X
где Если множество возможных значений X бесконечно (счетно), то ряд Закон распределения дискретной случайной величины X может быть также задан аналитически (в виде формулы)
или с помощью функции распределения (см. гл. VI, § 1). Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят Биномиальнымназывают закон распределения дискретной случайной величины Х-—числа появлений события в п независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения Х = k (числа k появлении события) вычисляют по формуле Бернулли:
Если число испытаний велико, а вероятность р появления события в каждом испытании очень мала, то используют приближенную бытия формулу
где k – число появлений события в п независимых испытаниях, λ = пр (среднее число появлений события в п испытаниях), и говорят, что случайная величина распределена по закону Пуассона. 54. Дискретная случайная величина X задана законом распределения: X 1 3 6 8 р 0,2 0,1 0,4 0,3 Построить многоугольник распределения. Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xį, а по оси ординат — соответствующие вероятности рį -. Построим точки
55. Дискретная случайная величина X задана законом распределения: а) X 2 4 5 6 б) X 10 15 20 р 0,3 0,1 0,2 0,4 р 0,1 0,7 0,2 Построить многоугольник распределения. 56. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Решение. Дискретная случайная величина X (число отказавших элементов в одном опыте) имеет следующие возможные значения: х1 = 0 (ни один из элементов устройства не отказал), x2 = 1 (отказал один элемент), х3 = 2 (отказали два элемента) и х4 = 3 (отказали три элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, п = 3, р = 0,1 (следовательно, q= 1 – 0,1=0,9), получим:
Контроль: 0,729 + 0,243 + 0,027 + 0,001 =1. Напишем искомый биномиальный закон распределения X: X 0 1 2 3 р 0,729 0,243 0,027 0,001 57.В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X — числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения. 58.Написать биномиальный закон распределения дискретной случайной величины X — числа появлений «герба» при двух бросаниях монеты. 59.Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X—числа выпадений четного числа очков на двух игральных костях. 60.В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных *). Решение. Случайная величина X — число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х1 = 0 ; x2 = 1; х3 = 2. Найдем вероятности возможных значений X по формуле (см. задачу 17, гл. 1, § 1)
(N – число деталей в партии, п –число стандартных деталей в партии, т – число отобранных деталей, k – число стандартных деталей среди отобранных находим;
Составим искомый закон распределения: X 0 1 2 р 1/45 16/45 28/45 Контроль: 1/45+16/45 + 28/45=1. 61.В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных. 62.После ответа студента на вопросы экзаменационного билета экзаменатор задает студенту дополнительные вопросы. Преподаватель прекращает задавать дополнительные вопросы, как только студент обнаруживает незнание заданного вопроса. Вероятность того, что студент ответит на любой заданный дополнительный вопрос, равна 0,9. Требуется: а) составить закон распределения случайной дискретной величины X — числа дополнительных вопросов, которые задаст преподаватель студенту; б) найти наивероятнейшее число k0 заданных студенту дополнительных вопросов. Решение, а) Дискретная случайная величина X — число заданных дополнительных вопросов—имеет следующие возможные значения: x1=l, х2=2, х3=3, ,.., Xn = k, ... Найдем вероятности этих возможных значений. Величина X примет возможное значение x=l (экзаменатор задаст только один вопрос), если студент не ответит на первый вопрос. Вероятность этого возможного значения равна 1—0,9 = 0,1. Таким образом, Р(Х=1) = 0,1. Величина X примет возможное значение х2 = 2 (экзаменатор задаст только два вопроса), если студент ответит на первый вопрос (вероятность этого события равна 0,9) и не ответит на второй (вероятность этого события равна 0,1). Таким образом, Р (Х=2)=0,9-0,1 =0,09. Аналогично найдем
Напишем искомый закон распределения: X 1 2 3 … k ... р 0,1 0,09 0,081 ... б) Наивероятнейшее число k0 заданных вопросов (наивероятнейшее значение Х,) т.е число заданных преподавателем вопросов, которое имеет наибольшую вероятность, как следует из закона распределения, равно единице. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
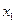
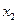 ….
…. 


 ….
…. 
 .
.
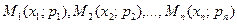 (xį,—возможные значения X,
(xį,—возможные значения X, 


 и
и  . Соединив эти точки отрезками прямых, получим искомый многоугольник распределения (рис. 5).
. Соединив эти точки отрезками прямых, получим искомый многоугольник распределения (рис. 5). ;
; 
 ;
; 








 ...
...