
|
|
Геометрические вероятностиРаздел 7. Теория вероятностей
Классическое и статистическое определение вероятности При классическом определении вероятность события определяется равенством P(A)=m/n, где m – число элементарных исходов испытания, благоприятствующих появлению события А; n – общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны. Относительная частота события А определяется равенством W(A)=m/n, где т— число испытаний, в которых событие А наступило; n —общее число произведенных испытаний. При статистическом определении в качестве вероятности события принимают его относительную частоту. Примеры решения задач 1. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях — четная, причем на грани хотя бы одной из костей появится шестерка. Решение. На выпавшей грани «первой» игральной кости может появиться одно очко, два очка, ....,шесть очков. Аналогичные шесть элементарных исходов возможны при бросании «второй» кости. Каждый из исходов бросания «первой» кости может сочетаться с каждым из исходов бросания «второй». Таким образом, общее число возможных элементарных исходов испытания равно 6∙6=36. Эти исходы образуют полную группу и в силу симметрии костей равновозможны. Благоприятствующими интересующему нас событию (хотя бы на одной грани появится шестерка, сумма выпавших очков – четная) являются следующие пять исходов (первым записано число очков, выпавших на «первой» кости, вторым – число очков, выпавших на «второй» кости; далее найдена сумма очков): 1) 6, 2; 6+2 = 8, 2) 6, 4; 6+4=10. 3) 6, 6; 6+6=12, 4) 2. 6; 2+6=8, 5) 4. 6; 4+6=10. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов: Р=5/36. 2. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь. Решение, а) Извлеченная стандартная деталь, очевидно, не могла быть утеряна; могла быть потеряна любая из остальных 30 деталей (21+10–1=30), причем среди них было 20 стандартных (21–1=20). Вероятность того, что была потеряна стандартная деталь, Р=20/30=2/3. б) Среди 30 детален, каждая из которых могла быть утеряна, было 10 нестандартных. Вероятность того, что потеряна нестандартная деталь. Р=10/30=1/3. 3. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны. 4. Указать ошибку «решения» задачи: брошены две игральные кости; найти вероятность того, что сумма выпавших очков равна 3 (событие А). «Решение». Возможны два исхода испытания: сумма выпавших очков равна 3, сумма выпавших очков не равна 3. Событию А благоприятствует один исход; общее число исходов равно двум. Следовательно, искомая вероятность Р(А)=1/2. Ошибка этого «решения» состоит в том, что рассматриваемые исходы не являются равновозможными. Правильное решение. Общее число равновозможных исходов равно 6∙6=36 (каждое число очков, выпавших на одной кости, может сочетаться со всеми числами очков, выпавших на другой кости). Среди этих исходов благоприятствуют событию А только два исхода (в скобках указаны числа выпавших очков): (1; 2) и (2; 1). Следовательно, искомая вероятность Р(А)=2/36=1/18. 5. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность – четырем; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; г) сумма выпавших очков равна пяти, а произведение -- четырем. 6. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет окрашенных граней: а) одну; б) две; в) три. 7. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб». 8. В коробке шесть одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке. 9. Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (к не равные шести).
Решение. Общее число элементарных исходов испытания равно числу сочетаний из шести элементов по три, т. е. Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равного шести) на гранях двух других костей, равно числу сочетаний из пяти элементов по два, т. е. Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов: P= 10.В пачке 20 перфокарт, помеченных номерами 101, 102, ... , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120. 11. В ящике 10 одинаковых деталей, помеченных номерами 1, 2.....10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь № 1; б) детали № 1 и № 2. Решение. а) Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь шесть деталей из десяти, т. е. Найдем число исходов, благоприятствующих интересующему нас событию: среди отобранных шести деталей есть деталь № 1 и, следовательно, остальные пять деталей имеют другие номера. Число таких исходов, очевидно, равно числу способов, которыми можно отобрать пять деталей из оставшихся девяти, т.е. Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: P= б) Число исходов, благоприятствующих интересующему нас событию (среди отобранных деталей есть детали № 1 и № 2, следовательно, четыре детали имеют другие номера), равно числу способов, которыми можно извлечь четыре детали из оставшихся восьми, т. е. Искомая вероятность 12. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. 13. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная. 14. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных. 15. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы. 16. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры. 17. В партии из N деталей имеется п стандартных. Наудачу отобраны т деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных. Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь m деталей из N деталей, т. е. Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди т деталей ровно k стандартных): k стандартных деталей можно взять из п. стандартных деталей Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
18. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины. 19. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода. 20. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников. 21. В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие. 22. В «секретном» замке на общей оси четыре диска, каждый из которых разделен на пять секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт. 23. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг. Решение. Относительная частота события А (появление бракованных книг) равна отношению числа испытаний, в которых появилось событие А, к общему числу произведенных испытаний: W(А)=5/100=0,05. 24. По цели произведено 20 выстрелов, причем зарегистрировано 18 попаданий. Найти относительную частоту попаданий в цель. 25. При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было проверено 200 приборов. Геометрические вероятности
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством P=Длина l /Длина L. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется равенством P=Площадь g / Площадь G. Аналогично определяется вероятность попадания точки в пространственную фигуру υ, которая составляет часть фигуры V: P=Объем υ / Объем V. 26. На отрезке L длины 20 см помещен меньший отрезок / длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. 27. На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую, чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси. 28. В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения. 29. Плоскость разграфлена параллельными прямыми, находящимися друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса r < а. Найти вероятность того, что монета не пересечет ни одной из прямых. 30. На плоскость с нанесенной сеткой квадратов со стороной а наудачу брошена монета радиуса r < а/2. Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади фигуры и не зависит от ее расположения. 31. На плоскость, разграфленную параллельными прямыми, отстоящими друг от друга на расстоянии 6 см, наудачу брошен круг радиуса 1 см. Найти вероятность того, что круг не пересечет ни одной из прямых. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. 32. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
. .
. .
.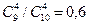 .
.
 .
. – числу сочетаний из N элементов по т.
– числу сочетаний из N элементов по т.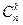 способами; при этом остальные т–k деталей должны быть нестандартными; взять же т–k нестандартных деталей из N–п нестандартных деталей можно
способами; при этом остальные т–k деталей должны быть нестандартными; взять же т–k нестандартных деталей из N–п нестандартных деталей можно  способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 
