
|
|
Цепь переменного синусоидального тока с последовательно соединенными катушкой и конденсаторомВключим к идеальному источнику синусоидальной э.д.с. последовательно
Г – генератор синусоидальной э.д.с.; рА – амперметр; К – катушка; С – конденсатор.
Составим расчётную схему Зададимся током в цепи
и найдём, каким должно быть в этом случае напряжение на зажимах
Подставим значение тока и получим:
Построим векторную диаграмму тока и напряжений этой цепи (рис.3.32).
Рассмотрим треугольник напряжений на векторной диаграмме (рис.3.33).
Введём понятие активной составляющей напряжения
и реактивной составляющей напряжения
Активная составляющая напряжения
Реактивная составляющая напряжения
где х – реактивное сопротивление цепи, Ом.
Разделим стороны треугольника напряжений на Im и получим треугольник
Полное сопротивление цепи
Запишем закон Ома для максимальных значений напряжения и тока:
для действующих значений напряжения и тока:
Умножим стороны треугольника сопротивлений на квадрат действующего
Коэффициент мощности цепи
Угол сдвига фаз цепи
Пример 3.11 К цепи, состоящей из последовательно соединённых катушки и конденсатора, Активное сопротивление цепи равно 6 Ом. Индуктивное сопротивление цепи равно 20 Ом. Ёмкостное сопротивление цепи равно 12 Ом. Выполнить анализ цепи. Решение. 1. Определяем полное сопротивление цепи по (3.110): 2. Определяем амплитуду тока по (3.111):
3. Определяем угол сдвига фаз цепи по (3.117):
4. Определяем реактивное сопротивление цепи, используя (3.108), и его характер: х = 20 – 12 = 8 Ом. Реактивное сопротивление цепи носит индуктивный характер, так как 20 > 12. 5. Определяем начальную фазу тока: yi = yu – j = 80 – 53 = 27°. 6. Записываем мгновенный ток: i = 28,2 sin (wt +27°) А. 7. Определяем амплитуду активной составляющей напряжения по (3.106): Uаm = Urm = 6×28,2 = 169,2 В. 8. Определяем начальную фазу активной составляющей напряжения: yur = yi= 27°. 9. Записываем мгновенное напряжение на активном сопротивлении: ur = 169,2 sin (wt +27°) В. 10. Определяем амплитуду напряжения на индуктивном сопротивлении по (3.73): ULm = 20×28,2 = 564 В. 11. Определяем начальную фазу напряжения на индуктивном сопротивлении: yuL = yi+ 90 = 27 + 90 = 117°. 12. Записываем мгновенное напряжение на индуктивном сопротивлении: uL = 564 sin (wt + 117°) В. 13. Определяем амплитуду напряжения на емкостном сопротивлении по (3.90): Uсm = 12×28,2 = 338,4 В. 14. Определяем начальную фазу напряжения на емкостном сопротивлении: yuс = yi– 90 = 27 – 90 = –63°. 15. Записываем мгновенное напряжение на емкостном сопротивлении: uс = 338,4 sin (wt – 63°) В. 16. Определяем амплитуду реактивной составляющей напряжения по (3.107): Uрm = 564 – 338,4 = 225,6 В. 17. Определяем действующее значение тока по (3.14):
18. Определяем активную мощность, потребляемую цепью, по (3.113): Р = 6×202 = 2400 Вт = 2,4 кВт. 19. Определяем реактивную мощность, потребляемую цепью, по (3.114): Q = 8×202 = 3200 вар = 3,2 квар. 20. Определяем полную мощность, потребляемую цепью, по (3.115): S = 10×202 = 4000 ва = 4,0 ква. 21. Определяем коэффициент мощности цепи по (3.116):
Вопросы для самоконтроля 1. Опишите физические явления, наблюдаемые в цепи переменного синусоидального 2. Составьте расчётную схему цепи с идеальным генератором, 3. Составьте уравнение электрического равновесия цепи синусоидального тока 4. Запишите выражение мгновенного тока в цепи, приняв начальную фазу равной нулю. 5. Получите выражение мгновенного напряжения на зажимах цепи, подставив 6. Постройте векторную диаграмму тока и напряжений цепи 7. Запишите выражение мгновенного напряжения на зажимах цепи, 8. Получите из векторной диаграммы и постройте треугольник 9. Что понимается под активной составляющей напряжения цепи? 10. Что понимается под реактивной составляющей напряжения цепи? 11. Преобразуйте треугольник напряжений в треугольник сопротивлений, 12. Что понимается под реактивным сопротивлением цепи? 13. Установите связь между параметрами цепи, используя треугольник сопротивлений. 14. Как рассчитать угол сдвига фаз цепи с помощью её параметров? 15. Получите из треугольника сопротивлений треугольник мощностей и постройте его. 16. Что понимается под реактивной мощностью цепи? Какой она может носить характер? 17. Установите связь между мощностями в цепи, используя треугольник мощностей. 18. Дайте определение коэффициента мощности цепи. 19. Запишите и расшифруйте определяющую формулу коэффициента мощности цепи. 20. Как рассчитать коэффициент мощности цепи с помощью её параметров? Задания для самоконтроля К источнику синусоидального напряжения u = 141sin (wt + 30°) В подключены последовательно соединённые катушка и конденсатор. 1. Определить реактивное сопротивление цепи. 2. Определить полное сопротивление цепи. 3. Определить угол сдвига фаз цепи. 4. Определить амплитуду тока в цепи. 5. Записать выражение мгновенного тока в цепи. 6. Определить амплитуду напряжения на активном сопротивлении цепи. 7. Записать выражение мгновенного напряжения на активном сопротивлении цепи. 8. Определить амплитуду напряжения на индуктивности цепи. 9. Записать выражение мгновенного напряжения на индуктивности цепи. 10. Определить амплитуду напряжения на ёмкости цепи. 11. Записать выражение мгновенного напряжения на ёмкости цепи. 1. Найти действующее значение тока в цепи. 2. Найти действующее значение напряжения на зажимах цепи. 3. Найти действующее значение напряжения на активном сопротивлении цепи. 4. Найти действующее значение напряжения на индуктивности цепи. 5. Найти действующее значение напряжения на ёмкости цепи. 6. Найти активную мощность цепи. 7. Найти реактивную мощность индуктивности цепи. 8. Найти реактивную мощность ёмкости цепи. 9. Найти реактивную мощность цепи. 10. Найти полную мощность цепи. 11. Найти коэффициент мощности цепи.
Резонанс напряжений
Рассмотрим расчётную схему цепи переменного синусоидального тока
Полное сопротивление цепи
Рассмотрим режим работы цепи в случае, если хС = хL. Тогда полное сопротивление цепи
Сила тока в цепи
Угол сдвига фаз в цепи будет равен нулю, т.е. j = 0. Цепь будет потреблять только активную мощность
Реактивная мощность
Построим векторную диаграмму тока и напряжений для этого случая (рис.3.39).
Такой режим цепи, когда хс = хL, называется резонансом напряжений. Рассмотрим более подробно условия возникновения резонанса напряжений:
Из (3.124) видно, что резонанса напряжений можно достигнуть, изменяя Введём понятие резонансной частоты, при которой наступает резонанс Находим выражение резонансной частоты из (3.124):
Пример 3.12 К цепи, состоящей из последовательно соединённых Активное сопротивление цепи равно 20 Ом. Индуктивное сопротивление цепи равно 1000 Ом. Емкостное сопротивление цепи равно 1000 Ом. Выполнить анализ цепи. Решение. 1. Определяем полное сопротивление цепи по (3.119): 2. Определяем действующее значение напряжения по (3.16):
3. Определяем действующее значение тока по (3.120):
4. Определяем действующее значение напряжения на активном сопротивлении, используя (3.103): Ur = r×I = 20 × 10 = 200 B. 5. Определяем действующее значение напряжения на индуктивном сопротивлении, используя (3.104): UL = xL×I = 1000×10 = 10000 B. 6. Определяем действующее значение напряжения на емкостном сопротивлении, используя (3.105): Uс = xс×I = 1000×10 = 10000 B. 7. Определяем активную мощность, потребляемую цепью, по (3.121): Р = r×I2 = 20×102 = 2000 Bт. 8. Определяем реактивную мощность, потребляемую цепью, по (3.122): Q = x×I2 = (xL – xс)×I2 = (1000 – 1000)×102 = 0. На основании изложенного можно сформулировать следующие характеристики резонанса напряжений: 1) эквивалентное полное сопротивление цепи 2) угол сдвига фаз цепи равен нулю; 3) цепь потребляет только активную мощность; 4) цепь не потребляет реактивной мощности; 5) приложенное напряжение уравновешивается напряжением 6) напряжение на индуктивности и ёмкости равны между собой 7) между индуктивностью и ёмкостью идет непрерывный обмен энергией: энергия электрического поля конденсатора переходит в энергию Вопросы для самоконтроля 1. Что такое резонанс напряжений? 2. Запишите условия возникновения резонанса напряжений. 3. Что такое резонансная частота? Как её рассчитать с помощью параметров цепи? 4. Дайте характеристику режиму резонанса напряжений. 5. Укажите негативные последствия резонанса напряжений. Задания для самоконтроля К источнику синусоидального напряженияподключены 1. Определить резонансную частоту для этой цепи. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 .
.

 ;
;
 ;
; .
.

 ,
,
 .
.
 .
.
 ,
,
 Если xL> xc , то реактивное сопротивление цепи будет носить индуктивный характер, если xL< xc , то реактивное сопротивление цепи будет носить ёмкостной характер, т.е. в первом случае эквивалентной схемой цепи (расчётной) будет следующая (рис.3.34):
Если xL> xc , то реактивное сопротивление цепи будет носить индуктивный характер, если xL< xc , то реактивное сопротивление цепи будет носить ёмкостной характер, т.е. в первом случае эквивалентной схемой цепи (расчётной) будет следующая (рис.3.34): Во втором случае эквивалентная расчётная схема цепи будет иметь следующий вид (рис.3.35):
Во втором случае эквивалентная расчётная схема цепи будет иметь следующий вид (рис.3.35):
 .
.
 ,
,
 .
.
 В данном случае:
В данном случае: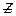 I2, ва.
I2, ва.
 .
.
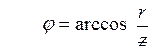 .
.
 .
. .
. .
. .
. .
.
 .
.
 .
.

 .
.



 .
. .
. .
.