
|
|
С резистором и конденсаторомВключим последовательно резистор и конденсатор в цепь переменного синусоидального тока (рис.3.24).
Г – генератор; рА – амперметр; R – резистор; С – конденсатор. Составим расчётную схему цепи (рис.3.25). Зададимся током в цепи
и найдём, каким должно быть в этом случае приложенное напряжение, для чего запишем уравнение электрического равновесия цепи по второму закону Кирхгофа для мгновенных значений:
В соответствии с (3.22) и (3.52) получаем:
Подставляем значение тока (3.80) и получаем:
Запишем мгновенное приложенное напряжение:
Таким образом, в данной цепи приложенное напряжение отстает от тока на угол сдвига фаз j или наоборот – ток опережает напряжение на угол сдвига фаз j. Рассмотрим треугольник напряжений (рис.3.27).
где r – активное сопротивление цепи, Ом; xc – емкостное сопротивление цепи, Ом;
Разделив стороны треугольника напряжений на Im, получим треугольник
Запишем полное сопротивление цепи:
Запишем закон Ома для максимальных и действующих значений тока и
Запишем мощности:
Коэффициент мощности как отношение активной мощности к полной:
Угол сдвига фаз по параметрам цепи может быть найден следующим образом:
Пример 3.10 К цепи, состоящей из последовательно соединённых резистора и конденсатора, подведено напряжение u = 141 sin (wt –30°) В. Активное сопротивление цепи равно 8 Ом. Реактивное сопротивление цепи равно 6 Ом. Выполнить анализ цепи. Решение. 1. Определяем полное сопротивление цепи по (3.92): 2. Определяем амплитуду тока по (3.93):
3. Определяем угол сдвига фаз цепи по (3.99):
4. Определяем начальную фазу тока: yi = yu + j = –30 + 37 = 7°. 5. Записываем мгновенный ток: i = 14,1 sin (wt +7°) А. 6. Определяем амплитуду напряжения на активном сопротивлении по (3.89): Urm = 8×14,1 = 112,8 В. 7. Определяем начальную фазу напряжения на активном сопротивлении: yur = yi= 7°. 8. Записываем мгновенное напряжение на активном сопротивлении: ur = 112,8 sin (wt +7°) В. 9. Определяем амплитуду напряжения на емкостном сопротивлении по (3.90): Uсm = 6×14,1 = 84,6 В. 10. Определяем начальную фазу напряжения на емкостном сопротивлении: yuс = yi– 90 = 7 – 90 = –83°. 11. Записываем мгновенное напряжение на емкостном сопротивлении: uс = 84,6 sin (wt – 83°) В. 12. Определяем действующее значение тока по (3.14):
13. Определяем активную мощность, потребляемую цепью, по (3.95): Р = 8×102 = 800 Вт = 0,8 кВт. 14. Определяем реактивную мощность, потребляемую цепью, по (3.96): Qс = 6×102 = 600 вар = 0,6 квар. 15. Определяем полную мощность, потребляемую цепью, по (3.97): S = 10×102 = 1000 ва = 1,0 ква. 16. Определяем коэффициент мощности цепи по (3.98):
Вопросы для самоконтроля 1. Опишите физические явления, наблюдаемые в реальном конденсаторе 2. Составьте расчётную схему цепи с идеальным генератором и реальным конденсатором. 3. Составьте уравнение электрического равновесия цепи синусоидального тока 4. Запишите выражение мгновенного тока в цепи, приняв начальную фазу равной нулю. 5. Получите выражение мгновенного напряжения на зажимах цепи, подставив 6. Постройте векторную диаграмму тока и напряжений цепи 7. Запишите выражение мгновенного напряжения на зажимах цепи, 8. Получите из векторной диаграммы и постройте треугольник 9. Преобразуйте треугольник напряжений в треугольник сопротивлений, 10. Установите связь между параметрами реального конденсатора, 11. Как рассчитать угол сдвига фаз реального конденсатора с помощью его параметров? 12. Получите из треугольника сопротивлений треугольник мощностей и постройте его. 13. Установите связь между мощностями реального конденсатора, 14. Дайте определение коэффициента мощности реального конденсатора. 15. Запишите и расшифруйте определяющую формулу коэффициента мощности
Задания для самоконтроля К источнику синусоидального напряжения u = 282sin (wt + 47°) В подключены последовательно соединённые резистор и конденсатор. 1. Найти полное сопротивление цепи. 2. Найти угол сдвига фаз цепи. 3. Найти амплитуду тока в цепи. 4. Записать мгновенное значение тока в цепи. 5. Найти амплитуду напряжения на активном сопротивлении. 6. Записать мгновенное значение напряжения на активном сопротивлении. 7. Найти амплитуду напряжения на ёмкости. 8. Записать мгновенное значение напряжения на ёмкости. 9. Построить векторную диаграмму напряжений и тока цепи. 10. Найти активную мощность цепи. 11. Найти реактивную мощность цепи. 12. Найти полную мощность цепи. 13. Найти коэффициент мощности цепи.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



 ,
,
 ,
,
 .
.
 .
.
 ,
где Urm = rIm,
Ucm = xcIm.
,
где Urm = rIm,
Ucm = xcIm.
 Построим векторную диаграмму тока и напряжений этой цепи (рис.3.26).
Построим векторную диаграмму тока и напряжений этой цепи (рис.3.26). ,
т.к. yi = 0.
,
т.к. yi = 0.
 Запишем выражения сторон треугольника:
Запишем выражения сторон треугольника: ,
,
 ,
,
 ,
,
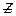 – полное сопротивление цепи, Ом.
– полное сопротивление цепи, Ом.
 .
.
 ;
;
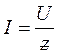 .
.
 Умножим стороны треугольника сопротивлений на квадрат действующего
Умножим стороны треугольника сопротивлений на квадрат действующего  .
.
 .
.
 .
. .
. .
. .
. .
.