
|
|
Симплекс–метод решения задач линейного программированияБудем рассматривать задачу линейного программирования в канонической форме (2.1)-(2.3). Выразим целевую функцию через свободные переменные:
или
где
Задачу линейного программирования можно компактно записать с помощью, так называемой симплекс-таблицы. Строке с номером
а в последней строке записаны симплекс-разности Таблица 2.1 Общий вид симплекс таблицы
Теорема 3. Если все симплексные разности Теорема 4. Если среди отрицательных симплексных разностей Теорема 5. Об улучшении плана. Пусть Таким образом, если в точке Таким образом, симплекс-метод представляет собой направленный перебор допустимых базисных решений (угловых точек допустимого множества) задачи линейного программирования с последовательным увеличением целевой функции. Условия разрешимости задачи линейного программирования симплекс-методом: 1. Канонический вид задачи линейного программирования. 2. Все коэффициенты правых частей системы ограничений неотрицательны ( 3. Наличие базиса, то есть среди векторов
Алгоритм симплекс-метода Шаг 1. Составляем симплекс-таблицу и рассчитываем симплекс-разности Шаг 2. Определяем знак симплекс-разностей: · если все · если существуют Шаг 3. Определяем ключевой столбец. Ключевым или разрешающим столбцом называется столбец соответствующий максимальной по модулю Шаг 4. Определяем знак элементов ключевого столбца: · если все · если Шаг 5. Определяем ключевую строку. Ключевой строкой называется строка, в которой отношение Шаг 6. Переходим к новой симплекс-таблице и новому базису, выводя из него неизвестный
Переходим к шагу 1. Замечание: 1. Если 2. Если исходная задача линейного программирования является вырожденной, то есть среди ее всевозможных базисных решений есть вырожденные, то в ходе ее решения симплекс-методом могут появиться и вырожденные базисные решения. При этом возможны холостые шаги симплекс-метода, т.е. итерации, на которых Однако в подавляющем большинстве случаев холостые шаги сменяются шагами с убыванием целевой функции и процесс решения завершается в результате конечного числа итераций.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (2.6)
(2.6) , (2.7)
, (2.7) ,
,  – исходный план задачи (2.1)-(2.3),
– исходный план задачи (2.1)-(2.3),  ,
, 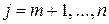 – симплекс-разности, которые рассчитываются по следующей формуле:
– симплекс-разности, которые рассчитываются по следующей формуле: ,
,  этой таблицы соответствует
этой таблицы соответствует  ,
,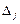 целевой функции в точке
целевой функции в точке 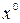 .
.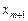


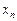
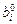







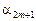
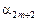


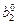






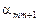

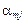
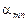



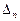

 , то в точке
, то в точке 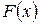 на допустимом множестве
на допустимом множестве  .
.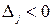 ,
, 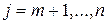 есть такая разность, например
есть такая разность, например  , что все
, что все 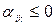 , то максимум целевой функции
, то максимум целевой функции  не достигается.
не достигается. является невырожденным допустимым базисным решением задачи (2.1)-(2.3), т.е.
является невырожденным допустимым базисным решением задачи (2.1)-(2.3), т.е. 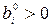 ,
, 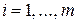 . Тогда, если хотя бы одна из симплексных разностей
. Тогда, если хотя бы одна из симплексных разностей  ,
,  , например
, например  есть положительные, то существует допустимое базисное решение
есть положительные, то существует допустимое базисное решение  , для которого
, для которого  .
.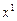 , для которого
, для которого  , то случай, описанный в теореме 5, может повторяться лишь конечное число раз. Поэтому в результате конечного числа шагов перехода к новому допустимому базисному решению задача будет решена или будет установлена ее неразрешимость.
, то случай, описанный в теореме 5, может повторяться лишь конечное число раз. Поэтому в результате конечного числа шагов перехода к новому допустимому базисному решению задача будет решена или будет установлена ее неразрешимость.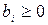 ,
,  ).
). ,
,  должно быть
должно быть 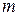 единичных.
единичных. по формуле (2.8).
по формуле (2.8). ,
, 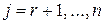 , то получен оптимальный план;
, то получен оптимальный план; ,
,  среди отрицательных симплекс-разностей.
среди отрицательных симплекс-разностей. ,
,  то
то  );
); ,
,  минимально при условии, что
минимально при условии, что  , строка с номером
, строка с номером 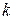 называется ключевой (разрешающей), а элемент
называется ключевой (разрешающей), а элемент 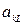 – ключевой элемент.
– ключевой элемент.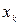 , заменяя его на известный
, заменяя его на известный 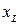 . Изменение базиса означает переход к новому плану. Элементы новой симплекс-таблицы вычисляются следующим образом:
. Изменение базиса означает переход к новому плану. Элементы новой симплекс-таблицы вычисляются следующим образом: ,
, 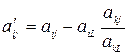 .
.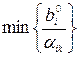 выполняется в нескольких точках, то в качестве ключевого элемента можно выбрать любой из них.
выполняется в нескольких точках, то в качестве ключевого элемента можно выбрать любой из них.