Теоретические основы оптимизации по симплекс-методу

Поиск оптимального решения сводится к задаче линейного программирования. Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

Каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника

Алгоритм решения Симплекс-методом оптимизационной задачи линейного программирования осуществляется путём перебора вершин выпуклого многогранника в многомерном пространстве. Методика линейного программирования была разработана Д. Данцигом в 1947 году.

Идея симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.

Последовательность вычислений симплекс-методом можно разделить на два этапа:

1) нахождение исходной вершины множества допустимых решений,

2) последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, не всегда, далеко не оптимальным).

Симплекс-метод является универсальным, то есть может быть использован при любом количестве независимых переменных. Симплекс-метод реализуется путём перехода от одной вершины пространственного многогранника к другой при условии, что значение целевой функции должно увеличиваться или не уменьшаться.

Для реализации симплекс-метода необходимо перевести систему ограничений из стандартной формы в каноническую, то есть преобразовать ограничения в виде неравенств в ограничения в форме равенств.

В качестве задачи многомерной оптимизации будем рассматривать задачу линейного программирования в канонической форме:

, (2.1)

, (2.2)

, (2.3)

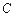где – вектор коэффициентов целевой функции; – вектор управляющих переменных; 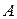– матрица коэффициентов системы ограничений, имеющая размерность и .

Имеем независимых переменных, которые назовем свободными, остальные – зависимые или базисные. Выразим базисные переменные через свободные:

, , (2.4)

где – компоненты вектора после элементарных преобразований матрицы . Формула (2.4) является решением системы уравнений (2.2). При этом, если , тогда – базисное решение задачи (2.1)-(2.3), если все , .

Будем полагать, что , тогда каждому выбору 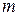базисных переменных системы (2.2) соответствует свое базисное решение. Поэтому число базисных решений равно числу всевозможных базисных миноров матрицы , но не превосходит .

Допустим множество задачи (2.1)-(2.3) представляет собой выпуклый многогранник в пространстве . И любую его внутреннюю точку можно представить в виде линейной комбинации угловых точек множества :

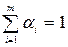, . (2.5)

Теорема 1. Базисное решение задачи (2.1)-(2.3) является угловой точкой области допустимых решений .

Теорема 2. Об оптимальном решении. Пусть – множество допустимых решений не пустое ограниченное множество. Тогда существует оптимальное решение задачи (2.1)-(2.3) и оно достигается в одной из угловых точек множества допустимых решений.

Не нашли, что искали? Воспользуйтесь поиском по сайту: