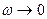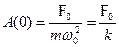|
|
Указания по технике безопасностиОсторожно обращайтесь с оборотным маятником. Не допускайте падений и ударов маятника, это может нарушить его регулировку. Лабораторная работа №3 Свободные колебания в RLC контуре
Цель работы: * Знакомство с моделью свободных колебаний в последовательном RLC-контуре. * Экспериментальное исследование закономерностей свободных незатухающих и затухающих колебаний. * Экспериментальное определение характеристик затухания в RLC-контуре. Основные понятия: В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
где
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
Здесь принято обозначение: В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону q(t) = q0cos(ωt + φ0) (4) Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
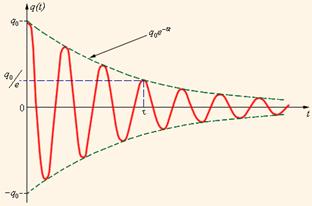
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рисунок 2).
Рисунок 2 Затухающие колебания Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – dυ. Коэффициент d в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
где Скорость затухания зависит от электрического сопротивления R контура. Интервал времени в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания. Для характеристики степени затухания в контуре, кроме величины δ, вводят понятие логарифмического декремента затухания q. Он равен натуральному логарифму отношения двух последующих амплитуд (отстоящих во времени на один период)
Добротность Q колебательной системы вычисляется:
Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
Для RLC-контура добротность Q выражается формулой
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен. Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω0 идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь. Расчетные формулы:
добротность RLC-контура:
Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Свободные колебания в RLC-контуре». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.
Нажмите кнопку «Старт».Пронаблюдайте картину затухающих колебаний в RLC-контуре. Установите значение R=0. Пронаблюдайте картину незатухающих колебаний. Получите у преподавателя допуск для выполнения измерений. Порядок измерений и обработка результатов: ЭКСПЕРИМЕНТ 1. Определение периода затухающих и незатухающих колебаний.
ТАБЛИЦА 1. Параметры RLC-контура (не перерисовывать)
ТАБЛИЦА 2. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=0 Ом.
ТАБЛИЦА 3. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=____ Ом.
t =____с, ЭКСПЕРИМЕНТ 2 Определение логарифмического декремента затухания.
ТАБЛИЦА 4. Логарифмический декремент затухания
ЭКСПЕРИМЕНТ 3 Определение добротности контура.
ТАБЛИЦА 5. Добротность контура
Лабораторная работа №4 Вынужденные колебания Цель работы: Знакомство с компьютерной моделью вынужденных механических колебаний. Экспериментальное исследование амплитудно-частотной характеристики пружинного маятника.
Основные понятия: Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения. Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0. Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы. После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе. В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы. Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила y = ym cos ωt, где ym – амплитуда колебаний, ω – круговая частота. Такой закон перемещения можно обеспечить с помощью шатунного механизма, не показанного на рисунке 1.
Рисунок 1. Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно: Δl = x – y = x – ym cos ωt. Второй закон Ньютона для тела массой m: ma = –k(x – y) = –kx + kym cos ωt. В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой. Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: Тогда уравнение вынужденных колебаний запишется в виде
где
Это уравнение не учитывает действия сил трения. С учетом сил трения уравнение вынужденных колебаний имеет вид:
где Решение этого дифференциального уравнения состоит из двух частей: общего решения и частного решения:
где первое слагаемое отвечает собственным затухающим колебаниям, а второе – вынужденным. Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону x(t) = А(w)cos (ωt + j). Можно показать, что xm и j зависят от ω следующим образом:
Амплитуда вынужденных колебаний при
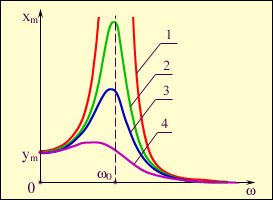
На очень низких частотах, когда ω << ω0, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом x(t) = y(t), и пружина остается практически недеформированной. Внешняя сила Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой (рисунок 2). При резонансе амплитуда xm колебания груза может во много раз превосходить амплитуду ym колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе. У колебательных систем с не очень высокой добротностью (< 10) резонансная частота несколько смещается в сторону низких частот. Это хорошо заметно на рисунке 2.
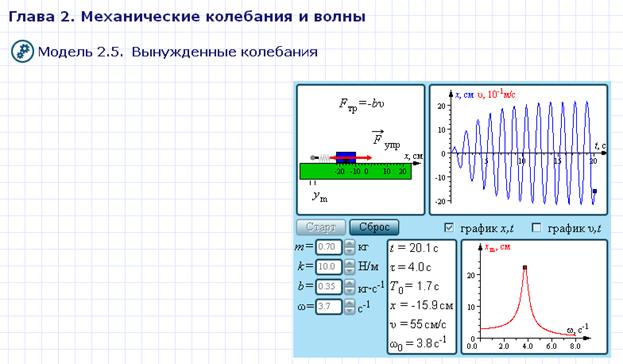
Рисунок 2. Амплитудно-частотная характеристика Резонансные кривые при различных уровнях затухания: 1 – колебательная система без трения; при резонансе амплитуда xm вынужденных колебаний неограниченно возрастает; 2, 3, 4 – реальные резонансные кривые для колебательных систем с различной добротностью: Q2 > Q3 > Q4. На низких частотах (ω << ω0) xm ≈ ym. На высоких частотах (ω >> ω0) xm → 0. Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Вынужденные колебания». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.
Обратите внимание, что в данной работе коэффициент вязкого трения r обозначен как b. Установите флажок к графику x,t и v,t. Нажмите кнопку «Старт». Пронаблюдайте картину вынужденных колебаний пружинного маятника, изменяя параметры колебательной системы. Обратите внимание на то, что установившиеся вынужденные колебания всегда происходят на частоте вынуждающей силы. Получите у преподавателя допуск для выполнения измерений. Порядок измерений и обработка результатов: ЭКСПЕРИМЕНТ 1. Определение резонансной частоты колебательной системы.
ТАБЛИЦА 1. Параметры колебательной системы (не перерисовывать)
ТАБЛИЦА 2. Результаты измерений при m= ____ кг, k = ____ Н/м. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (1)
(1)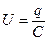 – напряжение на конденсаторе, q – заряд конденсатора,
– напряжение на конденсаторе, q – заряд конденсатора,  – ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t):
– ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t): (2)
(2) (3)
(3) Уравнение (3) описывает свободные колебания в LC-контуре в отсутствие затухания.
Уравнение (3) описывает свободные колебания в LC-контуре в отсутствие затухания.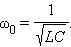 (5)
(5) (6)
(6)
 (7)
(7) , (8),
, (8), -амплитуда затухающих колебаний,
-амплитуда затухающих колебаний,  - начальная амплитуда.
- начальная амплитуда. , (9)
, (9) , (10)
, (10)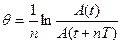 , (11)
, (11) . (12)
. (12)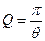
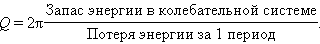
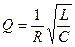
 - период незатухающих колебаний,
- период незатухающих колебаний, - период затухающих колебаний,
- период затухающих колебаний,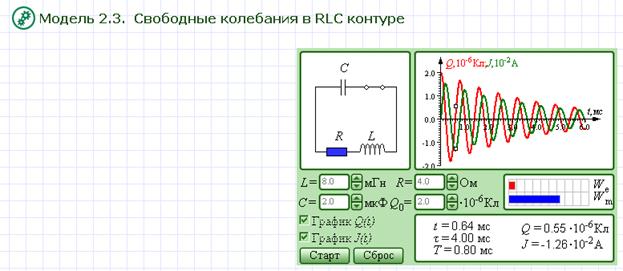
 для каждого значения n. Вычислите среднее значение периода.
для каждого значения n. Вычислите среднее значение периода. , с
, с
 . Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний
. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний  .
. .
. =
= 
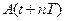
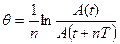
 .
. .
. и добротность
и добротность 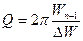
 .
.
 приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону
приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону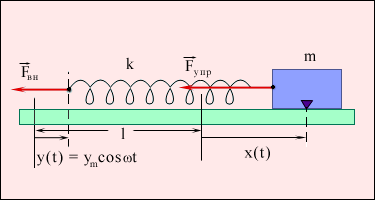
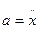
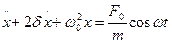
 – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина
– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина  определяется выражением:
определяется выражением: .
. - коэффициент затухания.
- коэффициент затухания. ,
, ,
, .
.